Скінченний автомат

Скінче́нний автома́т (англ. finite-state machine, автомат зі скінченною множиною станів) — модель що використовується для опису зміни стану об'єкта в залежності від поточного стану та інформації отриманої ззовні. Поняття скінченного автомата було запропоновано як математичну модель дискретних приладів, оскільки будь-який такий прилад (через скінченність своїх розмірів) може мати тільки скінченну кількість станів.
Скінченні автомати допомагають розв'язувати багато задач, серед яких автоматизація проєктування електронних приладів, проєктування комунікаційних протоколів, синтаксичний аналіз та інші інженерні застосування. В біології і дослідженнях штучного інтелекту, автомати або їх ієрархії іноді використовуються для опису неврологічних систем і в лінгвістиці для опису граматики природних мов.
Класифікація[ред. | ред. код]
Існує дві різних групи автоматів: Акцептори/Розпізнавачі і Перетворювачі (Трансдуктори).
Акцептори і розпізнавачі[ред. | ред. код]
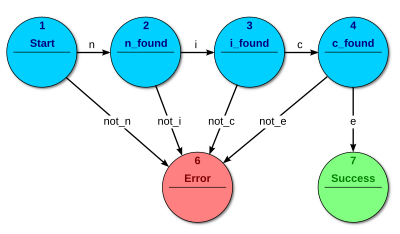
Акцептори і розпізнавачі (також виявлювачі послідовностей) дають двійковий результат, відповідаючи так або ні на питання чи вхідні дані приймаються автоматом. Всі стани автомата можуть бути або приймаючими або ні. Якщо поточний стан автомата є приймаючим, значить послідовність подана на вхід приймається. Як правило, на вхід подаються символи (літери); дії не виконуються. Приклад на зображенні показує автомат, який приймає слово «nice». В цьому автоматі єдиний допустимий стан це 7.
Автомат також може бути описаний як такий, що визначає мову, яка містить всі слова розпізнавані цим автоматом, але не ті які ним відхиляються; тоді ми кажемо, що ця мова розпізнається автоматом. За визначенням, мови розпізнавані СА це регулярні мови, тобто мова є регулярною якщо існує деякий СА, який розпізнає її.
Початковий стан[ред. | ред. код]
Початковий стан зазвичай позначається стрілкою «звідкись».
Допустимі (або кінцеві) стани[ред. | ред. код]

Допустимі стани (також відомі як кінцеві стани) це такі, що якщо автомат знаходиться в них це означає, що вхідний рядок, наскільки він опрацьований, належить мові що розпізнається. Зазвичай позначається двома колами.
Приклад допустимого стану з'являється в діаграмі праворуч: a детермінований скінченний автомат (ДСА), що визначає чи двійковий вхідний рядок містить парну кількість 0.
S1 (який є початковим станом) показує стан в якому парна кількість 0 була введена. Цей автомат опиниться в допустимому стані, якщо двійковий рядок містить парну кількість 0 (включно з рядком, що не містить 0 взагалі). Приклади рядків розпізнаваних цим ДСА це порожній рядок, 1, 11, 11…, 00, 010, 1010, 10110, і подібні …
Перетворювачі (Трансдуктори)[ред. | ред. код]
Перетворювачі продукують вихід або виконують інші дії, на основі символу на вході і/або на станах. Вони використовуються для керування і в галузі математичної лінгвістики. Тут вирізняють два типи:
- Автомат Мура
- вихід залежить тільки від стану. Перевагою моделі Мура є спрощення поведінки. Уявімо двері підйомника. Автомат розпізнає дві команди: «відчинити» і «зачинити», які викликають зміну стану. Вхідна дія (E:) в стані «Відчиняються» змушує двигун відчиняти двері, вхідна дія в стані «Зачиняються» змушує двигун зачиняти двері. Стани Відчинено і Зачинено зупиняють мотор коли двері повністю відчинені або зачинені. Вони повідомляють зовнішній світ (наприклад, інші автомати) про ситуацію: «двері відчинені» або «двері зачинені».

- Автомат Мілі
- вихід залежить від входу і стану. Використання скінченного автомата Мілі часто призводить до зменшення кількості станів. Приклад на схемі показує скінченний автомат Мілі, який має однакову поведінку із прикладом автомата Мура. Присутні дві вхідні дії (I:): «запустити двигун для закриття дверей якщо прийшла команда зачинити» і «запустити мотор в іншому напрямку якщо для відчинення дверей якщо прийшла команда відчинити». Проміжні стани «Відчинення» і «Зачинення» не показані.
На практиці часто використовується суміш моделей.[1]
Детермінованість[ред. | ред. код]
Подальша відмінність між Детермінованими (ДСкА) і недетермінованими (НДСкА) автоматами. В детермінованих автоматах, кожен стан має один перехід для кожного входу. В недетермінованих автоматах вхід може призвести до одного, більше ніж одного або жодного переходу для даного стану. Ця різниця важлива на практиці, але не в теорії, через існування алгоритму трансформації будь-якого НДСкА в складніший ДСкА з аналогічною функціональністю.
Якщо автомат має лише один стан, то, згідно Енциклопедії кібернетики він називається автоматом без пам'яті ((англ. combinatorial finite-state machine). Оскільки під час роботи стан такого автомату змінюватись не може, то вихідний символ залежить саме від вхідного символу в поточному такті, і не залежить від символів, які надходили перед тим. Оператор, який реалізується таким автоматом, виконує перетворення літери за літерою вхідних символів у вихідні.
Математична модель[ред. | ред. код]
Згідно із загальною класифікацією, дані наступні визначення:
- детермінований скінченний автомат або детермінований скінченний автомат акцептор є п'ятіркою , де:
- вхідна абетка (скінченний, не порожній набір символів).
- — скінченний, не порожній набір станів.
- — початковий стан, елемент з .
- — функція переходу: (в недетермінованих скінченних автоматах це буде , тобто, повертає набір станів).
- набір кінцевих станів, (можливо порожня) підмножина .
Для обох детермінованих і недетермінованих СА, зручно дозволити бути неповною функцією, тобто не має бути визначеною для кожної комбінації і . Якщо СА перебуває в стані , наступний символ і не визначена, тоді може повідомити про помилку (тобто відхілити ввід).
- скінченний перетворювач це шістка , де:
- — вхідна абетка (скінченний, не порожній набір символів).
- — вихідна абетка (скінченний, не порожній набір символів).
- — скінченний, не порожній набір станів.
- — початковий стан, елемент з (в недетермінованих скінченних автоматах, це набір початкових станів).
- — функція переходу: .
- функція виходу.
Якщо функція виходу є функцією стану і вхідної абетки() таке визначення відповідає моделі Мілі, і може бути виконана як автомат Мілі. Якщо функція виходу залежить тільки від стану () тоді таке визначення відповідає моделі Мура, і може бути виконана як автомат Мура. Скінченний автомат без функції виходу відомий як напівавтомат або як модель станів і переходів.
Автоматні оператори[ред. | ред. код]
Означення: Відповідність, яка відображає вхідні ланцюжки a автомата M у вихідні ланцюжки w називають автоматним відображенням, а також автоматним оператором M. Якщо результат застосування цього оператора до ланцюжка a — вихідний ланцюжок w,
то це позначають M(a) = w. Кількість символів у ланцюжку a, як завжди, називають довжиною ланцюжка a та позначають |a| чи l(a).
Автоматне відображення має дві властивості:
1. Ланцюжки a та w = M(a) мають однакову довжину: |a| = |w| (збереження довжини).
2. Якщо a = a1a2 й M(a1a2) = w1w2, де |a1| = |w1|, то M(a1) = w1, тобто образ відрізка довжиною l дорівнює відрізку образу з такою самою довжиною.
Властивість 2 означає, що автоматні оператори — це оператори без випередження, тобто такі, котрі, обробляючи ланцюжок зліва направо, «не підглядають уперед»: i-та буква вихідного ланцюжка залежить тільки від перших i букв вхідного ланцюжка. Приклад оператора з випередженням — той, який ланцюжку a = x1x2…xk ставить у відповідність ланцюжок xk…x1x2, перша буква вихідного ланцюжка тут дорівнює останній букві вхідного ланцюжка. Зазначимо, що ці дві властивості — це не достатні умови автоматності відображення: існують відображення, які задовольняють умови 1 і 2, але не реалізовані в скінченному автоматі.
Див. також[ред. | ред. код]
Примітки[ред. | ред. код]
- ↑ Moore or Mealy model: that's the question. www.stateworks.com. Процитовано 8 вересня 2023.
| Ця стаття містить перелік посилань, але походження окремих тверджень залишається незрозумілим через брак внутрішньотекстових джерел-виносок. (вересень 2021) |
Посилання[ред. | ред. код]
Українською[ред. | ред. код]
- Гаврилків В. М. Формальні мови та алгоритмічні моделі. — І.-Ф. : Голіней, 2023. — 180 с.
Іншими мовами[ред. | ред. код]
- Серебряков В. А., Галочкин М. П., Гончар Д. Р., Фуругян М. Г. Теория и реализация языков программирования [Архівовано 3 січня 2022 у Wayback Machine.] — М.: МЗ-Пресс, 2006 г., 2-е изд. — ISBN 5-94073-094-9
- Теория автоматов / Э. А. Якубайтис, В. О. Васюкевич, А. Ю. Гобземис, Н. Е. Зазнова, А. А. Курмит, А. А. Лоренц, А. Ф. Петренко, В. П. Чапенко // Теория вероятностей. Математическая статистика. Теоретическая кибернетика. — М.: ВИНИТИ, 1976. — Т. 13. — С. 109—188. — URL http://www.mathnet.ru/php/getFT.phtml?jrnid=intv&paperid=28&what=fullt&option_lang=rus
- Применение конечных автоматов для решения задач автоматизации [Архівовано 12 вересня 2021 у Wayback Machine.]
- Глушков В. М. Синтез цифровых автоматов. — М.: ГИФМЛ[ru], 1962. — 476 с.
| Це незавершена стаття з інформатики. Ви можете допомогти проєкту, виправивши або дописавши її. |
| Це незавершена стаття з математики. Ви можете допомогти проєкту, виправивши або дописавши її. |
| |||||||||||||||||||



















