Конфігурація (геометрія)

Конфігурації (4₃6₂₎ (повний чотирикутник, ліворуч) і (6₂4₃₎ (повний чотирибічник, праворуч)

У проєктивній геометрії конфігурація на площині складається зі скінченної множини точок і скінченної конфігурації прямих, таких, що кожна точка інцидентна однаковому числу прямих і кожна пряма інцидентна однаковому числу точок.

Хоча деякі специфічні конфігурації вивчалися раніше (наприклад, Томасом Кіркманом 1849 року), формальне вивчення конфігурацій почав уперше Теодор Реє 1876 року в другому виданні його книги Geometrie der Lage (Геометрія положення), в контексті обговорення теореми Дезарга. Ернст Штайніц написав дисертацію на цю тему 1894 року і конфігурації популяризували 1932 року Гільберт і Кон-Фоссен у книзі Anschauliche Geometrie (Наочна геометрія), перекладеній англійською і російською мовами.

Конфігурації можна вивчати або як конкретні множини точок і прямих у конкретній геометрії, наприклад, на евклідовій або проєктивній площині (в цьому випадку кажуть про реалізацію в цій геометрії), або як абстрактну геометрію інцидентності. В останньому випадку конфігурації тісно пов'язані з регулярними гіперграфами і бірегулярними двочастковими графами, але з додатковим обмеженням — будь-які дві точки структури інцидентності можуть асоціюватися максимум з однією прямою, а будь-які дві прямі можуть асоціюватися максимум з однією точкою. Тобто обхват відповідного двочасткового графу (графу Леві конфігурації) має дорівнювати щонайменше шести.

Позначення

Конфігурація на площині позначається як (p_γ ℓ_π), де p — число точок, ℓ — число прямих, γ — число прямих, що проходять через кожну точку, а π — число точок на кожній прямій. Для цих чисел має виконуватися співвідношення

$p\gamma =\ell \pi$,

оскільки цей добуток дорівнює числу інціденцій точка-пряма (прапорів).

Конфігурації з тим самим символом не зобов'язані бути ізоморфними як структури інцидентності. Наприклад, існує три різних конфігурації (9₃ 9₃₎ — конфігурація Паппа і дві менш відомі конфігурації.

У деяких конфігураціях p = ℓ, а тому, γ = π. Вони називаються симетричними або збалансованими конфігураціями і зазвичай у позначеннях повторення опускають. Наприклад, (9₃ 9₃₎ скорочується до (9₃).

Приклади

Конфігурація (10₃), не ізоморфна за інцидентністю конфігурації Дезарга

Найвідоміші такі проєктивні конфігурації:

• (1₁), найпростіша можлива конфігурація, що складається з точки на прямій. З огляду на тривіальність часто не розглядається.
• (3_2), трикутник. Кожна з трьох сторін містить дві з трьох вершин, і навпаки. Узагальнено, будь-який багатокутник з n сторонами утворює конфігурацію типу (n₂).
• (4₃ 6₂) і (6₂ 4₃), повний чотирикутник і повний чотирибічник відповідно.
• (7₃), площина Фано. Ця конфігурація існує як абстрактна геометрія інцидентності, але її не можна побудувати на евклідовій площині.
• (8₃), конфігурація Мебіуса — Кантора. Ця конфігурація складається з двох чотирикутників, одночасно описаних і вписаних відносно один одного. Конфігурацію можна побудувати на евклідовій площині, але рівняння, що її визначають, мають нетривіальні розв'язки в комплексних числах.
• (9₃), конфігурація Паппа.
• (9₄ 12₃), конфігурація Гессе дев'яти точок перегину кубики на комплексній проєктивній площині і дванадцяти прямих, кожна з яких містить по три точки. Ця конфігурація має ту ж властивість, що й площина Фано, а саме, вона містить усі прямі, що проходять через будь-які дві точки конфігурації. Конфігурації з такими властивостями відомі як конфігурації Сильвестра — Галлаї. Ці конфігурації за теоремою Сильвестра не можна реалізувати в дійсній площині.
• (10₃), конфігурація Дезарга.
• (12₅ 30₂), подвійна шістка Шлефлі, утворена 12 прямими з 27 прямих на кубічній поверхні.
• (15₃), конфігурація Кремони — Річмонда, утворена 15 прямими, що не входять у подвійну шістку, і відповідними 15 дотичними площинами.
• (12₄ 16₃), конфігурація Реє.
• (16₆), конфігурація Куммера.
• (27_3), конфігурація Грея.
• (60₁₅), конфігурація Кляйна.

Двоїстість конфігурацій

Проєктивно двоїстою конфігурацією для (p_γ l_π) є конфігурація (l_π p_γ), в якій ролі «точок» і «прямих» міняються місцями. Тому конфігурації йдуть двоїстими парами, за винятком випадків, коли двоїста конфігурація ізоморфна початковій. Ці винятки називають самодвоїстими конфігураціями і в цих випадках p=l.

Число конфігурацій (n₃)

Число неізоморфних конфігурацій типу (n₃), починаючи з n=7, є елементом послідовності

1, 1, 3, 10, 31, 229, 2036, 21399, 245342,... послідовність A001403 з Онлайн енциклопедії послідовностей цілих чисел, OEIS

Ці числа підраховані як абстрактні структури інцидентності, незалежно від можливості їх реалізації. Як пише Гроппа, дев'ять з десяти конфігурацій (10₃) і всі конфігурації (11₃) і (12₃) допускають реалізацію в евклідовому просторі, але для всіх n≥16 є щонайменше одна нереалізовна конфігурація (n₃). Гроппа також вказує на давню помилку в цій послідовності — в статті 1895 року зроблено спробу перелічити всі конфігурації (12₃) і 228 з них знайдено, але 229-а конфігурацію не відкрито аж 1988 року.

Побудова симетричних конфігурацій

Є кілька методів побудови конфігурацій, зазвичай починаючи зі вже відомих конфігурацій. Деякі найпростіші з цих методів будують симетричні (p_γ) конфігурації.

Будь-яка скінченна проєктивна площина порядку n є конфігурацією ((n²+n+1)_n+1)_. Нехай Π — проєктивна площина порядку n. Видалимо з Π точку P і всі прямі Π, що проходять через P (але не точки, що лежать на цих прямих, за винятком точки P) і видалимо пряму l, що не проходить через P, і всі точки, що лежать на цій прямій. Результатом буде конфігурація типу ((n²—1)_n). Якщо при побудові виберемо пряму l, що проходить через P, отримаємо конфігурацію типу ((n²)_n)_. Оскільки відомо, що проєктивні площини існують для всіх порядків n, що є степенями простих чисел, ці побудови забезпечують нескінченне сімейство симетричних конфігурацій.

Не всі конфігурації реалізовні, наприклад, конфігурація (43₇) не існує. Однак Групп дав побудову, яка показує, що для k≥3 конфігурація (p_k) існує для всіх p≥2l_k+1, де l_k — довжина оптимальної лінійки Голомба порядку k.

Високі розмірності

Подвійна шістка Шлефлі

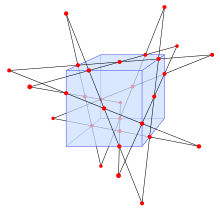
Концепцію конфігурації можна узагальнити на вищі розмірності, наприклад для точок і прямих чи площин у просторі. У цьому випадку обмеження, що ніякі дві точки не можуть лежати більш ніж на одній прямій, можна послабити, оскільки дві точки можуть належати більш ніж одній площині.

У тривимірному просторі цікавими є

• Конфігурація Мебіуса, що складається з двох взаємно вписаних тетраедрів.
• Конфігурація Реє, що складається з дванадцяти точок і дванадцяти площин з шістьма точками на кожній площині і шістьма площинами, що проходять через кожну точку.
• Конфігурація Грея, що складається з 27 точок решітки 3×3×3 і 27 ортогональних прямих, що проходять через них.
• Подвійна шістка Шлефлі, що складається з 30 точок і 12 прямих, по дві прямі на точку і по п'ять точок на одній прямій.

Подальше узагальнення виходить у тривимірному просторі при розгляді інцидентності точок, прямих і площин, тобто j-просторів при 0≤j<3, де кожен j-простір інцидентний N_jk k-просторам (j≠k). Якщо позначити через N_jj число j-просторів, таку конфігурацію можна подати у вигляді матриці:

${\begin{vmatrix}{\begin{vmatrix}N_{00}&N_{01}&N_{02}\\N_{10}&N_{11}&N_{12}\\N_{20}&N_{21}&N_{22}\end{vmatrix}}\end{vmatrix}}$

Підхід можна узагальнювати для інших розмірностей n, де 0≤j<n. Такі зміни математично пов'язані з правильними многогранниками.

Див. також

• Комплексні многогранники (які краще називати комплексними конфігураціями)
• Конфігурація (розбиття простору)

Література

• Leah W. Berman. Movable (n₄) configurations // The Electronic Journal of Combinatorics. — Т. 13, вип. 1. — С. R104..
• A. Betten, G. Brinkmann, T. Pisanski. Counting symmetric configurations // Discrete Applied Mathematics. — 2000. — Т. 99, вип. 1–3 (3 листопада). — С. 331–338. — DOI:10.1016/S0166-218X(99)00143-2..
• H.S.M. Coxeter. Regular Polytopes. — Methuen and Co, 1948..
• H.S.M. Coxeter. Self-dual configurations and regular graphs // The Beauty of Geometry. — Dover. — 1999. — ISBN 0-486-40919-8.
• Peter Dembowski. Finite geometries. — Berlin, New York : Springer-Verlag, 1968. — Т. Band 44. — (Ergebnisse der Mathematik und ihrer Grenzgebiete) — ISBN 3-540-61786-8.
• Harald Gropp. On the existence and non-existence of configurations n_k // Journal of Combinatorics and Information System Science. — 1990. — Т. 15 (3 листопада). — С. 34–48.
• Harald Gropp. Configurations and their realization // Discrete Mathematics. — 1997. — Т. 174, вип. 1–3 (3 листопада). — С. 137–151. — DOI:10.1016/S0012-365X(96)00327-5..
• Branko Grünbaum. The Coxeter Legacy: Reflections and Projections / Chandler Davis, Erich W. Ellers. — American Mathematical Society, 2006. — С. 179–225..
• Branko Grünbaum. Configurations of Points and Lines. — American Mathematical Society, 2009. — Т. 103. — (Graduate Studies in Mathematics) — ISBN 978-0-8218-4308-6..
• David Hilbert, Stephan Cohn-Vossen. Geometry and the Imagination. — 2nd. — Chelsea, 1952. — ISBN 0-8284-1087-9..
• L. M. Kelly. A resolution of the Sylvester–Gallai problem of J. P. Serre // Discrete and Computational Geometry. — 1986. — Т. 1, вип. 1 (3 листопада). — С. 101–104. — DOI:10.1007/BF02187687..
• Tomaž Pisanski, Brigitte Servatius. Configurations from a Graphical Viewpoint. — Springer, 2013. — ISBN 9780817683641..

Посилання

• Weisstein, Eric W. Конфігурація(англ.) на сайті Wolfram MathWorld.