Описаний чотирикутник: відмінності між версіями
| [перевірена версія] | [очікує на перевірку] |
м додано Категорія:Типи чотирикутників за допомогою HotCat |
трошки доповнив)))) |
||
| Рядок 1: | Рядок 1: | ||
{{без джерел|дата=травень 2018}} |
{{без джерел|дата=травень 2018}} |
||
[[Файл:Описаний чотирикутник.png|міні|330x330пкс|Чотирикутник, описаний навколо кола.]] |
|||
[[File:Tangential quadrilateral.svg|150px|thumb|right|Описаний чотирикутник]] |
|||
''' |
В Евклідовій геометрії '''описаний чотирикутник''' {{Sfn|Істер О.С.|2021}}{{rp|cтор.54}} — [[Опуклий многокутник|опуклий]] [[чотирикутник]], усі сторони якого є дотичними до [[Коло|кола]], розташованого всередині чотирикутника. Також має назву '''дотичний чотирикутник''' ([[Англійська мова|англ.]] tangential quadrilateral). <ref name="Josefsson Martin">{{citation |
||
|last1=Josefsson|first1=Martin |
|||
|journal=Forum Geometricorum |
|||
|title= When is a Tangential Quadrilateral a Kite? |
|||
|url=https://forumgeom.fau.edu/FG2011volume11/FG201117.pdf |
|||
|volume=11 |
|||
|year=2011 |
|||
|pages=165–174 |
|||
|issn= 1534-1178 |
|||
}}</ref>{{rp|cтор.65}} |
|||
Це коло називається [[Вписане коло|вписаним колом]] чотирикутника, а його центр ''<big>I</big>'' — ''інцентром''. |
|||
Центр вписаного в чотирикутник кола лежить на перетині [[Бісектриса|бісектрис]] чотирьох його внутрішніх кутів. |
|||
Описаний чотирикутник є окремим випадком [[Описаний багатокутник|описаного багатокутника]]. |
Описаний чотирикутник є окремим випадком [[Описаний багатокутник|описаного багатокутника]]. |
||
== Особливі випадки == |
|||
==Критерій== |
|||
Не кожен чотирикутник можна описати навколо кола. Прикладом чотирикутника, який не можна описати навколо кола, є [[прямокутник]], який не є квадратом. |
|||
В чотирикутник можна вписати коло тоді й тільки тоді, коли суми його протилежних сторін рівні. |
|||
Будь-який [[дельтоїд]] (в тому числі і [[ромб]], [[квадрат]]) можна описати навколо кола. {{Sfn|Істер О.С.|2021}}{{rp|cтор.55}} Дельтоїди також є [[Зовні-описаний чотирикутник|зовні-описаними чотирикутниками]], та чотирикутниками з перпендикулярними діагоналями ([[Ортодіагональний чотирикутник|ортодіагональними]]).<ref name="Josefsson">{{citation |
|||
|last=Josefsson|first=Martin |
|||
|journal=Forum Geometricorum|pages=119–130 |
|||
|title=Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral |
|||
|url=http://forumgeom.fau.edu/FG2010volume10/FG201013.pdf |
|||
|volume=10|year=2010}}.</ref> |
|||
В [[Трапеція|трапецію]] можна вписати коло, якщо сума довжин її основ рівна сумі довжин її бокових сторін. |
|||
[[Біцентричний чотирикутник]] — це [[вписаний чотирикутник]], який також є [[Описаний чотирикутник|описаним]]. Прикладом може бути [[прямокутний дельтоїд]], або [[рівнобічна трапеція]], у якої висота є [[Середнє геометричне|середнім геометричним]] між її основами. |
|||
== Умови, за яких чотирикутник є описаним == |
|||
У цьому розділі наведено [[Необхідна і достатня умова|необхідні та достатні умови]], щоб чотирикутник був описаним. |
|||
* Опуклий чотирикутник можна описати [[тоді й лише тоді]], коли чотири бісектриси його внутрішніх кутів є [[Конкурентні прямі|конкурентними]], тобто, перетинаються в одній точці.<ref name=Andreescu>{{citation |
|||
|last1=Andreescu|first1=Titu|last2=Enescu|first2=Bogdan |
|||
|title=Mathematical Olympiad Treasures |
|||
|url=https://artofmaths.files.wordpress.com/2014/06/mathematical-olympiad-treasures-2ed-springer-2011.pdf |
|||
|publisher=Birkhäuser |
|||
|year=2006 |
|||
|pages=253: 62–65 |
|||
|isbn=978-0-8176-8252-1 |
|||
|doi=10.1007/978-0-8176-8253-8}}.</ref>{{rp|cтор.62}} |
|||
Ця спільна точка є центром [[Описане коло|вписаного кола]]. Також в цій точці перетинаються бісектриси внутрішніх кутів, утворених при перетині прямих, що містять протилежні сторони чотирикутника. |
|||
* '''Сума протилежних сторін.''' |
|||
Згідно з [[Теорема Піто|'''теоремою Піто''']]: {{Sfn|Істер О.С.|2021}}{{rp|cтор.55 ;}} <ref name="Andreescu" />{{rp|cтор.62-64 ;}} <ref name="Durell">{{citation|first1=C. V.|last1=Durell|first2=A.|last2=Robson|title=Advanced Trigonometry|url=https://web.archive.org/web/20210922025823/https://books.google.com/books?id=3iYbExAsepEC|year=2003|publisher=Courier Dover|isbn=978-0-486-43229-8|origyear=1930|archive-date=22 вересня 2021|archive-url=https://vdocuments.mx/1930-advanced-trigonometry-durell-robsonpdf.html?page=21}}</ref>{{rp|стор.27-28 ;}} <ref name="Josefson1">{{citation|first=Martin|last=Josefsson|url=http://forumgeom.fau.edu/FG2011volume11/FG201108.pdf|title=More characterizations of tangential quadrilaterals|journal=Forum Geometricorum|volume=11|year=2011|pages=65–82|mr=2877281}}</ref> |
|||
Опуклий чотирикутник {{math|''ABCD''}} з послідовними сторонами a, b, c, d можна описати навколо [[Коло|кола]] [[Тоді й лише тоді|тоді і лише тоді]], коли суми його протилежних сторін рівні. |
|||
:<math>a+c=b+d</math> |
|||
: Те, що це твердження є також і [[Необхідна і достатня умова|достатньою умовою]], було доведено [[Якоб Штейнер|Якобом Штейнером]] у 1846 році.<ref name="Josefson1" /> |
|||
Має місце і зворотня теорема, яка запропонована також Я.Штейнером {{Sfn|Мерзляк А.Г., Полонський В.Б.|2021}}{{rp|cтор.64. теорема 10.4}} : |
|||
: ''Якщо суми протилежних сторін чотирикутника рівні, то цей чотирикутник є описаним навколо деякого кола.''[[Файл:Описаний чотирикутник 1.png|міні|Перетин протилежних сторін описаного чотирикутника|402x402пкс]] |
|||
* Якщо протилежні сторони опуклого чотирикутника ''ABCD,'' який не є ''[[Трапеція|трапецією]],'' перетинаються в точках ''E'' та ''F'' (прямі АВ і CD перетинаються в E, а прямі AD і BC перетинаються в F), то чотирикутник є описаним [[Тоді й лише тоді|тоді і лише тоді]], коли: <ref name="Andreescu" />{{rp|cтор.64-65 ;}} |
|||
:<math>\displaystyle BE+BF=DE+DF</math> |
|||
або |
|||
:<math>\displaystyle AF-AE=CF-CE</math> |
|||
[[Файл:Описаний чотирикутник 2, вписані кола в трикутники, утворені діагоналями.png|ліворуч|міні|347x347пкс|Вписані кола в трикутники, утворені при перетині діагоналей]] |
|||
* Ще одна [[необхідна і достатня умова]] полягає в тому, що опуклий чотирикутник ABCD є описаним [[Тоді й лише тоді|тоді і тільки тоді]], коли кола, вписані в два трикутники ABC і ADC (або ABD i BCD), дотичні одне до одного. <ref name="Josefson1" /> {{rp|cтор.66-67 ;}} |
|||
* Діагоналі опуклого чотирикутника ABCD при перетині ділять його на чотири трикутники ''∆ABD'', ''∆ABC'' , ''∆BCD'', ''∆ACD.'' Кола, вписані кола в ці трикутники, дотикаються до сторін чотирикутника у восьми точках, по дві на кожну сторону. Чотирикутник є описаним чотирикутником тоді і тільки тоді, коли суми відстаней між точками дотику на протилежних сторонах чотирикутника рівні:<ref name="Josefson1" /> {{rp|cтор.68}} |
|||
<math>\displaystyle KL+MN=TR+VW</math> |
|||
* У 1954 році Маріус Йосіфеску (Marius Iosifescu) довів, що опуклий чотирикутник має вписане коло [[Тоді й лише тоді|тоді і тільки тоді]], коли<ref name="Minculete"> |
|||
{{citation |
|||
|last=Minculete |first=Nicusor |
|||
|journal=Forum Geometricorum |
|||
|pages=113–118 |
|||
|title=Characterizations of a Tangential Quadrilateral |
|||
|url=http://forumgeom.fau.edu/FG2009volume9/FG200910.pdf |
|||
|volume=9 |
|||
|year=2009}}.</ref><br /><math>\tan{\frac{\angle ABD}{2}}\cdot\tan{\frac{\angle BDC}{2}}=\tan{\frac{\angle ADB}{2}}\cdot\tan{\frac{\angle DBC}{2}}.</math> |
|||
[[Файл:Tangential-quad-external-circles.svg|міні|281x281пкс|Вписані ззовні кола опуклого чотирикутника ABCD ]] |
|||
* Крім того, опуклий чотирикутник з послідовними сторонами a, b, c, d є описаним [[Тоді й лише тоді|тоді і тільки тоді]], коли: |
|||
<math>R_aR_c=R_bR_d</math> |
|||
де ''R''<sub>''a''</sub>, ''R''<sub>''b''</sub>, ''R''<sub>''c''</sub>, ''R''<sub>''d''</sub> — радіуси вписаних ззовні кіл чотирикутника ABCD, які зовнішньо дотикаються до сторін a, b, c, d відповідно, і продовжень двох суміжних сторін для кожної сторони.<ref>{{citation|last=Josefsson|first=Martin|journal=Forum Geometricorum|pages=63–77|title=Similar Metric Characterizations of Tangential and Extangential Quadrilaterals|url=http://forumgeom.fau.edu/FG2012volume12/FG201207.pdf|volume=12|year=2012}}</ref>{{rp|стор.72}} |
|||
== Властивості == |
|||
[[File:Tangentenviereck.png|286x286px|thumb|Tangential quadrilateral with inradius ''r'']] |
|||
Всі сторони описаного чотирикутника є [[Дотична пряма до кола|дотичними]] до кола |
|||
[[Перпендикулярність|Перпендикуляр]], опущений з центра вписаного кола на будь-яку сторону описаного чотирикутника дорівнює радіусу кола. |
|||
Чотири відрізки між центром вписаного кола та точками дотику до чотирикутника розділяють чотирикутник на чотири [[Прямокутний дельтоїд|прямокутних дельтоїда]] . |
|||
Якщо пряма розділяє описаний чотирикутник на два [[Многокутник|багатокутники]] з рівними [[Площа|площами]] та рівними [[Периметр|периметрами]], то ця пряма проходить через центр вписаного кола.<ref name="Andreescu" /> |
|||
== Формули для описаного чотирикутника == |
|||
=== Площа === |
|||
==== Нетригонометричні формули ==== |
|||
* [[Площа|Площу]] описаного чотирикутника ABCD зі сторонами a, b, c, d можна знайти за формулою: |
|||
<math>S = r \cdot p,</math> |
|||
де ''<big>r</big> —'' радіус вписаного кола'','' <math>p = \frac{a + b + c + d}{2}</math> ''—'' [[півпериметр]] чотирикутника ABCD. |
|||
Ця формула площі справедлива для всіх описаних багатокутників. |
|||
* Формула площі описаного чотирикутника ''ABCD'' через його сторони та діагоналі: <ref name="Durell" />{{rp|стор.29 ;}} |
|||
<math>S = \tfrac{1}{2}\sqrt{p^2q^2-(ac-bd)^2}</math> |
|||
* Формула площі описаного чотирикутника ''ABCD'' через довжини дотичних [[Відрізок|відрізків]] ''e'', ''f'', ''g'', ''h: <ref name="Josefsson" />{{rp|стор.119 ;}}'' |
|||
<math>S=\sqrt{(e+f+g+h)(efg+fgh+ghe+hef)}.</math> |
|||
* А також: ''<ref name="Josefsson" />{{rp|стор.128 ;}}'' |
|||
<math>S=\sqrt{abcd-(eg-fh)^2}.</math> |
|||
Оскільки <math>e\cdot g=f \cdot h</math> [[Тоді й лише тоді|тоді і тільки тоді]], коли описаний чотирикутник ''ABCD'' також є [[Вписаний чотирикутник|вписаним]], тобто ''ABCD —'' [[Біцентричний чотирикутник|біцентричний]] <ref name="Hajja">{{citation |
|||
|last=Hajja |first=Mowaffaq |
|||
|journal=Forum Geometricorum |
|||
|pages=103–106 |
|||
|title=A condition for a circumscriptible quadrilateral to be cyclic |
|||
|url=http://forumgeom.fau.edu/FG2008volume8/FG200814.pdf |
|||
|volume=8 |
|||
|year=2008}}</ref>{{rp|стор.104 ;}} , то з формули видно, що описаний чотирикутник має [[Екстремум|максимальну]] площу <math>S=\sqrt{abcd}.</math> тоді і тільки тоді, коли він є біцентричним. |
|||
==== Тригонометричні формули ==== |
|||
* Формула площі описаного чотирикутника ''ABCD'' через його сторони ''a'', ''b'', ''c'', ''d'' та два протилежних кута: <ref name="Durell" />''{{rp|стор.28 ;}}'' <ref>{{citation |
|||
|last1=Siddons|first1=A.W.|last2=Hughes|first2=R.T. |
|||
|title=Trigonometry |
|||
|publisher=Cambridge Univ. Press |
|||
|year=1929 |
|||
|page=203}}.</ref> <ref name="Grinberg">{{citation |
|||
|last=Grinberg |first=Darij |
|||
|title=Circumscribed quadrilaterals revisited |
|||
|url=http://www.cip.ifi.lmu.de/~grinberg/CircumRev.pdf |
|||
|pages=1-46 |
|||
|year=2021}}</ref>{{rp|стор.24, теорема12 ;}} <ref name="Yiu">{{citation |
|||
|last=Yiu |first=Paul |
|||
|title=''Euclidean Geometry'' |
|||
|url=http://math.fau.edu/Yiu/EuclideanGeometryNotes.pdf |
|||
|pages=170: 156–157 |
|||
|year=1998}}</ref>{{rp|стор.156–157 ;}} |
|||
:<math>S = \sqrt{abcd} \cdot \sin \frac{A+C}{2} = \sqrt{abcd} \cdot \sin \frac{B+D}{2}.</math> |
|||
Для заданих довжин сторін площа є максимальною, коли чотирикутник також є [[Вписаний чотирикутник|вписаним]] і, отже, [[Біцентричний чотирикутник|біцентричним чотирикутником]]. Для нього: <math>\sin \frac{A+C}{2} = |
|||
\sin \frac{B+D}{2}= \sin 90^\circ= 1</math>, а отже, <math>S = \sqrt{abcd}</math> |
|||
* Формула площі описаного чотирикутника ''ABCD'' через дві сусідні сторони та два протилежних кута: <ref name="Durell" />{{rp| стор.30}} |
|||
<math>S=ab\sin{\frac{B}{2}}\csc{\frac{D}{2}}\sin \frac{B+D}{2}.</math> |
|||
* Формула площі описаного чотирикутника ''ABCD'' через сторони ''a'', ''b'', ''c'', ''d'' та кут між діагоналями: <ref name="Durell" />{{rp| стор.29}} |
|||
<math>S=\tfrac{1}{2}|(ac-bd)\tan{\theta}|</math> |
|||
Цю формулу не можна використовувати для [[Дельтоїд|дельтоїдів]], оскільки в них діагоналі [[Перпендикулярність|перпендикулярні]]: θ = 90°, і функція [[Тригонометричні функції|тангенса]] не визначена. |
|||
* Формула площі описаного чотирикутника ''ABCD'' через відстані від його вершин до центра вписаного кола ''<big>I</big>'' та два протилежних кута:<ref name="Grinberg" />{{rp|стор.19}} |
|||
<math>S=\left(IA\cdot IC+IB\cdot ID\right)\sin\frac{A+C}{2}</math> |
|||
===Нерівності, пов'язані з площею=== |
|||
Як опосередковано зазначено вище, [[площа]] описаного чотирикутника зі сторонами ''a'', ''b'', ''c'', ''d'' задовольняє [[Нерівність|нерівності]]: |
|||
<math>S\le\sqrt{abcd}</math> |
|||
Рівність досягається тільки для [[Біцентричний чотирикутник|біцентричного чотирикутника]]. |
|||
За Т. А. Івановою (1976 р.), [[півпериметр]] p описаного чотирикутника задовольняє нерівності: |
|||
<math>p\ge 4r</math> |
|||
де ''<big>r</big>'' - радіус вписаного кола. Рівність досягається [[Тоді й лише тоді|тоді і тільки тоді]], коли чотирикутник є [[Квадрат|квадратом]]. |
|||
Це означає, що для площі ''K'' = ''r p'' існує нерівність |
|||
<math>S\ge 4r^2</math> |
|||
де рівність досягається тоді і тільки тоді, коли описаний чотирикутник є квадратом. |
|||
As indirectly noted above, the area of a tangential quadrilateral with sides ''a'', ''b'', ''c'', ''d'' satisfies |
|||
=== Радіус вписаного кола === |
|||
Радіус вписаного кола описаного чотирикутника ABCD зі сторонами ''a'', ''b'', ''c'', ''d'' та площею ''S'', можна обчислити за формулою: <ref name="Durell" /> {{rp|стор.28}} |
|||
:<math>r=\frac{S}{p}=\frac{S}{a+c}=\frac{S}{b+d}</math> |
|||
Описаний чотирикутник з даними сторонами має [[Екстремум|максимальний]] радіус вписаного кола, якщо чотирикутник є одночасно і [[Вписаний чотирикутник|вписаним]] (тобто біцентричним). |
|||
Радіус вписаного кола описаного чотирикутника ''ABCD'' через довжини дотичних [[Відрізок|відрізків]] ''e'', ''f'', ''g'', ''h: <ref name="Hajja" />{{rp|стор.104, Лемма2 ;}} <ref>{{citation|last=Hoyt|first=John P.|journal={{Не перекладено|Mathematics Magazine|Mathematics Magazine|en|Mathematics Magazine}}|pages=239, 242|title=Quickies, Q694|volume=57|number=4|year=1984}}.</ref>'' |
|||
:<math>\displaystyle r=\sqrt{\frac{efg+fgh+ghe+hef}{e+f+g+h}}.</math> |
|||
==Часткові випадки== |
==Часткові випадки== |
||
| Рядок 15: | Рядок 219: | ||
==Див. також== |
==Див. також== |
||
*[[Вписаний чотирикутник]] |
*[[Вписаний чотирикутник]] |
||
== Примітки == |
|||
{{reflist|2}} |
|||
== Література == |
|||
* {{Книга |
|||
|автор = Істер О.С. |
|||
|заголовок = |
|||
|рік = 2021 |
|||
|том = |
|||
|сторінки = 240 |
|||
|назва = Геометрія: 8 клас |
|||
|url=https://pidruchnyk.com.ua/804-geometriya-8-klas-ister-2016.html |
|||
|видавництво = Генеза |
|||
|місце = Київ |
|||
|ISBN = 978-966-11-1191-1 |
|||
|посилання = https://pidruchnyk.com.ua/804-geometriya-8-klas-ister-2016.html |
|||
|ref = Істер О.С. |
|||
}} |
|||
* {{Книга |
|||
|автор = Мерзляк А.Г., Полонський В.Б., Якір М.С. |
|||
|ref = Мерзляк А.Г., Полонський В.Б. |
|||
|назва = Геометрія: підруч. для 8 кл. загальноосвіт. навч. закладів |
|||
|посилання = https://pidruchnyk.com.ua/796-merzlyak-2016-geometriya-8-klas.html |
|||
|рік = 2021 |
|||
|сторінки = 208 : стор. 64-65 |
|||
|видання = 2-ге. переробл. |
|||
|видавництво = Гімназія |
|||
|місце = Харків |
|||
|ISBN = 978-966-474-275-4 |
|||
}} |
|||
{{geometry-stub}} |
{{geometry-stub}} |
||
Версія за 19:13, 6 серпня 2023
| Ця стаття не містить посилань на джерела. (травень 2018) |
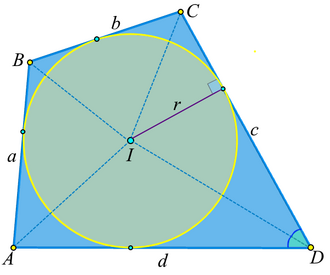
В Евклідовій геометрії описаний чотирикутник [1] — опуклий чотирикутник, усі сторони якого є дотичними до кола, розташованого всередині чотирикутника. Також має назву дотичний чотирикутник (англ. tangential quadrilateral). [2]
Це коло називається вписаним колом чотирикутника, а його центр I — інцентром.
Центр вписаного в чотирикутник кола лежить на перетині бісектрис чотирьох його внутрішніх кутів.
Описаний чотирикутник є окремим випадком описаного багатокутника.
Особливі випадки
Не кожен чотирикутник можна описати навколо кола. Прикладом чотирикутника, який не можна описати навколо кола, є прямокутник, який не є квадратом.
Будь-який дельтоїд (в тому числі і ромб, квадрат) можна описати навколо кола. [1] Дельтоїди також є зовні-описаними чотирикутниками, та чотирикутниками з перпендикулярними діагоналями (ортодіагональними).[3]
В трапецію можна вписати коло, якщо сума довжин її основ рівна сумі довжин її бокових сторін.
Біцентричний чотирикутник — це вписаний чотирикутник, який також є описаним. Прикладом може бути прямокутний дельтоїд, або рівнобічна трапеція, у якої висота є середнім геометричним між її основами.
Умови, за яких чотирикутник є описаним
У цьому розділі наведено необхідні та достатні умови, щоб чотирикутник був описаним.
- Опуклий чотирикутник можна описати тоді й лише тоді, коли чотири бісектриси його внутрішніх кутів є конкурентними, тобто, перетинаються в одній точці.[4]
Ця спільна точка є центром вписаного кола. Також в цій точці перетинаються бісектриси внутрішніх кутів, утворених при перетині прямих, що містять протилежні сторони чотирикутника.
- Сума протилежних сторін.
Згідно з теоремою Піто: [1] [4] [5] [6]
Опуклий чотирикутник ABCD з послідовними сторонами a, b, c, d можна описати навколо кола тоді і лише тоді, коли суми його протилежних сторін рівні.
- Те, що це твердження є також і достатньою умовою, було доведено Якобом Штейнером у 1846 році.[6]
Має місце і зворотня теорема, яка запропонована також Я.Штейнером [7] :
- Якщо суми протилежних сторін чотирикутника рівні, то цей чотирикутник є описаним навколо деякого кола.

Перетин протилежних сторін описаного чотирикутника
- Якщо протилежні сторони опуклого чотирикутника ABCD, який не є трапецією, перетинаються в точках E та F (прямі АВ і CD перетинаються в E, а прямі AD і BC перетинаються в F), то чотирикутник є описаним тоді і лише тоді, коли: [4]
або

- Ще одна необхідна і достатня умова полягає в тому, що опуклий чотирикутник ABCD є описаним тоді і тільки тоді, коли кола, вписані в два трикутники ABC і ADC (або ABD i BCD), дотичні одне до одного. [6]
- Діагоналі опуклого чотирикутника ABCD при перетині ділять його на чотири трикутники ∆ABD, ∆ABC , ∆BCD, ∆ACD. Кола, вписані кола в ці трикутники, дотикаються до сторін чотирикутника у восьми точках, по дві на кожну сторону. Чотирикутник є описаним чотирикутником тоді і тільки тоді, коли суми відстаней між точками дотику на протилежних сторонах чотирикутника рівні:[6]
- У 1954 році Маріус Йосіфеску (Marius Iosifescu) довів, що опуклий чотирикутник має вписане коло тоді і тільки тоді, коли[8]

- Крім того, опуклий чотирикутник з послідовними сторонами a, b, c, d є описаним тоді і тільки тоді, коли:
де Ra, Rb, Rc, Rd — радіуси вписаних ззовні кіл чотирикутника ABCD, які зовнішньо дотикаються до сторін a, b, c, d відповідно, і продовжень двох суміжних сторін для кожної сторони.[9]
Властивості

Всі сторони описаного чотирикутника є дотичними до кола
Перпендикуляр, опущений з центра вписаного кола на будь-яку сторону описаного чотирикутника дорівнює радіусу кола.
Чотири відрізки між центром вписаного кола та точками дотику до чотирикутника розділяють чотирикутник на чотири прямокутних дельтоїда .
Якщо пряма розділяє описаний чотирикутник на два багатокутники з рівними площами та рівними периметрами, то ця пряма проходить через центр вписаного кола.[4]
Формули для описаного чотирикутника
Площа
Нетригонометричні формули
- Площу описаного чотирикутника ABCD зі сторонами a, b, c, d можна знайти за формулою:
де r — радіус вписаного кола, — півпериметр чотирикутника ABCD.
Ця формула площі справедлива для всіх описаних багатокутників.
- Формула площі описаного чотирикутника ABCD через його сторони та діагоналі: [5]
- А також: [3]
Оскільки тоді і тільки тоді, коли описаний чотирикутник ABCD також є вписаним, тобто ABCD — біцентричний [10] , то з формули видно, що описаний чотирикутник має максимальну площу тоді і тільки тоді, коли він є біцентричним.
Тригонометричні формули
- Формула площі описаного чотирикутника ABCD через його сторони a, b, c, d та два протилежних кута: [5] [11] [12] [13]
Для заданих довжин сторін площа є максимальною, коли чотирикутник також є вписаним і, отже, біцентричним чотирикутником. Для нього: , а отже,
- Формула площі описаного чотирикутника ABCD через дві сусідні сторони та два протилежних кута: [5]
- Формула площі описаного чотирикутника ABCD через сторони a, b, c, d та кут між діагоналями: [5]
Цю формулу не можна використовувати для дельтоїдів, оскільки в них діагоналі перпендикулярні: θ = 90°, і функція тангенса не визначена.
- Формула площі описаного чотирикутника ABCD через відстані від його вершин до центра вписаного кола I та два протилежних кута:[12]
Нерівності, пов'язані з площею
Як опосередковано зазначено вище, площа описаного чотирикутника зі сторонами a, b, c, d задовольняє нерівності:
Рівність досягається тільки для біцентричного чотирикутника.
За Т. А. Івановою (1976 р.), півпериметр p описаного чотирикутника задовольняє нерівності:
де r - радіус вписаного кола. Рівність досягається тоді і тільки тоді, коли чотирикутник є квадратом.
Це означає, що для площі K = r p існує нерівність
де рівність досягається тоді і тільки тоді, коли описаний чотирикутник є квадратом.
As indirectly noted above, the area of a tangential quadrilateral with sides a, b, c, d satisfies
Радіус вписаного кола
Радіус вписаного кола описаного чотирикутника ABCD зі сторонами a, b, c, d та площею S, можна обчислити за формулою: [5]
Описаний чотирикутник з даними сторонами має максимальний радіус вписаного кола, якщо чотирикутник є одночасно і вписаним (тобто біцентричним).
Радіус вписаного кола описаного чотирикутника ABCD через довжини дотичних відрізків e, f, g, h: [10] [14]
Часткові випадки
Див. також
Примітки
- ↑ а б в Істер О.С., 2021.
- ↑ Josefsson, Martin (2011), When is a Tangential Quadrilateral a Kite? (PDF), Forum Geometricorum, 11: 165—174, ISSN 1534-1178
- ↑ а б в Josefsson, Martin (2010), Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral (PDF), Forum Geometricorum, 10: 119—130.
- ↑ а б в г Andreescu, Titu; Enescu, Bogdan (2006), Mathematical Olympiad Treasures (PDF), Birkhäuser, с. 253: 62–65, doi:10.1007/978-0-8176-8253-8, ISBN 978-0-8176-8252-1.
- ↑ а б в г д е Durell, C. V.; Robson, A. (2003) [1930], Advanced Trigonometry, Courier Dover, ISBN 978-0-486-43229-8, архів оригіналу за 22 вересня 2021
- ↑ а б в г Josefsson, Martin (2011), More characterizations of tangential quadrilaterals (PDF), Forum Geometricorum, 11: 65—82, MR 2877281
- ↑ Мерзляк А.Г., Полонський В.Б., 2021.
- ↑ Minculete, Nicusor (2009), Characterizations of a Tangential Quadrilateral (PDF), Forum Geometricorum, 9: 113—118.
- ↑ Josefsson, Martin (2012), Similar Metric Characterizations of Tangential and Extangential Quadrilaterals (PDF), Forum Geometricorum, 12: 63—77
- ↑ а б Hajja, Mowaffaq (2008), A condition for a circumscriptible quadrilateral to be cyclic (PDF), Forum Geometricorum, 8: 103—106
- ↑ Siddons, A.W.; Hughes, R.T. (1929), Trigonometry, Cambridge Univ. Press, с. 203.
- ↑ а б Grinberg, Darij (2021), Circumscribed quadrilaterals revisited (PDF), с. 1—46
- ↑ Yiu, Paul (1998), Euclidean Geometry (PDF), с. 170: 156–157
- ↑ Hoyt, John P. (1984), Quickies, Q694, Mathematics Magazine[en], 57 (4): 239, 242.
Література
- Істер О.С. Геометрія: 8 клас. — Київ : Генеза, 2021. — С. 240. — ISBN 978-966-11-1191-1.
- Мерзляк А.Г., Полонський В.Б., Якір М.С. Геометрія: підруч. для 8 кл. загальноосвіт. навч. закладів. — 2-ге. переробл. — Харків : Гімназія, 2021. — С. 208 : стор. 64-65. — ISBN 978-966-474-275-4.
| Це незавершена стаття з геометрії. Ви можете допомогти проєкту, виправивши або дописавши її. |
























