Парадокс Бертрана (теорія ймовірностей)

Парадокс Бертрана це задача в класичному означенні ймовірності. Джозеф Бертран вперше описав її в своїй праці Calcul des probabilités (1888) як приклад того, що ймовірність не може бути чітко означена, поки чітко не описаний механізм отримання випадковостей.

Для деякого кола випадковим чином обирається хорда. Знайти ймовірність того, що ця хорда довша за сторони правильного трикутника, вписаного в це коло. (Варіанти — довша за радіус, або знайти матсподівання її довжини). Парадокс стверджує, що ця ймовірність визначається неоднозначно залежно від методу.

• 
  Метод перший
• 
  Метод другий
• 
  Третій метод

Метод перший

Випадковим шляхом (рівномірно) в даному крузі обирається точка. Ця випадкова точка визначає єдину хорду, серединою якої вона є. Ця хорда довша за сторони нашого вписаного правильного трикутника тоді і тільки тоді, коли її середина лежить всередині кола, вписаного в трикутник. Радіус цього кола дорівнює половині радіуса вихідного кола, отже площа його становить 1/4 площі вихідного. Таким чином, ймовірність того, що випадково обрана точка лежить всередині вписаного кола, дорівнює 1/4. Отже, цей метод дає відповідь ¼.

Метод другий

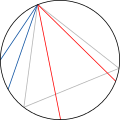
Виходячи з міркувань симетрії, можна вважати, що одним кінцем хорди є фіксована точка на колі. Нехай цією точкою є вершина вписаного трикутника. Оберемо другий кінець випадково з рівномірним розподілом. Вершини трикутника ділять коло на три рівні дуги, і випадкова хорда довша за сторони правильного трикутника, якщо вона перетинає цей трикутник. Отже, шукана ймовірність тепер дорівнює ⅓.

Третій метод

Оберемо точку випадковим чином рівномірно на радіусі кола і візьмемо хорду, яка перпендикулярна цьому радіусу і проходить через обрану точку. Тоді випадкова хорда довша за сторони вписаного правильного трикутника, якщо випадкова точка лежить на тій половині радіусу, яка ближча до центра. Виходячи з міркувань симетрії, неважливо, який радіус був обраний для побудови, тому шукана ймовірність дорівнює ½.

Джерела

• Г. Секей. «Парадоксы в теории вероятностей и математической статистике» М., Мир 1990.(рос.)