Парадокс днів народження
У теорії ймовірностей парадокс днів народження[1] оцінює ймовірність того, що у випадково вибраній групі людей збігатимуться дні народження в якоїсь пари. В групах кількістю не менших 23 випадково вибраних людей, ймовірність збігу днів народження в якоїсь пари становить більше 50 %. Такий результат суперечить інтуїтивній уяві більшості.
Для 57 людей, ймовірність становить більше ніж 99 %, і досягає 100 % коли, ігноруючи високосний рік, кількість людей у групі становить 366 (через принцип Діріхле). Такий розподіл ймовірностей призвів до широко відомої криптографічної атаки відомої як атака «днів народження».

У формулюванні парадоксу йдеться саме про збіг днів народження у будь-яких двох членів групи. Одна з поширених помилок полягає в тому, що цей випадок плутають з іншим випадком, на перший погляд схожим, коли з групи вибирається одна людина, й оцінюється ймовірність того, що день народження будь-яких інших членів групи збіжиться з днем народження вибраної людини. В останньому випадку ймовірність збігу значно нижча.
Розуміння проблеми[ред. | ред. код]
В парадоксі днів народження з'ясовується, чи хтось з випадково вибраних 23 людей буде мати день народження в один день з кимось іншим з групи.
У списку з 23 людей, при порівнянні днів народження з першою в списку людиною, існує 22 шанси на збіг, але порівняння кожного з кожним дає 253 різні шанси: в групі з 23 людей, утворюється пари. Припускаємо, що всі дні народження однаково ймовірні[2], ймовірність мати день народження в певний день для конкретної людини становить (нехтуємо високосний рік, 29 лютого). Поглянувши на число можливих пар, вже значно легше прийняти факт того, що ймовірність збігу днів народження становить понад 50 %, хоча й неправильно казати, що розподіл за парами групи з 23 людей еквівалентний 253 парам вибраним незалежно.
Обчислення ймовірності[ред. | ред. код]
Задача полягає в обчисленні приблизної ймовірності того, що в кімнаті з людьми, щонайменше двоє мають один і той самий день народження. Для спрощення не зважатимемо на нерівномірність розподілу народжуваності протягом року, і припустимо, що існує 365 днів рівних між собою. У справжньому житті розподіл днів народження неоднаковий.
Якщо ймовірність збігу щонайменше двох днів народження, тоді можливо буде легше обчислити , ймовірність того, що в групі немає двох людей з однаковим днем народження. Через те, що та — єдині дві можливі ймовірності і вони виключають одна одну, .
Коли події незалежні одна від одної, ймовірність настання їх усіх дорівнює добутку ймовірностей кожної окремої події. Через це, якщо можна описати як 23 незалежні події, тоді може бути вирахувана як .
23 людей відповідають 23 незалежним подіям, які можна розташувати за порядком. Кожна подія може бути визначена як те, що відповідна людина має різні дні народження з усіма попередньо відібраними людьми. Для події 1 попередньо відібраних людей не має. Таким чином ймовірність того, що людина 1 не має однакових днів народження з попередньо відібраними людьми становить 100 %. Враховуючи, що ми нехтуємо високосний рік, ймовірність 1 може бути записана як , з причин які стануть зрозумілими далі. Для події 2, попередньо відібрана людина тільки одна. В нашому припущенні того, що день народження може з однаковою ймовірністю статися в будь-який день року, ймовірність , що людина 2 має відмінний від людини 1 день народження, становить . Це правильно з огляду на те, що людина 2 може народитися в будь-який з 364 серед 365 днів року і при цьому мати різні дні народження з людиною 1.
Так само, людина 3 може народитися в будь-який з 363 днів року, відмінних від днів народження перших двох, і ймовірність .
Цей розбір продовжується до досягнення 23-ї людини, і .
P(A') дорівнює добутку окремих ймовірностей:
-
()
Рівняння (1) можна далі записати як:
-
()
Для подальшого спрощення рівняння (2), розпишемо факторіал 365 як:
І поділимо обидві частини на :
-
()
Тепер підставимо рівняння (3) в рівняння (2):
-
()
Обчислення рівняння (4) нам дає .
Відповідно,
Цей процес може бути узагальнений для групи з людей, де ймовірність збігу днів народження у принаймні двох людей з . Легше спочатку вирахувати ймовірність того, що всі днів народження різні. Згідно з принципом Діріхле, коли . Коли :
Рівняння відображає описаний раніше факт отримання ймовірностей .
Ймовірність того, що принаймні двоє людей з мають однаковий день народження, комплементарна до ймовірності, що всі дні народження різні. Таким чином,

Ця ймовірність перевищує для (зі значенням біля 50.7 %). Наступна таблиця показує ймовірності для деяких інших значень (в таблиці знехтувано високосні роки):
| n | p(n) |
|---|---|
| 10 | 11.7 % |
| 20 | 41.1 % |
| 23 | 50.7 % |
| 30 | 70.6 % |
| 50 | 97.0 % |
| 57 | 99.0 % |
| 100 | 99.99997 % |
| 200 | 99.9999999999999999999999999998 % |
| 300 | (100 − (6×10−80))% |
| 350 | (100 − (3×10−129))% |
| 366 | 100 % |
Апроксимація[ред. | ред. код]
Використавши розклад експоненційної функції в ряд Тейлора

отримаємо апроксимацію першого порядку для при :
Якщо то
Перший вираз отриманий для p(n) може бути апроксимований як
Відповідно
Навіть грубіша апроксимація отримана таким чином
як показує графік, залишається досить точною.
Просте піднесення до степеня[ред. | ред. код]
Ймовірність того, що будь-які двоє людей мають різні дні народження становить 364/365. В кімнаті з n людьми, налічується C(n, 2)=n(n-1)/2 пар, тобто C(n, 2) подій. Ймовірність відсутності двох людей з однаковим днем народження може бути апроксимована припущенням того, що всі ці події незалежні і знайдена як простий добуток їх ймовірностей. Коротко кажучи, дріб 364/365 може бути помножений на себе C(n, 2) разів, що дає нам
Якщо це ймовірність, що ніхто не має однакових днів народження, тоді ймовірність наявності таких людей становить
Розподіл Пуассона[ред. | ред. код]
Якщо в кімнаті присутні людей, то маємо пар. Ми визначили успіх за наявність однієї пари з однаковим днем народження, імовірність цього . Отже
Очікувана кількість успіхів становить
Звідси, ймовірність того, що нема такої пари, є
Якщо ми бажаємо знайти кількість людей для яких імовірність менша ніж 0.5:
що дає нам , тобто якщо в кімнаті 23 людей, то ймовірність, що дні народження двох з них збігаються, дорівнює 0.5.
Розрахунок кількості осіб, за якої ймовірність становить 50 %[ред. | ред. код]
З наведеної раніше формули для p(n) виразимо n. Потім замість p(n) підставимо 50 % (0,5). В результаті отримаємо:
Існує ще один спосіб оцінення n за ймовірності 50 % Згідно доведеному вище:
Знайдемо найменше n, за якого
або, що те ж саме:
Скористаємося наведеною вище апроксимацією функції експоненційною функцією:
Підставивши замість у вираз , отримаємо:
Розв'язуючи відносно n, отримаємо:
Звідси знайдемо n і округлимо до цілого :
- n = 23.
Люди, що народились в один день із заданою людиною[ред. | ред. код]
Порівняємо ймовірність p(n) зі ймовірністю того, що в групі з n людей день народження якоїсь людини з групи збіжиться з днем народження деякої заздалегідь вибраної людини, яка не належить до групи. Ця ймовірність дорівнює

Підставляючи n = 23, маємо q(n) ≈ 6,12 %. Для того, щоб імовірність q(n) перевищила 50 %, число людей в групі має бути не меншим, ніж 253 (q(252) ≈ 49,91 %; q(253) ≈ 50,05 %). Це число більше, ніж половина днів у році (365/2 = 182,5); так виходить через те, що в решти членів групи дні народження можуть збігатися, і це зменшує ймовірність q(n).
Узагальнення[ред. | ред. код]
Збіг дискретних випадкових величин[ред. | ред. код]
Описана задача може бути сформульована в загальному вигляді:
- дані випадкові числа;
- випадкові числа розподілені рівномірно в діапазоні від 1 до d;
- n — кількість випадкових чисел;
- визначити p( n ; d ) — ймовірність того, що збіжаться хоча б два числа із заданих.
Якщо міркувати так само, як описано вище, можна отримати загальні розв'язки:
Обернена задача:
- дана p — ймовірність того, що збігаються хоча б два випадкових числа;
- відомо, що випадкові числа розподілені рівномірно в діапазоні від 1 до d;
- знайти n(p;d) — кількість випадкових чисел.
Розв'язок:
Кілька типів людей[ред. | ред. код]
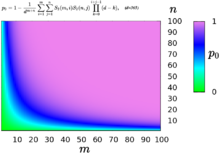
Вище парадокс днів народження був розглянутий для одного «типу» людей. Можна узагальнити задачу, ввівши кілька «типів», наприклад, розділивши людей на чоловіків (m) і жінок (n). Підрахуємо ймовірність того, що хоча б в однієї жінки і в одного чоловіка збігаються дні народження (збіг днів народження у двох жінок або у двох чоловіків не враховуються):
де d = 365 и S2() — числа Стірлінга другого роду. Цікаво, що немає однозначної відповіді на питання про величину n+m для заданої ймовірності. Наприклад, ймовірність 0,5 дає як набір з 16 чоловіків і 16 жінок, так і набір з 43 чоловіків і 6 жінок.
Близькі дні народження[ред. | ред. код]
Інше узагальнення парадоксу днів народження полягає в постановці задачі про те, скільки потрібно людей для того, щоб імовірність наявності в групі людей, дні народження яких відрізняються не більше ніж на один день (або на два, три дні і так далі), перевищила 50 %. Під час розв'язування цієї задачі використовується принцип включень-виключень. Результат (знову ж у припущенні, що дні народження розподілені рівномірно) виходить таким:
| Максимальна різниця днів народження, кількість днів | Необхідна кількість людей |
|---|---|
| 1 | 23 |
| 2 | 14 |
| 3 | 11 |
| 4 | 9 |
| 5 | 8 |
| 6 | 8 |
| 7 | 7 |
| 8 | 7 |
Таким чином, ймовірність того, що навіть у групі з 7 людей дні народження хоча б у двох з них будуть відрізнятися не більше ніж на тиждень, перевищує 50 %.
Застосування[ред. | ред. код]
Парадокс днів народження в загальному вигляді можна застосувати до хеш-функцій: якщо хеш-функція генерує N-бітове значення, то число випадкових вхідних даних, для яких хеш-коди з великою ймовірністю дадуть колізію (тобто знайдуться рівні хеш-коди, отримані на різних вхідних даних), дорівнює не 2N, а тільки близько 2N/2. Це спостереження використовується в атаці на криптографічні хеш-функції, що отримала назву «атака „днів народження“».
| N | Кількість різних вихідних ланцюжків (2N) | Імовірність хоча б однієї колізії (p) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 −18 | 10 −15 | 10 −12 | 10 −9 | 10 −6 | 0,1 % | 1 % | 25 % | 50 % | 75 % | ||
| 32 | 4,3 × 10 9 | 2 | 2 | 2 | 2.9 | 93 | 2.9 × 10³ | 9.3 × 10³ | 5.0 × 10⁴ | 7.7 × 10⁴ | 1.1 × 10⁵ |
| 64 | 1,8 × 10 19 | 6.1 | 1.9 × 10² | 6.1 × 10³ | 1.9 × 10⁵ | 6.1 × 10⁶ | 1.9 × 10⁸ | 6.1 × 10⁸ | 3.3 × 10⁹ | 5.1 × 10⁹ | 7.2 × 10⁹ |
| 128 | 3,4 × 10 38 | 2.6 × 10 10 | 8.2 × 10 11 | 2.6 × 10 13 | 8.2 × 10 14 | 2.6 × 10 16 | 8.3 × 10 17 | 2.6 × 10 18 | 1.4 × 10 19 | 2.2 × 10 19 | 3.1 × 10 19 |
| 256 | 1,2 × 10 77 | 4.8 × 10 29 | 1.5 × 10 31 | 4.8 × 10 32 | 1.5 × 10 34 | 4.8 × 10 35 | 1.5 × 10 37 | 4.8 × 10 37 | 2.6 × 10 38 | 4.0 × 10 38 | 5.7 × 10 38 |
| 384 | 3,9 × 10 115 | 8.9 × 10 48 | 2.8 × 10 50 | 8.9 × 10 51 | 2.8 × 10 53 | 8.9 × 10 54 | 2.8 × 10 56 | 8.9 × 10 56 | 4.8 × 10 57 | 7.4 × 10 57 | 1.0 × 10 58 |
| 512 | 1,3 × 10 154 | 1.6 × 10 68 | 5.2 × 10 69 | 1.6 × 10 71 | 5.2 × 10 72 | 1.6 × 10 74 | 5.2 × 10 75 | 1.6 × 10 76 | 8.8 × 10 76 | 1.4 × 10 77 | 1.9 × 10 77 |
У білих комірках вказана кількість осіб у групі, за якої колізія відбудеться із заданою ймовірністю (за аналогією з парадоксом кількість вихідних ланцюжків становить 365).
Подібний математичний апарат використовується для оцінювання розміру популяцій риб в озерах. Метод називається «capture-recapture» («зловити-зловити знову»). Дійсно, якщо кожну спійману рибу позначати та відпускати, то ймовірність зловити позначену рибу буде зростати нелінійно (відповідно до наведеного вище графіка) зі зростанням кількості спроб. Розмір популяції грубо може бути оцінений як квадрат числа спроб, здійснених до виловлювання першої позначеної риби.
Розв'язок задачі в загальному вигляді застосовується у багатьох розділах математики, наприклад, у недетермінованих алгоритмах факторизації. Так, одне з найпростіших пояснень ρ-методу Полларда аналогічне поясненню парадоксу днів народження: досить мати приблизно випадкових чисел від 0 до , де — прості, щоб хоча б для однієї з пар чисел з високою ймовірністю знайшовся , який і буде дільником числа n.
Обернені задачі[ред. | ред. код]
- Пошук найменшого числа n, за якого ймовірність p (n) більша від заданого числа p.
- Пошук найбільшого числа n, за якого ймовірність p(n) менша від заданого числа p.
Користуючись формулою, наведеною вище, отримуємо:
| p | n | n ↓ | p (n ↓) | n ↑ | p (n ↑) |
|---|---|---|---|---|---|
| 0.01 | 0.14178√365 = 2.70864 | 2 | 0.00274 | 3 | 0.00820 |
| 0.05 | 0.32029√365 = 6.11916 | 6 | 0.04046 | 7 | 0.05624 |
| 0.1 | 0.45904√365 = 8.77002 | 8 | 0.07434 | 9 | 0.09462 |
| 0.2 | 0.66805√365 = 12.76302 | 12 | 0.16702 | 13 | 0.19441 |
| 0.3 | 0.84460√365 = 16.13607 | 16 | 0.28360 | 17 | 0.31501 |
| 0.5 | 1.17741√365 = 22.49439 | 22 | 0.47570 | 23 | 0.50730 |
| 0.7 | 1.55176√365 = 29.64625 | 29 | 0.68097 | 30 | 0.70632 |
| 0.8 | 1.79412√365 = 34.27666 | 34 | 0.79532 | 35 | 0.81438 |
| 0.9 | 2.14597√365 = 40.99862 | 40 | 0.89123 | 41 | 0.90315 |
| 0.95 | 2.44775√365 = 46.76414 | 46 | 0.94825 | 47 | 0.95477 |
| 0.99 | 3.03485√365 = 57.98081 | 57 | 0.99012 | 58 | 0.99166 |
Найкраща позиція[ред. | ред. код]
Нехай у кімнаті знаходятся n - 1 осіб, і їхні дні народження різні. Нехай g(n) — ймовірність того, що день народження людини, яка зайшла, збігається з днем народження когось із присутніх у кімнаті. Потрібно знайти значення n, за якого значення функції g(n) максимальне.
Розв'язування зводиться до знаходження максимального значення виразу
- p(n) - p(n-1).
Використовуючи наведену вище формулу для p(n) отримаємо n = 20
Середнє число людей[ред. | ред. код]
Розглянемо іншу задачу. Скільки в середньому потрібно людей для того, щоб хоча б у двох з них збіглися дні народження?
Ця проблема мала відношення до алгоритмів хешування і була досліджена Дональдом Кнутом. Виявляється, що випадкова величина, яка нас цікавить, має математичне сподівання, рівне
де
Функція
була досліджена Рамануджаном. Він же отримав для цієї функції таке асимптотичне розкладання :
При M = 365 середня кількість людей дорівнює
Це число трохи більше, ніж число людей, що забезпечують імовірність 50 %. Як не дивно, необхідне число людей дорівнює M + 1 = 366 (у 365 людей дні народження можуть розподілитися по кожному з 365 днів року без збігів), хоча в середньому потрібно лиш 25.
Примітки[ред. | ред. код]
- ↑ Хоча це й не парадокс у сенсі отримання логічної суперечності, але він названий так через те, що математичний розв'язок суперечить наївній інтуїції: більшість людей оцінюють шанс менше ніж у 50 %.
- ↑ Насправді, дні народження нерівномірно розподілені впродовж року; але для цієї задачі вважаємо розподіл рівномірним.
Див. також[ред. | ред. код]
Посилання[ред. | ред. код]
- Парадокси теорії ймовірностей.
- Порівняльний огляд алгоритмів PGP. Парадокс «днів народження» і стійкість криптографії.
Література[ред. | ред. код]
- John G. Kemeny, J. Laurie Snell, Gerald Thompson. Introduction to Finite Mathematics. The first edition. — 1‑е издание. — 1957. (англ.)
- Кемени Дж., Снелл Дж., Томпсон Дж. Введение в конечную математику : [англ.]. — Издательство иностранной литературы, 1963. — 488 с. (рос.)
- Секей Г. Парадоксы в теории вероятностей и математической статистике. — РХД, 2003. — ISBN 5-93972-150-8. (рос.)
- Козлов М. В. Элементы теории вероятностей в примерах и задачах. — МГУ, 1990. — ISBN 5-211-00312-8. (рос.)
- Ширяев А. Н. Вероятность-1. — МЦНМО, 2007. — ISBN 978-5-94057-036-3.(рос.)
- Goldberg S. A Direct Attack on a Birthday Problem : [англ.] // Mathematical Mathematics Magazine. — травень 1976. — No. 49. — С. 130—132.(англ.)
- Mosteller F. Understanding the Birthday Problem : [англ.] // The Mathematics Teacher. — травень 1962. — С. 322—325.(англ.)
| |||||||||||||||||||
















































































