Філогенетичне дерево
| Частина серії статей на тему: |
| Еволюційна біологія |
|---|
 «Корал життя» — сучасне представлення філогенетичного древа всього живого на планеті |
|
Дисципліни і застосування
|
|
|
Філогенети́чне де́рево (еволюційне дерево, дерево життя) — дерево, що відображає еволюційні взаємозв'язки між різними видами, іншими таксонами, генами або іншими об'єктами, що мають загального предка.
Вершини філогенетичного дерева діляться на три класи: листя, вузли і (максимум один) корінь. Листя — це кінцеві вершини, тобто ті, в які входять рівно по одному ребру; кожен лист відображає деякий вид живих організмів (або інший об'єкт, схильний до еволюції, наприклад білковий домен). Кожен вузол являє еволюційну подію: розділення предкового таксона на два або більше, які надалі еволюціонували незалежно. Корінь являє собою спільного предка всіх даних об'єктів. Ребра дерева філогенезу називають «гілками».
Ідея «дерева» з'явилася в ранніх поглядах на життя, як на процес розвитку від простих форм до складних. Сучасні еволюційні біологи продовжують використовувати дерева для ілюстрації еволюції, оскільки воно наочно показує розвиток і походження видів.
Типи філогенетичних дерев[ред. | ред. код]

Вкорінене дерево — дерево, що містить виділену вершину — корінь. Вкорінене дерево можна вважати орієнтованим графом, оскільки воно має природну орієнтацію — від кореня до листя. Кожен вузол вкоріненого дерева відповідає останньому загальному предкові листя дерева, що лежить нижче. На малюнку представлене вкорінене філогенетичне дерево, забарвлене відповідно до деменам живих організмів у «системі трьох доменів»[2].
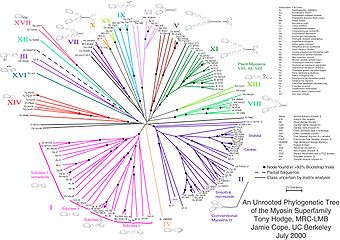
Невкорінене дерево не містить кореня і відображає зв'язок листя без передбачуваного положення загального предка. Необхідність розглядати невкорінені дерева виникає через те, що часто зв'язки між вузлами відновити легше, ніж напрямок еволюції. На другому малюнку показано невкорінене філогетичне дерево[3]. Найдостовірнішим методом для перетворення невкоріненого дерева на вкорінене (для цього треба або оголосити коренем один з вузлів, або розбити одну з гілок дві, що виходять з кореня) є використання достовірної «зовнішньої групи» видів — достатньо близьких до набору видів, що цікавлять дослідника, але в той же час вочевидь є окремою групою. В інших випадках положення кореня можна встановити, виходячи з додаткових припущень про швидкість еволюції досліджуваних об'єктів.
Як вкорінене, так і невкорінене філогенетичні дерева можуть бути біфуркаційними або мультифуркаційними, а також маркованими або немаркованими. У біфуркаційному дереві до кожного вузла підходять рівно три гілки (у разі вкоріненого дерева — одна вхідна гілка і дві вихідні). Таким чином біфуркаційне дерево припускає, що всі еволюційні події полягали в походженні від предкового об'єкта рівно двох нащадків. До вузла мультифуркаційного дерева можуть підходити чотири й більше гілок. Марковане дерево містить назви листків, тоді як немарковане просто відображає топологію.
Кількість можливих дерев для наданого ряду вершин-листів залежить від виду дерева: можливих мультифуркаційних дерев завжди більше, ніж біфуркаційних, маркованих більше, ніж немаркованих, а вкорінених — більше, ніж невкорінених. Остання відмінність має найбільше біологічне значення — існує багато місць на невкоріненому дереві, куди можна помістити корінь. Для маркованих біфуркаційних дерев існує
вкорінених дерев
невкорінених дерев, де n являє собою кількість вузлів. Кількість невкорінених дерев для n вузлів дорівнює числу вкорінених для n-1 вузлів[4].
Дендрограма — загальний термін, що позначає схематичне представлення філогенетичного дерева.
Кладограма — філогенетичне дерево, що не містить інформації про довжину гілок.
Філограма (або фенограма) — філогенетичне дерево, що містить інформацію про довжину гілок — ця довжина являє собою зміну якоїсь характеристики.
Хронограмма — філограма, довжина гілок на якій представляють еволюційний час.
Побудова філогенетичних дерев[ред. | ред. код]
Філогенетичні дерева, що складаються з нетривіального числа вхідних послідовностей будують з використанням обчислювальних методів. Дистанційні методи матрицею, таких як UPGMA, які розраховують генетичну відстань від множинного вирівнювання послідовностей, але не посилаються на еволюційну модель. Багато методів вирівнювання послідовності, такі як ClustalW також створюють дерева за допомогою простих алгоритмів (тобто ті, які засновані на відстані) в побудові дерева.
Максимальна скупість ще один простий спосіб оцінки філогенетичних дерев, але припускає неявну модель еволюції (тобто скупість).
Більш сучасні методи застосовують критерії оптимальності в максимальній ймовірності, часто в Байєсівській структурі, і застосовують явну модель еволюції до оцінки філогенетичного дерева.
Методи побудови філогенетичних дерев можуть бути оцінені на основі декількох критеріїв:[5]
- ефективність (скільки пам'яті потрібно, щоб обчислити відповідь?)
- потужність (чи дані використовуються ефективно чи даремно?)
- консистенція (чи буде сходитися на кожен раз відповідь, якщо кожен раз даються різні дані по тій же модельній задачі?)
- надійність (чи добре справляються з порушеннями припущень базової моделі?)
- фальсифікованість (якщо теорія не може бути фальсифікована, немає сенсу навіть дослідження доказів).
Методи побудови філогенетичних дерев привернули увагу математиків. Дерева можна побудувати з використанням T-теорії.[6]
Див. також[ред. | ред. код]
Примітки[ред. | ред. код]
- ↑ Hodge, T. & M. J. T. V. Cope. 2000. A Myosin Family Tree. Journal of Cell Science 113: 3353-3354. See also the Myosin external link below.
- ↑ Woese, C. R.. 1998. The Universal Ancestor. Proceedings of the National Academy of Sciences 95: 6854-6859.
- ↑ Maher, B. A. 2002. Uprooting the Tree of Life. The Scientist 16: 18 (Sep. 16, 2002); subscription only [Архівовано 2003-10-02 у Wayback Machine.]
- ↑ Felsenstein J. (2004). Inferring Phylogenies Sinauer Associates: Sunderland, MA.
- ↑ Penny, D.; Hendy, M. D.; Steel, M. A. (1992). «Progress with methods for constructing evolutionary trees». Trends in Ecology and Evolution 7: 73–79. doi:10.1016/0169-5347(92)90244-6
- ↑ A. Dress, K. T. Huber, and V. Moulton. 2001. Metric Spaces in Pure and Applied Mathematics. Documenta Mathematica LSU 2001: 121—139
Посилання[ред. | ред. код]
| Це незавершена стаття з біології. Ви можете допомогти проєкту, виправивши або дописавши її. |

