Багатогранник Дюрера

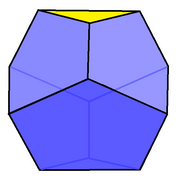
Зрізана трикутна трапеція моноліт Дюрера
Тип	Укорочена трапеція
Обличчя	6 п'ятикутників, 2 трикутники
Краї	18
Вершини	12
Група симетрії	D 3d, [2 +, 6], (2*3)
Подвійний багатогранник	Гіроелонгована трикутна біпіраміда
Властивості	опуклий

Багатогранник Дюрера — багатогранник, зображений на гравюрі Меланхолія художника Альбрехта Дюрера. У геометрії зрі́зана трикутна трапеція є однією з серії зрі́заних багатогранних трапецій. Вона має 6 п'ятикутників та 2 трикутні грані.

Геометрія

Цей багатогранник більше схожий на "якийсь момент" проходження гіперкубу з 4-го виміру через площину 3-го виміру. Якщо додати, що художник був математиком, то ймовірно він бачив цю 4-вимірну фігуру в своїй уяві в "проходженні".

Так, в 3-вимірному просторі ця фігура може бути побудована шляхом обрізання двох протилежних вершин куба, трикутного трапеції (опуклий багатогранник із шістьма сторонами ромба, утвореного розтягуванням або скороченням куба вздовж однієї з його довгих діагоналей), або з ромбоедра чи паралелепіпеда (менш симетричні багатогранники, які все ще мають таку ж комбінаторну будову, як куб). У випадку куба або тригональної трапеції, де дві зрізані вершини — це ті, що розташовуються на осях, що розтягуються, отримана форма має триразову обертальну симетрію.

Моноліт Дюрера

Меланхолія (1514 рік)

Цей багатогранник іноді називають монолітом Дюрера, через його появу в гравюрі Меланхолія 1514 року. Граф, утворений його ребрами і вершинами, називається графом Дюрера.

Форма моноліту, зображеного Дюрером, є предметом наукових дискусій, які точаться навколо того, яке геометричне тіло було зрізане: куб, чи ромбоедр.

Більшість вчених більше схиляються до другого варіанту, але існують ще декілька припущень щодо цього:

• Ріхтер стверджує, що ромби ромбоедра, з яких складається ця форма, мають 5: 6 як співвідношення між їх короткими та довгими діагоналями, від яких гострі кути ромбів становитимуть приблизно 80 °.
• Шредер (1980) та Лінч (1982) натомість роблять висновок, що відношення дорівнює √3: 2 і що кут приблизно 82 °Schröder, E. (1980), Dürer, Kunst und Geometrie, Dürers künstlerisches Schaffen aus der Sicht seiner "Underweysung", Basel Як цитує Weitzel, (2004).
• МакГілларі вимірює особливості креслення і виявляє, що кут приблизно 79 °. Він і Вольф фон Енгельгардт (див. Хідеко, 2009) стверджують, що цей вибір кута походить від його фізичного виникнення в кристалах кальциту.
• Шрайбер стверджує, що спираючись на праці Дюрера, можна стверджувати, що всі вершини моноліта Дюрера лежать на спільній сфері, а також кути ромба дорівнюють 72 °. Хідеко (2009) перераховує декількох інших науковців, які також віддають перевагу теорії 72 °, починаючи з Павла Гродзінського в 1955 році. Він стверджує, що ця теорія мотивована не лише аналізом малюнка, а насамперед естетичними принципами, що стосуються правильних п'ятикутників і золотого перетину.
• Вейцлер аналізує ескіз Дюрера 1510 р. того ж моноліта. Він підтверджує гіпотезу Шрайбера про те, що форма має окружність, але з кутами ромба приблизно 79,5 °.
• Хідеко стверджує, що форма призначена для відображення знаменитої геометричної проблеми подвоєння куба, про яку Дюрер також писав у 1525 р. Тому він робить висновок, що (перш ніж відрізати кути) форма є кубом розтягнутим по його довгій діагоналі. Більш конкретно, він стверджує, що Дюрер намалював фактичний куб з довгою діагоналлю, паралельною перспективі площини, а потім збільшив свій малюнок деяким фактором у напрямку довгої діагоналі; результат був би таким самим, як якщо б він намалював витягнуте тверде тіло. Він збільшує коефіцієнт збільшення, що має значення для подвоєння куба 2^1/3 ≈ 1.253, але Хідеко отримує інший коефіцієнт збільшення, який краще відповідає малюнку, 1.277, більш складним чином.
• Футамура, Франц і Краннел класифікують запропоновані рішення цієї проблеми за двома параметрами: гострим кутом та перехресним співвідношенням. Їх оцінка перехресного співвідношення близька до рівня МакГілларі і має числове значення, близьке до золотого перетину. Виходячи з цього, вони вважають, що гострий кут $2\arctan(\varphi /2)\approx 78^{\circ }$ і що перехресне співвідношення точно $\varphi$.

Див. також

• Скошений тетраедр, іншої форми, утворений обрізанням підмножини вершин куба

Джерела

• Lynch, Terence (1982), The geometric body in Dürer's engraving Melencolia I, Journal of the Warburg and Courtauld Institutes, The Warburg Institute, 45: 226—232, doi:10.2307/750979, JSTOR 750979
• MacGillavry, C. (1981), The polyhedron in A. Dürers Melencolia I, Nederl. Akad. Wetensch. Proc. Ser. B, 84: 287—294.
• Richter, D. H. (1957), Perspektive und Proportionen in Albrecht Dürers "Melancholie", Z. Vermessungswesen, 82: 284–288 and 350–357. Як цитує Weitzel, (2004).
• Schreiber, Peter (1999), A new hypothesis on Dürer's enigmatic polyhedron in his copper engraving "Melencolia I", Historia Mathematica, 26: 369—377, doi:10.1006/hmat.1999.2245.
• Schröder, E. (1980), Dürer, Kunst und Geometrie, Dürers künstlerisches Schaffen aus der Sicht seiner "Underweysung", Basel Як цитує Weitzel, (2004).
• Strauss, Walter L. (1972), The Complete Engravings of Dürer, New York, с. 168, ISBN 0-486-22851-7 Strauss, Walter L. (1972), The Complete Engravings of Dürer, New York, с. 168, ISBN 0-486-22851-7 . Як цитує Lynch, (1982) .
• Weber, P. (1900), Beiträge zu Dürers Weltanschauung—Eine Studie über die drei Stiche Ritter, Tod und Teufel, Melancholie und Hieronymus im Gehäus, Strassburg . Як цитує Weitzel, (2004) .
• Weitzel, Hans (2004), A further hypothesis on the polyhedron of A. Dürer's engraving Melencolia I, Historia Mathematica, 31 (1): 11—14, doi:10.1016/S0315-0860(03)00029-6 одна Weitzel, Hans (2004), A further hypothesis on the polyhedron of A. Dürer's engraving Melencolia I, Historia Mathematica, 31 (1): 11—14, doi:10.1016/S0315-0860(03)00029-6.
• Hideko, Ishizu (2009), Another solution to the polyhedron in Dürer's Melencolia: A visual demonstration of the Delian problem (PDF), Aesthetics, The Japanese Society for Aesthetics, 13: 179—194, архів оригіналу (PDF) за 19 лютого 2018, процитовано 18 травня 2020.
• Ziegler, Günter M. (3 грудня 2014), Dürer's polyhedron: 5 theories that explain Melencolia's crazy cube, The Guardian, архів оригіналу за 11 листопада 2020, процитовано 18 травня 2020.
• Futamura, F.; Frantz, M.; Crannell, A. (2014), The cross ratio as a shape parameter for Dürer's solid, Journal of Mathematics and the Arts, 8 (3-4): 111—119, arXiv:1405.6481, doi:10.1080/17513472.2014.974483.

Посилання

• Weisstein, Eric W. Dürer's Solid(англ.) на сайті Wolfram MathWorld.
• How to build Dürer's Polyhedron — by DUPLICON (in German) [Архівовано 30 вересня 2020 у Wayback Machine.]
• Open-source 3D models of Dürer's Solid