П'ятикутник

П'ятику́тник — планіметрична фігура, многокутник, що має п'ять сторін, п'ять вершин та п'ять кутів.
Також можливе альтернативне визначення:
П'ятику́тник — це частина площини, обмежена простою замкненою ламаною, яка містить п'ять ланок. Вона складається з п'яти точок (вершин п'ятикутника), послідовно з'єднаних п'ятьма відрізками (сторони або ребра п'ятикутника). При цьому жодні три з даних точок не повинні лежати на одній прямій.
П'ятикутник позначають, записуючи його вершини. Наприклад, так: ABCDE. У позначенні п'ятикутника вершини, що стоять поряд, повинні бути сусідніми.
Вершини п'ятикутника називаються сусідніми, якщо вони є кінцями однієї з його сторін. Відрізки, що сполучають несусідні вершини п'ятикутника, називаються діагоналями.
Сторони п'ятикутника, що виходять з однієї вершини, називаються сусідніми сторонами.
П'ятикутник може бути простим (без самоперетинів; може бути опуклим та вгнутим) або схрещеним[en](з самоперетином).
Сума довжин усіх сторін п'ятикутника називається периметром.
Сума внутрішніх кутів простого п'ятикутника дорівнює 540°.
Площа п'ятикутника без самоперетинів[ред. | ред. код]
Площа довільного п'ятикутника без самоперетинів, що заданий координатами своїх вершин, визначається за формулою площі Гаусса, загальною для багатокутників .
Опуклий п'ятикутник[ред. | ред. код]

Опуклим п'ятикутником називається такий п'ятикутник, всі точки якого лежать по один бік від будь-якої прямої, що проходить через дві його сусідні вершини.
Можливі також альтернативні визначення.
Опуклим п'ятикутником називається
— п'ятикутник, який обмежує опуклу множину. Тобто для будь-яких двох точок п'ятикутника відрізок, що їх з'єднує, повністю належить п'ятикутнику.
— п'ятикутник такий, що всі його діагоналі повністю лежать всередині нього.
Внутрішній кут опуклого п'ятикутника — кут між двома його сусідніми сторонами. Будь-який внутрішній кут опуклого п'ятикутника менше 180°.
Сума внутрішніх кутів опуклого п'ятикутника дорівнює радіан.
Зовнішній кут — кут, що суміжний внутрішньому.
Як і у всіх полігонів, сума зовнішніх кутів (по одному при кожній стороні) становить радіан.
Кількість діагоналей опуклого п'ятикутника (З кожної вершини можна провести 2 діагоналі). Діагоналі, що виходять з однієї вершини, розбивають п'ятикутник на 3 трикутники.
В усіх опуклих п'ятикутників, сума квадратів діагоналей є в три рази меншою за суму квадратів його сторін.[1]
Сума діагоналей S опуклого п'ятикутника більша за периметр, але менша за подвійний периметр:
Будь-які 9 точок у загальному положенні містять вершини опуклого п'ятикутника і існує множина з 8 точок у загальному положенні, в якій немає опуклого п'ятикутника.[2] Доведено також, що будь-які 10 точок на площині в загальному положенні містять порожній опуклий п'ятикутник (Тобто п'ятикутник, який не містить внутрішніх точок).(Harborth, 1978). І існує множина з 9 точок у загальному положенні, в якій немає порожнього опуклого п'ятикутника.
П'ятикутник вписаний в коло[ред. | ред. код]

П'ятикутник називається вписаним в деяке коло, якщо всі його вершини лежать на цьому колі. При цьому коло називається описаним навколо п'ятикутника.
Центр описаного навколо п'ятикутника кола лежить на перетині серединних перпендикулярів (або медіатрисах) до його сторін.
Сума будь-яких двох несуміжних кутів вписаного п'ятикутника більше 180°.
Аналог теореми сінусів для п'ятикутника: навколо п'ятикутника можна описати коло радіусом R, якщо виконуються наступні рівності:

R - радіус описаного кола.
Внутрішній кут вписаного п'ятикутника:
Кут між двома діагоналями, що виходять з однієї вершини можна знайти за формулою:
Вписаний п'ятикутник (як і будь-який вписаний багатокутник) можна розбити на рівнобедрені трикутники, вершини яких лежать в центрі описаного кола, а бокові сторони є радіусами кола, що проходять через його вершини.
Для довільного п'ятикутника ABCDE, у якого суми будь-яких несуміжних кутів більше 180°, існує п'ятикутник A'B'C'D'E' з такими ж кутами, навколо якого можна описати коло.
Для довільного п'ятикутника ABCDE, існує п'ятикутник A'B'C'D'E' з такими ж сторонами, навколо якого можна описати коло.
Площу будь-якого вписаного п'ятикутника можна знайти як 14 квадратного кореня з одного з коренів рівняння 7-го степеня[en] , коефіцієнти якого є функціями сторін п'ятикутника.[3][4][5]
Існують вписані п'ятикутники з раціональними сторонами і раціональною площею; їх називають п'ятикутниками Роббінса[en]. У всіх відомих випадках його діагоналі також мають раціональні довжини. Було доведено, що всі діагоналі п'ятикутника Роббінса повинні бути або раціональними, або всі ірраціональними, і є припущення, що всі діагоналі - раціональні. [6]
Точка на описаному колі[ред. | ред. код]
Нехай точка М лежить на дузі описаного кола одиничного радіуса між вершинами А і В. Тоді виконується нерівність [7]:
П'ятикутник описаний навколо кола[ред. | ред. код]
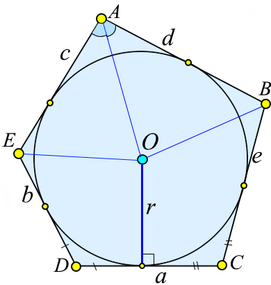
П'ятикутник називається описаним навколо деякого кола, якщо це коло дотикається до всіх сторін п'ятикутника. При цьому коло називається вписаним в п'ятикутник.
Центр вписаного в п'ятикутник кола лежить на перетині бісектрис його внутрішніх кутів. І навпаки, якщо всі бісектриси внутрішніх кутів деякого п'ятикутника перетинаються в одній точці, то в цей п'ятикутник можна вписати коло з центром в цій точці.
Сума будь-яких двох несусідних сторін описаного п'ятикутника менша від суми трьох інших сторін.
В п'ятикутник можна вписати коло радіусом r, якщо виконуються наступні рівності:
Коло вписано в п'ятикутник зі сторонами a, b, c, d і e. Відрізки, на які точка дотику ділить сторону а:
та
Радіус вписаного кола[8]:
де S - площа п'ятикутника, p - півпериметр.
Для довільного п'ятикутника ABCDE, для якого сума будь-яких двох несусідних сторін менше суми трьох інших сторін, існує п'ятикутник A'B'C'D'E' з такими ж сторонами, в який можна вписати коло.
Для довільного опуклого п'ятикутника існує п'ятикутник з такими ж кутами, в який можна вписати коло.
Описаний п'ятикутник має найбільшу площу серед п'ятикутників з тим же периметром і такими ж внутрішніми кутами взятими в тій самій послідовності.[9][10]
Описаний п'ятикутник має всі рівні сторони лише у випадку, коли всі його внутрішні кути також рівні; тобто це правильний п'ятикутник.
Рівносторонні п'ятикутники[ред. | ред. код]

Рівносторонній п'ятикутник[en] це п'ятикутник зі сторонами однакової довжини. Однак, його внутрішні кути можуть приймати різні значення, таким чином це ціла родина п'ятикутників.
Чотири рівних кола, що перетинаються, розташованих у замкнутий ланцюг, однозначно визначають деякий опуклий рівносторонній п'ятикутник. Центр кожного кола є однією з чотирьох вершин п'ятикутника і лежить на сусідньому колі. П'ята вершина визначається однією з точок перетину першого і останнього кола ланцюга. Деякі приклади рівносторонніх п'ятикутників:
-
Опуклий п'ятикутник
-
Неопуклий (вгнутий) п'ятикутник
-
Схрещений п'ятикутник (з самоперетинами)
-
Вироджений п'ятикутник (вершина лежить на ребрі)
Правильний п'ятикутник[ред. | ред. код]

Правильний п'ятикутник (пентагон) — це правильний багатокутник з п'ятьма сторонами.
Правильний п'ятикутник — опуклий п'ятикутник, у якого всі сторони і кути рівні.
Внутрішній кут правильного п'ятикутника дорівнює 108. Центральний кут дорівнює 72.
Правильний п'ятикутник є унікальним (в межах подібності), оскільки він рівносторонній, і всі його п'ять кутів рівні між собою. Він є вписаним і описаним одночасно.
Правильний п'ятикутник має п'ять ліній дзеркальної симетрії, і обертову симетрію 5-го порядку (у 72°, 144°, 216° і 288°). Центру симетрії не має.
Правильний багатокутник сторони якого перетинаються (або зірковий п'ятикутник) називається пентаграмою.
Паркети з п'ятикутників[ред. | ред. код]

Правильний п'ятикутник не може з'являтися в жодій мозаїці, складеній з правильних багатокутників.
По-перше, п’ятикутник не може утворювати регулярну мозаїку (у якій усі грані конгруентні, тому всі багатокутники повинні бути правильними п’ятикутниками). Зауважимо, що 360° / 108° = 31⁄3 (де 108° — внутрішній кут) , яке не є цілим числом; отже, не існує цілого числа правильних п'ятикутників, які мають одну вершину і не залишають проміжків між ними.
Найкраще відоме замощення площини правильними п'ятикутниками має щільність пакування[en] і утворює подвійну ґратку
У препринті, опублікованому в 2016 році, американські математики Томас Хейлз[en] і Воден Куснер оголосили про доказ того, що ця подвійна гратчаста упаковка правильного п’ятикутника має оптимальну щільність серед усіх упаковок правильних п'ятикутників на площині.[11].
Станом на 2022 рік їх підтвердження ще не було опубліковано в рецензованому журналі.
Складніше довести, що п’ятикутник не може бути в будь-якій мозаїці від краю до краю, утвореній правильними багатокутниками:
Також не існує комбінацій із 4 або більше правильних багатокутників, що зустрічаються у вершині, яка містить п’ятикутник. Для комбінацій із 3: якщо 3 багатокутники зустрічаються у вершині і один має непарну кількість сторін, інші 2 мають бути конгруентними. Причина цього в тому, що багатокутники, які торкаються сторін п'ятикутника, повинні чергуватися навколо п'ятикутника, що неможливо через непарну кількість його сторін. Для п’ятикутника це дає багатокутник, усі кути якого дорівнюють (360 − 108) / 2 = 126°. Кількість сторін цього многокутника дорівнює 360 / (180 − 126) = 62⁄3, що не є цілим числом. Тому п'ятикутник не може з'явитися в будь-якій мозаїці, складеній з правильних багатокутників.
Існує 15 класів неправильних опуклих п'ятикутників[12] , які утворюють п'ятикутний паркет[en], тобто можуть замостити площину своїми копіями без проміжків та накладень. Жоден з п'ятикутників не має симетрії в цілому, хоча деякі мають окремі випадки з дзеркальної симетрії. Останній з них було знайдено в 2015 році.[13]
| 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|

|

|

|

|

|
| 6 | 7 | 8 | 9 | 10 |

|

|

|

|

|
| 11 | 12 | 13 | 14 | 15 |

|

|

|

|

|
Графи[ред. | ред. код]
K5 повний граф часто малюють як правильний п'ятикутник що має всі 10 з'єднаних ребер. Цей граф також представляє ортографічну проєкцію 5-ти вершин і 10-ти ребер 5-комірника. Зрізаний 5-комірник, із вершинами на внутрішніх ребрах 5-комірника проектується в середині п'ятикутника.
 5-комірник (4 виміри) |
 Зрізаний 5-комірник (4 виміри) |
П'ятикутники в природі[ред. | ред. код]
Рослини[ред. | ред. код]
-
П'ятикутний переріз окри.
-
Квітка кручених паничів, як і багато інших квітів, має п'ятикутну форму.
-
Карамболя ще один приклад п'ятірчастої симетрії.
Тварини[ред. | ред. код]
-
Морська зірка. Багато голкошкірих мають п'ятірчасту радіальну симетрію.
-
Ілюстрація змієхвістки, також голкошкірого організму з п'ятикутною формою.
Рукотворні[ред. | ред. код]
-
Пентагон, штаб-квартира Міністерства оборони США.
-
Плита для позначення бази на бейзбольному полі.
П'ятикутник в основі багатогранників[ред. | ред. код]
| Ih[en] | Th[en] | Td[en] | O[en] | I[en] | D5d[en] |
|---|---|---|---|---|---|

|

|

|

|

|

|
| Додекаедр | Піритоедр[en] | Тетатроід[en] | Пентагональний ікосітетраедр[en] | Пентагональний гексеконтаедр[en] | Зрізаний трапецоедр[en] |
Див. також[ред. | ред. код]
Примітки[ред. | ред. код]
- ↑ Inequalities proposed in «Crux Mathematicorum», [1].
- ↑ Kalbfleisch, J.D.; Kalbfleisch, J.G. & Stanton, R.G. (1970). A combinatorial problem on convex regions, vol. 1 (англ.) . Louisiana State Univ.: Proc. Louisiana Conf. Combinatorics, Graph Theory and Computing. с. pp. 180-188.
{{cite book}}:|pages=має зайвий текст (довідка) - ↑ Weisstein, Eric W. "Cyclic Pentagon." From MathWorld--A Wolfram Web Resource. [2]
- ↑ Robbins, D. P. (1994). Areas of Polygons Inscribed in a Circle. Discrete and Computational Geometry. 12 (2): 223—236. doi:10.1007/bf02574377.
- ↑ Robbins, D. P. (1995). Areas of Polygons Inscribed in a Circle. The American Mathematical Monthly. 102 (6): 523—530. doi:10.2307/2974766. JSTOR 2974766.
- ↑ Buchholz, Ralph H.; MacDougall, James A. (2008). Cyclic polygons with rational sides and area (англ) . Journal of Number Theory. с. 128: 17–48. doi:10.1016/j.jnt.2007.05.005. MR 2382768.
- ↑ Inequalities proposed in Crux Mathematicorum (PDF). The IMO Compendium. p. 190, #332.10.
- ↑ Alsina, Claudi and Nelsen, Roger, Icons of Mathematics. An exploration of twenty key images, Mathematical Association of America, 2011, p. 125.
- ↑ Tom M. Apostol and Mamikon A. Mnatsakanian (December 2004). Figures Circumscribing Circles (PDF). American Mathematical Monthly. 111 (10): 853—863. doi:10.2307/4145094. JSTOR 4145094. Процитовано 6 квітня 2016.
- ↑ Apostol, Tom (December 2005). erratum. American Mathematical Monthly. 112 (10): 946. doi:10.1080/00029890.2005.11920274. S2CID 218547110.
- ↑ Hales, Thomas; Kusner, Wöden (September 2016), Packings of regular pentagons in the plane, arXiv:1602.07220
- ↑ Grünbaum, Branko; Shephard, Geoffrey C. (1987). "Tilings by polygons" (англ.) . New York: W. H. Freeman and Company. ISBN 978-0-7167-1193-3. MR 0857454.
- ↑ Mann, Casey; McLoud-Mann, Jennifer; Von Derau, David (2018). "Convex pentagons that admit i-block transitive tilings" (англ.) . Geometriae Dedicata. с. 194 (1): 141–167. arXiv:1510.01186. doi:10.1007/s10711-017-0270-9.
Джерела[ред. | ред. код]
- Harborth, Heiko (1978). Konvexe Fünfecke in ebenen Punktmengen. Elem. Math. 33 (5): 116–118..
Посилання[ред. | ред. код]
| Основні опуклі правильні й однорідні політопи в розмірностях 2-10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Родина | An | Bn | I₂(p) / Dn | E₆ / E₇ / E₈ / F₄ / G₂ | Hn | |||||||
| Правильний многокутник | Правильний трикутник | Квадрат | p-кутник | Правильний шестикутник | Правильний п'ятикутник | |||||||
| Однорідний многогранник | Правильний тетраедр | Правильний октаедр • Куб | Півкуб | Правильний додекаедр • Правильний ікосаедр | ||||||||
| Однорідний 4-політоп | П'ятикомірник | 16-комірник • Тесеракт | Півтесеракт | 24-комірник | 120-комірник • 600-комірник | |||||||
| Однорідний 5-політоп | Правильний 5-симплекс | 5-ортоплекс • 5-гіперкуб | 5-півгіперкуб | |||||||||
| Однорідний 6-політоп | Правильний 6-симплекс | 6-ортоплекс • 6-гіперкуб | 6-півгіперкуб | 122 • 221 | ||||||||
| Однорідний 7-політоп | Правильний 7-симплекс | 7-ортоплекс • 7-гіперкуб | 7-півгіперкуб | 132 • 231 • 321 | ||||||||
| Однорідний 8-політоп | Правильний 8-симплекс | 8-ортоплекс • 8-гіперкуб | 8-півгіперкуб | 142 • 241 • 421 | ||||||||
| Однорідний 9-політоп | Правильний 9-симплекс | 9-ортоплекс • 9-гіперкуб | 9-півгіперкуб | |||||||||
| Однорідний 10-політоп | Правильний 10-симплекс | 10-ортоплекс • 10-гіперкуб | 10-півгіперкуб | |||||||||
| Однорідний n-політоп | Правильный n-симплекс | n-ортоплекс • n-гіперкуб | n-півгіперкуб | 1k2 • 2k1 • k21 | n-п'ятикутний многогранник | |||||||
| Topics: Родини політопів • Правильні політопи • Список правильних політопів і з'єднань | ||||||||||||