Стала Планка

Значення h	Одиниці
6.62606957(29)×10−34	Дж·с
4.135667516(91)×10−15	еВ·с
6.62606957(29)×10−27	ерг·с
Значення ħ	Одиниці
1.054571726(47)×10−34	Дж·с
6.58211928(15)×10−16	еВ·с
1.054571726(47)×10−27	ерг·с

Пам'ятний знак Максові Планку на честь відкриття ним сталої Планка, на фасаді Гумбольдтівського університету, Берлін. Напис гласить: «В цій будівлі викладав Макс Планк, який винайшов елементарний квант дії h, з 1889 по 1928».

Стала Планка — елементарний квант дії, фундаментальна фізична величина, яка відображає квантову природу Всесвіту. Загальний момент кількості руху фізичної системи може змінюватись лише кратно величині сталої Планка. Як наслікок у квантовій механіці фізичні величини виражаються через сталу Планка.

Стала Планка позначається латинською літерою h. Вона має розмірність енергії, помноженої на час.

Частіше використовується зведена стала Планка

$\hbar = \frac{h}{2\pi}$.

Крім того, що вона зручніша для використання в формулах квантової механіки, вона має особливе позначення, яке ні з чим не сплутаєш.

Числове значення

У системі СІ стала Планка має таке значення:

• $h=6.62606957(29) \times10^{-34} \,$ Дж · с

Для розрахунків у квантовій фізиці зручніше використовувати значення зведеної сталої Планка, виражене через електронвольти.

• $\hbar=6.58211928(15) \times 10^{-16} \,$ еВ · с.

Історія

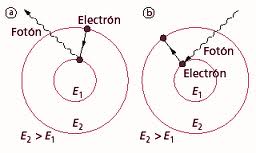
Макс Планк ввів свою сталу для пояснення спектру випромінювання абсолютно чорного тіла, припустивши, що тіло випромінює електромагнітні хвилі порціями (квантами) з енергією, пропорційною частоті ($h\nu$). У 1905 році Ейнштейн використав це припущення для того, щоб пояснити явище фотоефекту, постулювавши, що електромагнітні хвилі поглинаються порціями з енергією пропорційною частоті. Так зародилася квантова механіка, в справедливості якої обидва лауреати Нобелівської премії сумнівалися все життя.

Посилання

• Посилання NIST щодо констант, одиниць виміру, неточностей (CODATA 2010) (англ.)
• Історія уточнення сталої Планка (рос.)