Хвиля
| Хвиля | |
 | |
 | |
| |

Хви́ля — існує кілька визначень хвилі:
- хвиля — зміна стану середовища (збурення), яке поширюється в просторі й переносить енергію. В багатьох випадках з поширенням хвиль пов'язано передачу інформації.
- хвиля — процес розповсюдження коливань у будь-якому фізичному середовищі. Хвильовий процес — процес передачі коливань. При цьому частинки середовища не рухаються разом з хвилею, а коливаються навколо своїх положень рівноваги[2]. Середовищем, у якому поширюються хвилі може бути як речовина, так і вакуум, наприклад, у випадку електромагнітних хвиль. У вакуумі поширюються також недавно зафіксовані гравітаційні хвилі. Залежно від характеру руху частинок середовища при поширенні розрізняють наступні типи хвиль: поздовжні, поперечні, а також хвилі на поверхні води та на поверхні пружного тіла. У цих двох останніх хвилях рух частинок середовища відбувається по більш складних траєкторіях (хвиля Релея[en])[3].
Хвилі характеризують величиною збурення — амплітудою й напрямком поширення. Швидкість поширення хвилі визначається властивостями середовища та геометрією області існування хвильового збурення і не пов'язана зі швидкістю руху частинок середовища при передачі збурень. Хвилі одного типу з різними рівнями збурень (різні локальні швидкості руху частинок середовища) поширюються з однаковою швидкістю. Часто при описі хвильових рухів для швидкості поширення збурень використовують поняття швидкість звуку або швидкість світла.
Хвильові збурення виникають під час руху тіл в рідинах та газах та при нестаціонарному навантаженні пружних тіл. Затратами енергії на формування хвильових збурень визначається величина хвильового опору.
Поняття хвилі (хвильового руху) є фундаментальним поняттям фізики, розуміння змісту якого необхідне при аналізі широкого кола явищ в сучасному світі. Як відмічено на сайті Хвилі: світло, звук та природа реальності",,,щоб зрозуміти світло, звук і саму природу реальності, потрібно спочатку розібратися в хвилях"[4],
Навколишній світ заповнений хвильовими рухами, які вражають своїм різноманіттям. Список лише тих хвильових явищ, які відзначені в фізиці іменами своїх першовідкривачів чи дослідників включає видатні імена. Це хвилі Альвена, Блоха, Д'яконова, Гуляєва-Блюстейна, Фарадея. Герстнера, Кельвіна, Лемба, Ленгмюра, Лява, Маха, Релея, Росби, Стокса, Толмина-Шлихтинга. Такі хвильові процеси реалізуватися в різних фізичних середовищах і з різними масштабами.
Вступ[ред. | ред. код]
Поняття «хвиля» широко застосовується в повсякденному житті та в багатьох розділах природознавства[5] Це зумовлено тим, що в процесах розповсюдження збурень у різних середовищах і у вакуумі є багато спільних рис. Хвилі можна, наприклад, утворити на поверхні води або на довгій мотузці. Поширення хвиль не супроводжується перенесенням частинок середовища, вони коливаються тільки біля свого положення рівноваги. При певних умовах можна спостерігати процес передачі енергії хвильового руху в кінетичну енергію потоку. Таке явище чітко видно при руйнуванні поверхневої хвилі на воді при набіганні її на берег або іншу перешкоду. Спостерігаючи за стрімким потоком води в річці можна бачити і зворотний процес переходу кінетичної енергії потоку в енергію хвильового руху.
Твердження про відсутність переносу частинок рідини в поверхневій хвилі вимагає певного уточнення. Таке твердження було зроблено на основі аналізу руху частинок у рідині за формулами, що одержані в лінійному наближенні. Більш детальний нелінійний аналіз процесу поширення поверхневих хвиль на воді виконано в середині XIX століття англійським вченим Г. Стоксом. Він встановив, що частинки рідини при поширенні поверхневої хвилі рухаються незамкненими траєкторіями, відбувається певний дрейф частинок рідини. Ним же була встановлена формула для швидкості цього дрейфу [6] . Тут — амплітуда хвилі, — хвильове число, — кругова частота і — відстань від поверхні частинки рідини. Траєкторії руху частинок рідини при поширенні поверхневої хвилі з урахуванням нелінійності показано на рисунку. При спостереженні за хвильовими рухами в реальних умовах ситуація дещо ускладнюється наявністю вітру, який теж генерує горизонтальний рух частинок рідини. Для хвиль, що генеруються вітром, виконано досить багато досліджень, спрямованих на пошук кількісних оцінок величини дрейфу. За результатами роботи[7] для оцінки порядку величини середньої швидкості дрейфу можна вважати .

У загальному випадку хвилі не обов'язково пов'язані з наявністю речовини. Електромагнітні хвилі у вакуумі є взаємозалежними змінами електричних і магнітних полів, а гравітаційні хвилі є змінами геометрії простору-часу. У таких речовинах, як рідини, гази та тверді пружні тіла поширення збурень супроводжується специфічним рухом частинок середовища. Цей рух забезпечує передачу в просторі збурень без переносу речовини. При розгляді електромагнітних хвиль слід мати на увазі корпускулярно-хвильовий дуалізм, що є основою квантової механіки. Згідно з ним, будь-яка частинка має хвильові властивості, а хвилі випромінюються й поглинаються скінченними порціями — квантами. Однак багато фундаментальних понять для опису хвильових процесів є спільними для всіх типів хвиль. У зв'язку з цим теорія хвиль сформувалася як розділ сучасної фізики, пов'язаний із вивченням властивостей хвиль незалежно від їх фізичної природи. Конкретні приклади для пояснення змісту цих понять у цій статті будуть пов'язані з механічними хвилями.
Загальні властивості[ред. | ред. код]
Наповнення конкретним змістом понять, що застосовуються для опису хвильових явищ, базується на використанні математичних моделей конкретних природних об'єктів. Застосовуються як дискретні моделі, в яких об'єкт замінюється сукупністю частинок, так і моделі суцільного середовища. Фізичною основою для виникнення хвильових рухів, тобто переносу збурень від одного місця до іншого, є наявність двох факторів — будь-яка частинка середовища має певну масу і при відхиленні частинки з положення рівноваги (під дією зовнішніх сил) у результаті взаємодії між частинками виникає сила, що намагається повернути її в положення рівноваги. У результаті частинка починає рухатися до положення рівноваги, збуджуючи сусідні частинки середовища. Так виникає рух, що зумовлює перенос стану і, відповідно, енергії до іншої частини середовища. Самі частинки середовища можуть здійснювати досить складні рухи, але врешті-решт повертаються до положення рівноваги. У реальних середовищах при передачі збурень від однієї частинки до іншої частина внесеної початковим збуренням енергії втрачається, переходячи в тепло. Однак у багатьох випадках при вивченні хвильових рухів ці втрати незначні (за проміжок часу, який характерний для хвильового процесу) і не враховуються. Для характеристики хвильових збурень різної фізичної природи застосовують такі поняття як швидкість розповсюдження, напрям, потік енергії. При цьому між напрямком переносу енергії та характером руху частинок середовища немає прямого зв'язку. Що стосується терміну «швидкість хвилі», то фізично обґрунтоване вживання цього терміну можливе лише щодо хвиль, які при розповсюдженні не змінюють форму (див. дисперсія хвилі). Велике значення для аналізу хвильових процесів має факт існування притаманних їм внутрішніх просторових та часових масштабів, якими є довжина хвилі та її період.
Закономірності переносу збурень у середовищі суттєво залежать від відносної величини збурень. У зв'язку з цим розрізняють два принципово відмінних типи хвиль — лінійні й нелінійні хвилі. Для визначення масштабу збурень слід глибоко вивчити властивості середовища, в якому розглядається процес переносу збурень і, перш за все, особливості сил, що визначають взаємодію частинок середовища. Для лінійних хвиль швидкість переносу збурень визначається лише фізичними властивостями речовини середовища та геометрією області, в якій збурення розповсюджуються. Граничним значенням для швидкості переносу енергії в будь якому середовищі є швидкість електромагнітних хвиль у вакуумі (швидкість світла).
Вивчаючи хвильові явища в різних середовищах ми маємо справу з проявами рухів, що характеризуються величезною різницею в масштабах від мікро- до макро- явищ. Так, до хвильових рухів належать хвилі-вбивці на поверхні океану, висота яких може сягати декількох десятків метрів, а також звукові хвилі, за допомогою яких відбувається спілкування між людьми та іншими живими істотами. При передачі інформації пошепки амплітуда зміщень частинок повітря становить усього см. Така різниця характерна не лише для амплітуд збурень, але і для таких характеристик як довжина хвилі, характерна частота, швидкість переносу енергії збурення, швидкість руху частинок середовища. Так, найменша частота, що сприймається людським вухом як звук, становить 20 Гц. У той час як характерна частота світлових (електромагнітних) хвиль становить Гц.
Особливості руху частинок середовища, в якому поширюються хвильові збурення, зумовлюють деякі специфічні хвильові ефекти, що супроводжують процеси генерації, поширення хвиль та їх взаємодії з перешкодами. Серед них слід відзначити ефекти дифракції, рефракції, розсіювання, дисперсії, трансформації одного типу хвильового руху в інший (поздовжніх хвиль у поперечні) та ін.
Різновиди хвиль[ред. | ред. код]
За характером розповсюдження розрізняють стоячі (стійні, нерухомі) й біжучі (біжні) хвилі.
За періодичністю — періодичні й неперіодичні (у граничному випадку — самотні хвилі, солітони).
За типом коливань — поперечні, поздовжні та змішані.
За законами, які описують хвильовий процес: лінійні й нелінійні.
При розгляді збурень на поверхні води виділяють хвилі за характером дії збурення — вітрові хвилі, корабельні хвилі. Серед хвиль на воді особливо виділяють цунамі та хвилі-вбивці. За характером відновлювальної сили. Всі ці хвилі є гравітаційними. В таких складних середовищах, як океани чи земна атмосфера, фізичні властивості суттєво змінюються з глибиною (висотою). У зв'язку з цим в них можуть виникати гравітаційні хвилі, що локалізуються в шарах на різних відстанях від границь. Такі хвилі називають внутрішніми хвилями.
Залежно від геометричної форми фронту хвилі поділяють на плоскі, сферичні, циліндричні, хоча у випадку розсіювання на перешкодах фронт хвилі може набувати складної просторової форми.
Математичний опис одновимірних хвиль[ред. | ред. код]
Математичні співвідношення для опису хвиль в різного типу матеріальних середовищах базуються на фундаментальному законі сучасної нерелятивістської механіки — на другому законі Ньютона, що формулюється щодо певного елемента середовища. Його маса визначається густиною середовища, а відновлювальна сила визначається характером взаємодії між його частинками. Зв'язок між силовими факторами та деформаціями, що характеризують зміну відстані між частинками середовища або форми елементарного об'єму, описується характерним для цього середовища рівнянням стану. При моделюванні реальних середовищ під час вивчення рухів, пов'язаних із переносом маси, часто застосовують модель нестисливого середовища, тобто середовища, в якому силовим впливом неможливо змінити об'єм виділеного елемента. У такому модельному середовищі хвилі не існують.
Як видно з наведеного вище зображення хвиль за кораблями, просторова структура збурень може бути досить складною. Тому вивчення особливостей хвильових рухів починають з розгляду найпростіших модельних ситуацій, так званих одновимірних хвиль, коли частинка середовища в цілому, або розташована на характерної прямій в ньому, при виникненні збурень може рухатися лише в одному напрямку. У такому випадку всі характеристики хвилі залежать від часу та однієї просторової координати. Така ситуація може виникнути при розповсюдженні плоских хвиль у нескінченному середовищі. Більш реальними є випадки, коли збурення поширюється в струні чи тонкому пружному стрижні. Одновимірною є також сферично-симетрична хвиля.
При побудові математичних моделей хвильових явищ завжди застосовують певні модельні припущення відносно об'єкту, в якому хвилі розповсюджуються. Так, говорячи про струну, вважають її нескінченно тонкою лінією, будь-який відрізок якої має певну масу. Відновлювальна сила, що виникає при відхиленні точок струни від положення рівноваги, забезпечується силою, що прикладена вздовж струни (попередній натяг) і вважається сталою. Таким чином такий модельний об'єкт, як струна, характеризується двома фізичними параметрами: лінійна густина , що має розмірність [кг/м], та попереднім натягом , що вимірюється в ньютонах. Фізичною величиною, що описує поширення збурень у струні є величина зміщень точок струни перпендикулярно до положення рівноваги. Це зміщення описується функцією координати та часу .
Співвідношення другого закону Ньютона для елемента струни приводять до наступного диференціального рівняння в частинних похідних:[8]
-
()
Тут . Важливо пам'ятати, що при отриманні цього рівняння зроблено припущення:
Це суттєве обмеження на ступінь гладкості збурень у струні. Якщо ця вимога не виконується, у рівнянні руху елементу струни з'являються нелінійні складові. Хвилі стають нелінійними. Цей приклад дозволяє сформулювати важливу вимогу до використання математичних моделей у фізичних проблемах: завжди пам'ятати про припущення, зроблені під час отримання рівнянь, і в постановці конкретних граничних задач при виборі форми початкових збурень не виходити за межі зроблених припущень.
До такого ж рівняння (1) призводить вивчення поздовжніх хвиль у пружному стержні. Так зазвичай називають циліндричне пружне тіло, у якого розмір поперечного перерізу значно менший довжини. Якщо зсув точок стрижня вздовж осі описувати за допомогою функції , то співвідношення другого закону Ньютона разом із законом пружності Гука приводять до рівняння[8]:
Тут , де модуль пружності Юнга, а густина матеріалу стрижня.
Хвилі в тонкому пружному стрижні, в якому початкові збурення викликають деформації згинання, за певних припущень[8] теж можна описати функцією , яка визначає відхилення точок осі стрижня від положення рівноваги. За фізичним змістом ця функція не відрізняється від функції, що описує рух хвиль у струні. Однак, рівняння руху елементу стрижня відрізняється від наведеного вище для струни й має вигляд:
-
()
Фізичною причиною таких відмінностей є наявність згинної жорсткості в пружному стрижні.
І в першому, і в другому рівнянні величина має розмірність швидкості, однак фізичний зміст цих величин суттєво відрізняється[8]. Суттєво відрізняються й властивості хвиль, що розповсюджуються в цих об'єктах. Ця різниця аналізується в наступних розділах.
Хвильове рівняння[ред. | ред. код]
Рівняння (1), що описує розповсюдження збурень у струні, є частковим випадком загального рівняння в частинних похідних, яке називається хвильовим рівнянням. Для збурень в тривимірному середовищі хвильове рівняння в декартових координатах записується у вигляді:
-
()
Фізичний зміст введеної функції може бути різним залежно від фізичних властивостей середовища. Це може бути потенціал швидкостей точок середовища або збурення тиску. Рівняння такого типу належать до рівнянь гіперболічного типу і всебічно вивчаються математичною фізикою[9]. На першому малюнку показано поверхневі гравітаційні хвилі на воді. Характер руху в таких хвилях можна описати з допомогою потенціалу швидкостей . Однак, для такого типу збурень стисливість води виявляється несуттєвою[10].
За такої умови загальне хвильове рівняння зводиться до рівнянням Лапласа (права частина в (3) покладається рівною нулю).
Побудова розв'язків граничних задач із заданими початковими умовами для таких рівнянь у загальному випадку є досить складною проблемою. Однак, для одновимірного збурення, яке описується рівнянням (1), маємо унікальну ситуацію, коли вдається побудувати загальний розв'язок рівняння. Це рівняння було вперше отримано французьким математиком д'Аламбером 1747 року. Він же подав його загальний розв'язок у вигляді:
-
()
Тут і довільні двічі диференційовні функції від вказаних специфічних аргументів. Розв'язок д'Аламбера вказує на принципову особливість хвильового рівняння — сума будь-яких двох розв'язків є також розв'язком рівняння. Це частинний випадок принципу суперпозиції, що характерний для всіх лінійних задач математичної фізики. Для певної конкретної форми функції зміна її в часі показана на рисунку. Видно, що ця функція описує розповсюдження збурення в струні в додатному напрямку осі . Другий доданок в рівнянні (4), очевидно, описує збурення, що розповсюджується в від'ємному напрямку осі . Таким чином, у загальному випадку будь-які збурення в струні являють собою суму (суперпозицію) двох збурень, що розповсюджуються в протилежних напрямках. Конкретна форма збурень визначається початковими умовами.

На рисунку представлено зображення відрізку струни в два різні моменти часу. Видно, що збурення пересувається вправо без зміни форми зі швидкістю і саме цією швидкістю визначається відстань між точками, що перебувають в однаковій фазі відхилення від положення рівноваги. Саме цьому ця швидкість називається фазовою швидкістю хвилі. Графічна ілюстрація до визначення поняття фазової швидкості дозволяє звернути увагу на цікаву особливість хвильового руху в нескінченній струні. Як видно, точки струни, виведені з положення рівноваги зміщенням у додатному напрямку вертикальної осі, ніколи не перейдуть через положення рівноваги.
Форми хвилі[ред. | ред. код]
Форма хвилі, тобто просторовий розподіл збурень, визначається кількома факторами, зокрема, просторовим розподілом початкових збурень, властивостями середовища, в якому збурення розповсюджуються, геометричними особливостями області, заповненої середовищем. У деяких випадках, одновимірні хвилі, плоскі хвилі, у процесі розповсюдження збурень форма хвилі не змінюється. Як показано на малюнку говорячи про форму збурення для хвиль, що описуються рівнянням (1), можна дати простір уяві.

Однак слід мати на увазі, що така творча робота має досить формальний характер, оскільки рівняння (1) отримано з використанням певних припущень і наявність різного типу зломів у формах хвиль суперечить зробленим припущенням.
Найбільш цікавими при вивченні хвильових рухів є спеціальні типи хвиль, що виникають при певній часовій залежності їх характеристик. Це так звані гармонічні хвилі, в яких характеристики хвилі змінюються періодично. Як видно з загального розв'язку хвильового рівняння задана часова залежність визначає й залежність координатну. З представлення д'Ламбера випливає такий розв'язок для одновимірних гармонічних хвиль:
-
()
Тут параметр називається круговою частотою, а величина — хвильове число, визначається рівністю . Величини та називаються амплітудами гармонічних хвиль. Для часових характеристик гармонічної хвилі використовують три параметри: період коливань — , що вимірюється в секундах, кругову частоту , що вимірюється в радіанах на секунду, та частоту , що вимірюється в герцах. Між цими двома частотами має місце співвідношення .
У таких особливих хвилях збурення в кожній фіксованій точці змінюється періодично в часі. На рисунку показано рух певної точки струни при розповсюдженні гармонічної хвилі.

Так само в фіксований момент часу збурення в гармонічній хвилі є періодичною функцією координати. Великий інтерес до таких періодичних хвиль зумовлено тим, що у вигляді суперпозиції таких періодичних функцій можна подати будь-яку функцію часу чи просторової координати (ряди чи інтеграли Фур'є). При аналізі розповсюдження гармонічних хвиль формуються основні поняття хвильової динаміки.
Розглянемо для конкретності складову в (5), яка визначає хвилю, що біжить у додатному напрямку осі : Якщо спостерігати за певним відрізком струни, то побачимо таку картину зміни в часі стану цього відрізка, яка показана на анімаційному малюнку.

Відстань між двома точками, які перебувають в однаковій фазі збурення (наприклад, між послідовними максимумами чи мінімумами) називають довжиною хвилі. Якщо використати традиційне позначення для цієї характеристики , то з виразу для випливає співвідношення . Слід відзначити, що поняття довжини хвилі доцільно вживати лише для гармонічних хвиль. При розповсюдженні хвилі рідко переноситься речовина. Хвильовий процес пов'язаний з переносом енергії. Повний розгляд питання про потік енергії в одновимірній гармонічній хвилі базується на дещо громіздких викладках[8]. Позначаючи потік енергії в напрямку розповсюдження хвилі , маємо
. Це співвідношення справедливе для будь-якої хвилі в струні. Для гармонічної хвилі , що біжить у додатному напрямку осі для потоку енергії маємо вираз . Для фіксованої точки струни цей потік змінюється в часі, але завжди більший або дорівнює нулю. Важливо, що величина потоку є квадратичною функцією щодо збурення й тому принцип суперпозиції не працює під час розгляду енергетичних характеристик хвильових збурень, які складаються з декількох різних хвиль. Величина потоку енергії може бути як більшою, так і меншою суми енергій, що переноситься кожною хвилею окремо.
Модуляція[ред. | ред. код]
Загальний вираз для опису зміни в часі й по координаті певного параметру одновимірної гармонічної хвилі має вигляд:. Параметри, що визначають властивості хвилі, амплітуда , частота ,фаза вважаються сталими. Така хвиля не може передати інформацію. Для передачі корисної інформації застосовують різні методи зміни параметрів гармонічної хвилі. Такий процес зміни параметрів гармонічної хвилі називають модуляцією. Залежно від того, який параметр змінюється під час формування корисного сигналу розрізняють амплітудну модуляцію, частотну модуляцію та фазову модуляцію.
Фазова швидкість і групова швидкість[ред. | ред. код]
Як видно з виразів, що описують хвильові процеси в струні, при зміні частоти змінюється лише довжина хвилі, але фазова швидкість залишається незмінною. Ця обставина зумовлює те, що в струні енергія збурення переноситься з цією незмінною фазовою швидкістю незалежно від форми збурення. Однак, для багатьох хвильових процесів спостерігається інша поведінка хвиль. Найпростіший випадок одновимірного хвильового руху, який не має такої властивості, пов'язаний зі згинними хвилями в пружному стрижні. Рівняння для опису хвиль у ньому має вигляд[8]:
.
Тут — відхилення точок осі стрижня відносно положення рівноваги, які часто називають прогином. Для цього рівняння не існує загального розв'язку у формі д'Аламбера. Однак, у стрижні можуть розповсюджуватися гармонічні хвилі. Якщо шукану функцію прогину стрижня подати у вигляді , то для амплітудних значень збурень одержимо звичайне диференціальне рівняння . Якщо для зручності запровадити позначення його загальний розв'язок набуває виду
-
. ()
Враховуючи прийняту часову залежність для збурень та формулу Ейлера для комплексної експоненти знаходимо, що в стрижні справді існують розв'язки у вигляді хвиль, які біжать у протилежних напрямках, . І хоча зовні цей вираз нагадує розв'язок д'Аламбера для струни, тут маємо справу з принципово іншими хвилями. Різниця між гармонічними хвилями в струні й у стрижні виявляється під час визначення фазової швидкості. Якщо у разі струни ця швидкість не залежала від частоти, то з врахуванням прийнятих позначень маємо . Фазова швидкість цих хвиль залежить від частоти. Це явище залежності фазової швидкості від частоти в теорії хвильових рухів називають дисперсією хвиль. Розрізняють два типи дисперсії. Зменшення фазової швидкості з частотою характеризує нормальну дисперсію. У разі зростання фазової швидкості з частотою кажуть про аномальну дисперсію. В даному випадку згинних хвиль в пружному стрижні маємо хвилі з аномальною дисперсією. Дисперсія хвильових рухів може бути зумовлена фізичними властивостями середовища (дисперсійне середовище) або геометрією області, в якій формується хвильове поле (наприклад, хвилевід). В цьому випадку говорять про геометричну дисперсію. Причиною виникнення геометричної дисперсії є та обставина, що хвилеве поле в обмеженій області формується за рахунок багаторазового відбиття хвиль від границі. Саме наявність дисперсії під час поширення хвиль різних частот зумовлює відсутність розв'язку основного рівняння в формі Даламбера. Розповсюдження в середовищі гармонічних хвиль із різними значеннями фазових швидкостей ставить питання про швидкість переносу енергії хвилями в такому середовищі. Першим кроком до формування відповіді на це питання є дослідження хвильового руху, що формується суперпозицією двох гармонічних рухів із різними частотами в дисперсійному середовищі. Для одномірного випадку такий рух можемо представити у вигляді:
.
Для простоти розглядаємо випадок, коли амплітуди гармонічних хвиль однакові. Це суто математичне перетворення дає можливість розглядати суперпозицію двох хвиль, як хвильовий рух із високою (сумарною) частотою, модульований низькочастотним (з різницевою частотою) хвильовим рухом. На рисунку показана анімація такого складного руху.

Видно, що в збуренні формується ряд періодично повторюваних груп, що поширюються зі швидкістю . Якщо спрямувати різницю хвильових чисел в цьому виразі до нуля, приходимо до класичного кінематичного визначення групової швидкості дисперсійних хвиль:
.
Враховуючи дисперсійне співвідношення для згинних хвиль у стрижні , знаходимо . Тобто, групова швидкість згинних хвиль у пружному стрижні вдвічі перевищує фазову швидкість, і більше того, необмежено зростає зі збільшенням частоти. Цей «нефізичний» висновок зумовлений з тим, що рівняння для хвиль у стрижні було виведено з використанням припущень про малість характерного розміру поперечного перерізу стрижня порівняно з довжиною хвилі. У межах такого припущення введено гіпотезу про лінійний розподіл нормальних напружень у поперечному перерізі стрижня. Тому зазначене рівняння непридатне для фізичного аналізу високочастотних збурень, для яких розподіл нормальних напружень у перерізі стрижня має досить складний характер і залежить від частоти. Зі збільшенням частоти довжина хвилі зменшується і може бути значно меншою характерного розміру поперечного перерізу стрижня. У цьому випадку для аналізу дисперсійних властивостей згинних хвиль слід застосовувати повні рівняння динамічної торії пружності.
.

Для ілюстрації впливу дисперсії на розповсюдження збурень на малюнку показано хвильову картину в струні та стрижні для трьох моментів часу. Видно, як руйнується початкова форма збурення за наявності дисперсії. Характер дисперсії такий, що короткі хвилі випереджають довгі[8]
Можна помітити одну суперечність у викладі. Анімація для ілюстрації поняття групової швидкості показує, що групова швидкість менша за фазову, що суперечить зробленому вище висновку. Справа в тому, що наведена анімація відповідає іншому дисперсійному співвідношенню, характерному для хвиль на поверхні води наведена тут лиш для унаочнення суперпозиції гармонічних хвиль. Характер дисперсії хвиль на воді такий, що на відміну від вказаного випадку згинних хвиль у стрижні, першими до спостерігача будуть приходити довгі хвилі (нормальна дисперсія).
Глибше розуміння поняття групової швидкості можна одержати, розглянувши так зване енергетичне визначення цього поняття [11].

Для складніших хвиль у пружних тілах кінематичне та енергетичне визначення групової швидкості наведено в книзі [11]. Доведено, що величини групової швидкості, визначені за кінематичним та енергетичним підходом, збігаються. Саме в пружних хвилеводах можна зустрітися з такими специфічними хвилями, в яких фазова та групова швидкості мають протилежні напрямки [11]. Характер руху в такого типу хвилях показано на анімаційному малюнку.
Характер руху частинок в пружних хвилеводах, що визначається взаємодією поздовжніх та попречних хвиль, дуже складний. Для нормальних хвиль може виникати така ситуація, коли локальні потоки енергії в поперечному перерізі хвилевода для біжучої хвилі мають протилежні знаки. При певних значеннях частоти для другої симетричної хвилі Лемба пружного хвилевода виникає така ситуація, коли біжуча хвиля зі скінченною фазовою швидкістю не переносить енергію (групова швидкість дорівнює нулю).
Взаємодія хвиль із перешкодами[ред. | ред. код]
Характер руху частинок середовища та напрям поширення хвилі може змінюватися за наявності у середовищі неоднорідностей або при падінні хвилі на перешкоди з різними фізичними властивостями. При цьому виникають різні хвильові явища, що вивчаються в теорії хвиль.
Відбиття хвиль[ред. | ред. код]
При розгляді хвильових збурень у нескінченній струні встановлено, що задані збурення одного напрямку (знаку) (всі точки струни зсунуто або вгору, або вниз) при розповсюдженні не переходять через положення рівноваги. Цей факт фізично пояснюється специфікою співвідношення напрямку руху частинок струни (вертикально) та напрямку сили попереднього натягу (горизонтально). Однак у реальних скінченних струнах спостерігається перехід точок через положення рівноваги. Така поведінка скінченної струни визначається особливістю поведінки хвиль при відбитті від точок закріплення. На наведеному малюнку особливість цього процесу відбиття чітко виражена. Ми бачимо «переворот» хвилі при відбиття з повним збереженням форми збурення.

Така проста ситуація не завжди має місце. Процес відбиття хвилі від закріплення може приводити до виникнення нових хвиль і суттєвої зміни форми збурення. Як приклад, розглянемо відбиття згинної хвилі в пружному стрижні від закріпленого кінця. Перш за все треба визначитися з тим, як умови закріплення відображаються в термінах функції , що описує відхилення точок осі стрижня від положення рівноваги. Фізично зрозуміло, що на відміну від струни, закріплення срижня в певній точці можна здійснити двома способами. Можна закріпити точку на осі стрижня, але дозволити вільно повертатися його поперечному перерізу. Таке закріплення називають шарнірним. У термінах функції такі фізичні умови виражаються співвідношеннями . Якщо в другому випадку закріплення здійснити так, щоб заборонялись як зміщення точки на осі стрижня, так і поворот поперечного перерізу (жорстке закріплення) то одержуємо такі граничні умови . Якщо на рух кінця стрижня не накладено кінематичних обмежень і не прикладено механічних сил говорять про вільний кінець. В цьому випадку на кінці стрижня мають виконуватися нульові умови для другої та третьої похідної від функції прогину.
Розглянемо таку ситуацію, коли гармонічна згинна хвиля в напівнескінченному стрижні приходить із нескінченності до точки закріплення з координатою . З урахуванням напрямку розповсюдження функція, що описує відхилення точок осі стрижня від положення рівноваги має вигляд . Для першого (шарнірного) випадку закріплення кінця стрижня відбита хвиля знаходиться досить просто і має вигляд . Обидві граничні умови очевидно виконані для функції . Це сумарне збурення легко представити в явному вигляді . На відміну від біжучих хвиль в одержаному збуренні є точки на осі стрижня , що не відхиляються від положення рівноваги. Такі специфічні типи збурень називають стоячими хвилями. Такі хвилі формуються при суперпозиції двох гармонічних хвиль з однаковими амплітудами, що біжать назустріч одна одній. Характер руху в такій хвилі показано в анімаційному малюнку. Непорушні (вузлові) точки на малюнку позначено червоним.

Принципово відмінна ситуація виникає при аналізі процесу відбиття згинної хвилі в другому випадку граничних умов (жорстке закріплення). Перш за все з'ясовується, що виконати дві граничні умови лише з використанням відбитої біжучої хвилі неможливо. Слід застосувати додатково експоненційно зростаючі та спадаючі складові загального розв'язку (6). Для запобігання громіздких виразів для якісного аналізу ситуації застосовують комплексне представлення розв'язку (6). Падаючу хвилю подають у вигляді . Відбите від жорстко закріпленого кінця поле будується у вигляді . Шуканий розв'язок, що відповідає умовам жорсткого закріплення, подається у вигляді:
.
Таке складне перетворення виконано лише для того, щоб найпростішим шляхом показати механізм формування та характер нового типу гармонічних хвиль — неоднорідних гармонічних хвиль. Це друга складова в наведеному виразі. Для них характерна локалізація збурення поблизу границі з експоненціальним спаданням величини збурень в область існування хвиль. Такі хвилі виникають при розгляді широкого кола задач хвильової динаміки [11].
Дифракція хвиль[ред. | ред. код]
Дифракція — хвильове явище, що спостерігається при взаємодії з перешкодами всіх типів хвиль — звукових, електромагнітних, хвиль на воді. Явище дифракції проявляється особливо помітно, коли розміри перешкоди сумірні з характерною довжиною хвилі збурення. Важливим фактором, що визначає особливості дифракційного поля, є форма перешкоди. Наявність на поверхні перешкоди гострих кутів призводить до значного зростання розсіяння хвиль.
Ефекти дифракції часто проявляються в повсякденному житті. Можливість чути звук від невидимого джерела, блакитний колір неба вдень та рожевий вранці та ввечері — все це зумовлено явищем дифракції. Залежність ефективності дифракційних процесів від довжини хвилі чітко виражена в лісі. Великий розмір листя та частин дерев порівняно з довжиною світлових хвиль не дозволяє бачити далеко. В той же час можливість далеко чути зумовлена відносною малістю вказаних перешкод по відношенню до довжин звукових хвиль чутного діапазону.
Заломлення (рефракція) хвиль[ред. | ред. код]
Якщо перешкодою на шляху хвилі є інше середовище, в якому можуть розповсюджуватися хвилі, частина хвильової енергії падаючої хвилі відбивається, а частина — потрапляє в перешкоду у вигляді хвиль, що можуть у ній поширюватися. Формується досить складна хвильова картина. Певні риси такої хвильової картини можна уявити, розглядаючи модельну задачу відбиття плоскої хвилі від площини, що розділяє два середовища.
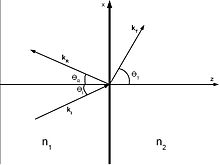
На рисунку представлено схему процесу відбиття хвилі та генерації хвилі, що розповсюджується в лівій півплощині, та генерації хвилі в лівій півплощині. Основним висновком із цього зображення є те, що при проходженні хвилі в середовище з іншими фізичними властивостями змінюється напрям поширення хвилі. Якщо кут падіння хвилі дорівнює куту відбиття у відповідності до закону Снеліуса, то кут, що визначає напрям поширення хвилі, що пройшла в інше середовище не дорівнює куту падіння . Таке явище зміни напрямку поширення хвилі при проходженні із одного середовища в інше, або при поширенні її в середовищі зі змінними в просторі фізичними характеристиками називають заломленням (рефракцією). При великих кутах падіння в правій півплощині вже не може виникати біжуча хвиля. Збурення в ній може існувати лише в формі згаданих неоднорідних хвиль, амплітуда яких швидко спадає з віддаленням від межі. Енергія падаючої хвилі повністю переноситься відбитою хвилею. Таке явище називають явищем повного внутрішнього відбиття хвилі.
Плоскі хвилі[ред. | ред. код]
При розгляді одновимірного хвильового рівняння наведено його загальний розв'язок у формі Даламбера (4). Подібний за фізичною суттю розв'язок існує й для загального тривимірного хвильового рівняння (3). Розглянемо тривимірний простір, положення точок якого задаються декартовими координатами, , з відповідними одиничними векторами . Визначимо в ньому певний напрямок одиничним вектором , так що . Тоді легко перевірити, що вирази
-
()
є розв'язками загального хвильового рівняння (3). Оскільки співвідношенням , де величина деяка стала, визначається площина в просторі, перпендикулярна вектору , то всі точки цієї площини перебувають в однаковій фазі збурення при розповсюдженні хвиль (7). Такі хвилі називаються плоскими. На відміну від одновимірного випадку сума двох хвиль (7) не є загальним розв'язком тривимірного хвильового рівняння. При розповсюдженні і взаємодії з перешкодами дво- і тривимірних хвиль крім біжучих хвиль генеруються неоднорідні хвилі. У частинному випадку гармонічної хвилі загальне представлення для характеристик плоских хвиль використовують в вигляді
-
()
Тут є хвильове число, а компоненти одиничного вектора, що визначає напрям поширення хвилі. Такі гармонічні хвилі з фіксованою частотою називають монохроматичними плоскими хвилями. Моделі плоских хвиль широко застосовуються в задачах акустики та електродинаміки при вивченні процесів розсіювання хвиль різними перешкодами.
Електромагнітні хвилі[ред. | ред. код]
На відміну від механічних хвиль, в яких розповсюдження збурень пов'язане з рухом матеріальних частинок, електромагнітні хвилі, що генеруються під час руху електричних зарядів, можуть поширюватися у вакуумі. Залежно від діапазону частот розрізняють різні типи хвиль, такі як світлові хвилі, радіохвилі, рентгенівське випромінювання та ін.

Ці хвилі можуть розповсюджуватися також у різних матеріальних середовищах. При цьому швидкість хвиль залежить від їх фізичних властивостей. Швидкість електромагнітних хвиль у вакуумі є постійною, незалежною від руху джерела, і її часто називають швидкістю світла.
За сучасними даними швидкість світла в вакуумі дорівнює м/с. На наведеному малюнку показано характер зміни електричної та магнітної компоненти гармонічної плоскої електромагнітної хвилі.
За винятком вказаної здатності розповсюдження у вакуумі, електромагнітні хвилі мають такі ж властивості, як і механічні хвилі.
Гравітаційні хвилі[ред. | ред. код]
Цей тип хвиль було передбачено Ейнштейном в рамках розвиненої ним загальної теорії відносності в 1916 році. Такі хвилі є пульсаціями кривини простору, що поширюються зі швидкістю світла. Джерелом гравітаційних хвиль є будь-яке тіло, що має масу і рухається прискорено. Однак для генерації хвиль з амплітудами, що можуть бути зареєстрованими в земних умовах маси рухомих об'єктів та їх прискорення мають бути дуже великими. Тому як потенційні джерела гравітаційних хвиль розглядаються подвійні зірки та взаємодіючі масивні чорні діри. Вперше в історії гравітаційні хвилі зареєстровані 14 вересня 2015 року двома спеціальними детекторами в США. Зареєстрований сигнал був породжений колапсом двох чорних дір з масами в 36 і 29 сонячних мас. Подія відбулася на відстані 1.3 мільярда світлових років.
Нелінійні ефекти при поширенні хвиль[ред. | ред. код]
Описані вище властивості хвиль одержані на основі математичних моделей, що призводять до лінійних рівнянь. Як правило, такі моделі будуються на основі припущення про відносну малість збурень відповідно до визначального масштабу процесу. Характер таких припущень показано вище при аналізі рівняння руху струни. Однак, у багатьох випадках такі припущення не відповідають справжньому характеру збурень і для опису їх поширення слід застосовувати математичні моделі з нелінійними співвідношеннями. Нелінійні ефекти якісно змінюють поведінку хвилі. Приклад таких змін подано у вступній частині статті при опису стоксового дрейфу частинок рідини при поширенні гравітаційних поверхневих хвиль.
У загальному випадку розрізняють фізичну та геометричну нелінійність. Геометрична нелінійність виникає, наприклад, при аналізі хвиль в струні при відхиленнях точок струні від положення рівноваги сумірних із довжиною хвилі. Джерелом нелінійності можуть бути також фізичні властивості середовища, наприклад, нелінійна залежність відновлюючої сили від деформації в пружному тілі. У цьому випадку кажуть про фізичну нелінійність. Процеси нелінійного деформування вивчаються методами нелінійної механіки. Наявність нелінійності кардинально змінює властивості хвильових процесів. Перш за все перестає бути справедливим принцип суперпозиції. Сума двох розв'язків нелінійного рівняння вже не буде його розв'язком. Важливими стають процеси взаємодії між хвилями (окремими розв'язками рівнянь). Саме нелінійні ефекти зумовлюють можливість існування поодиноких гравітаційних хвиль на мілкій воді — солітонів. Пошуки механізмів виникнення так званих хвиль-убивць, що зустрічаються в різних районах світового океану, значною мірою пов'язані з врахуванням нелінійних ефектів взаємодії гравітаційних хвиль. Перелік і аналіз багатьох нелінійних ефектів наведено в збірнику доповідей конференції, яка в значній мірі вплинула на широкий розвиток досліджень нелінійних хвильових процесів[12]. Дослідження нелінійних ефектів у хвильових рухах інтенсивно проводяться практично в усіх розділах сучасної фізики, механіки, біології[13] 2013 року за цикл робіт «Нелінійні хвилі та солітони у фізиці конденсованого середовища» групі українських вчених присуджено Державну премію України в галузі науки й техніки[14].
Галерея[ред. | ред. код]
Хвильові рухи — це надзвичайно цікаве явище природи.
-
Хвилі на мілководді в басейні. Добре видно відбиті від стінок хвилі та формування складної інтерференційної картини.
-
Набігання хвиль на берег. Нелінійні ефекти на мілкій воді призводять до суттєвої зміни характеру руху частинок рідини та, врешті-решт, до руйнування хвилі.
-
Генерація поверхневої хвилі при падінні краплі на поверхню води. Можна бачити зміну форми хвилі при зростанні відстані до центру збурення, викликану впливом дисперсії. При формуванні та поширенні хвильового збурення таким способом важливу роль відіграють капілярні та гравітаційні сили.
-
Хвилі висотою понад 20 метрів, що утворюються біля одного з Гавайських островів. Мають характерну назву "Щелепи" (Waves "Jaws").
-
Сміливе використання океанічних хвиль.
-
Хвилі Дніпро-Бузького лиману.
-
Хвиляста поверхня Марса, як підстава для тверджень про існування в минулому на планеті води.
-
Рух частинок води в поверхневій хвилі на глибокій воді при використанні лінійного наближення до опису хвильового руху. Траєкторії частинок замкнуті.
-
Рух частинок у хвилі на мілкій воді. Траєкторії частинок води ілюструють пров дрейфу Стокса, зумовленого впливом нелінійності процесу поширення хвиль.
-
Результат чисельного моделювання процесу генерації гравітаційних хвиль при злитті двох чорних дірок. Гравітаційні хвилі вперше зафіксовані на Землі в 2015 році.
-
Ілюстрація пакета амплітудно-модульованої хвилі (червона крива з малою швидкістю).
Швидкозмінна блакитна крива є несучою хвилею, яка модулюється
Див. також[ред. | ред. код]
- Метод стаціонарної фази
- Монохроматична плоска хвиля
- Стояча хвиля
- Дискусія про струну
- Хвилі на поверхні води
- Хвильове рівняння
- Поперечні хвилі
- Поздовжні хвилі
- Коливальна швидкість
- Хвильове число
- Дисперсія хвилі
- Звук
- Акустика
- хвильовий опір
- Хвилі-вбивці
- Хвилі Лемба
Примітки[ред. | ред. код]
- ↑ Зоммерфельд А. Механика деформируемых сред. — М.: Издательство иностранной литературы,1954. — 488 с.
- ↑ Алмазов Л., Кикоин И. Что такое волна? // Квант, 1982, № 6, С. 2-7
- ↑ Longitudinal and Transverse Wave Motion (англ.). Архів оригіналу за 14 січня 2015. Процитовано 17 листопада 2014.
- ↑ Waves: Light, Sound, and the nature of Reality. YouTube. Physics Videos by Eugene Khutoryansky. 3 травня 2015. Процитовано 9 червня 2021.
{{cite web}}: Обслуговування CS1: Сторінки з параметром url-status, але без параметра archive-url (посилання) - ↑ Кадомцев Б. Б.,Рындик В. И. Волны вокруг нас. — М.: Знание,1981. — 152 с.
- ↑ Ламб Г. Гидродинамика. — М.:- Л.: Издательство технико-теоретической литературы, 1947, — 928 с.
- ↑ Myrhaug D., Wang H., Hormedal L. S. Stokes drift estimation for deep water waves based on short-term variation of wave conditions // Costal Engineering, 2014, vol.88, P. 27-32.
- ↑ а б в г д е ж Грінченко В. Т., Вовк І. В., Маципура І. Т. Основи акустики [Архівовано 9 березня 2016 у Wayback Machine.], Київ.: Наукова думка, 2007, — 640 с.
- ↑ Перестюк М. О., Маринець В. В. Теорія рівнянь математичної фізики: Навчальний посібник. — К.: Либідь,2001. — 336 с.
- ↑ Лайтхил Дж. Волны в жидкости. — М.: Мир, 1981. — 598 с.
- ↑ а б в г В. Т. Грінченко,В. В. Мелешко Гармонические колебания и волны в упругих телах. — К.: Наукова думка, 1981. — 281 с.
- ↑ Нелинейная теория распространения волн / Под ред. Г. И. Баренблата. — М.: Мир, 1970. − 231 с.
- ↑ Анісімов І. О. Коливання та хвилі. Навч. посібник. — К.: Академпрес, 2003. — 280 с. — ISBN 966-7541-25-8.
- ↑ Указ Президента України «Про присудження Державних премій України в галузі науки і техніки 2013 року» від 23.08.2014 № 675/2014
Література[ред. | ред. код]
- Коливання та хвилі: підруч. для студ. вищ. навч. закл. / І. О. Анісімов ; М-во освіти і науки України, Київ. нац. ун-т ім. Т. Шевченка. — 2-ге вид., переробл. і доповн. — К. : ВПЦ «Київ. ун-т», 2009. — 399 с. : іл. — Бібліогр.: с. 384 (11 назв). — ISBN 978-966-439-177-8
- Кучерук І. М., Горбачук І. Т., Луцик П. П. Загальний курс фізики: Навчальний посібник у 3-х т, т.1. — К.: Техніка, 1999, — 536 с. — ISBN 966-575-017-8.
- Грінченко В. Т., Вовк І. В., Маципура В. Т. Основи акустики: Навчальний посібник [Архівовано 9 березня 2016 у Wayback Machine.]. — К.: Наукова думка, 2007. — 640 с. — ISBN 978-966-00-0622-5.
- Гринченко В. Т., Мелешко В. В. Гармонические колебания и волны в упругих телах. — К.: Наукова думка, 1981. — 284 с.
- Вакуленко М. О. Тлумачний словник із фізики / М. О. Вакуленко, О. В. Вакуленко. — К. : Видавничо-поліграфічний центр «Київський університет», 2008. — 767 с.
- Поширення хвиль у пружних середовищах з урахуванням зв'язності фізико-механічних полів / Ю. О. Пир'єв; Львів. держ. ун-т ім. І.Франка. — Л. : Світ, 1998. — 203 c. — Бібліогр.: 230 назв.
- Красильников В. А. Звуковые волны в воздухе, воде и твердых телах. — М.:: Гостехиздат, 1954. — 440 с.
| |||||||||||||||||||||||














![{\displaystyle \left[{\frac {\partial w}{\partial x}}\right]^{2}\ll 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/581c59b92819459956dcbe4a0ec4464cfb8675c4)