Джиріх

Матеріал з Вікіпедії — вільної енциклопедії.
Перейти до навігації Перейти до пошуку
Складний орнамент джиріх з 16-, 10- та 8-кутними зорями на різних рівнях на стелі мавзолею Гафіза у Ширазі, 1935

Джиріх (перс. گره‎, джиріх, буквально — «вузол»), також джиріх сазі (перс. گره سازی‎, «плетіння вузлів») або джиріх чіні (перс. گره چینی‎), — це форма ісламського декоративного мистецтва, яка використовується в архітектурі та народних ремеслах (обкладинках книг, шпалерах, маленьких металевих предметах) і складається з геометричних ліній, які формують переплетений орнамент. В іранській архітектурі, орнаменти джиріх сазі можна побачити у цегляних орнаментах баннаї, стукко та мозаїчному фаянсі.[1] Джиріх визначається як «геометричні (часто з зір та багатогранників) орнаменти, які складаються або генерується з масивів точок, з яких лінії побудови виходять та в яких вони перетинаються.»[2]

Для джиріх використовуються симетричні форми з прямими сторонами; типово він складається з плетеного орнаменту, який формує 6-, 8-, 10- або 12-вершинні зорі розділені багатогранниками та смугами, та часто намальованим з перетином. Такі орнаменти зазвичай складаються з повторюваних «одиничних елементів» з 2-, 3- або 6-кратною обертальною симетрією, які ділять площину без дір[3].

Тривимірним еквівалентом джиріх вважаються мукарни[4], які використовуються для декорування нижньої сторони куполів або тромпів.

Історія

[ред. | ред. код]
Мозаїка з давньоримського театру (2 ст. н. е.) у Босрі (Сирія) демонструє криволінійні вузлові орнаменти, які могли бути предком орнаментів джиріх.

Вважається, що витоком орнаментів джиріх є давньоримські вузлові орнаменти давньоримської провінції Сирія, що датуються 2-м ст. н. е.[1], криволінійні переплетені лінії з трикратною обертальною симетрією. У Великій мечеті (709—715), Дамаск, Сирія, є віконні екрани, створені з переплетених хвилястих ліній, які формують шестикутні зорі[5]. Віконні решітки у палаці Гішама поблизу Єрихона  (бл. 730 р.) також виконані зі сплетінням, однак з вигнутих ліній.[6] Вигнутий вузловий орнамент присутній і на різьбленій штукатурці головної мечеті міста Наін, Іран (бл. 960 р.)[7]. Одні з найраніших архітектурних прикладів геометричних орнаментів з прямих переплетених ліній можна побачити на порталі мавзолею Араб Ата (10-те ст.), селище Тім поблизу Самарканд, Узбекистан[8] та на Рибат-і-Махі, Іран (1019—1020)[9].

Ілюмінування

[ред. | ред. код]
Ілюмінація у манускрипті Корану (391 AH, 1000—1001 рр.), виконана Ібн-аль-Баввабом

Найраніше відоме використання джиріх у книзі — фронтиспіс  манускрипту Корані 1000 р.н. е., знайденому у Багдадіі[10]. У цьому Корані є ілюмінована сторінка з переплетеними восьмикутниками та каліграфією сулюс[11].

Роботи по дереву

[ред. | ред. код]
Сторона мінбару (збудований у 13-му ст.) у мечеті Ібн-Тулуна.

Один з найбільш ранніх прикладів використання ісламського геометричного мистецтва у дереві — мінбар 13-го ст. у мечеті Ібн-Тулуна в Каїрі.[12]

У роботах по дереву орнаменти джиріх можливо створити одним з двох методів. В одному, спочатку створюється дерев'яна решітка з геометричними формами (багатогранниками та зорями); після чого прорізи решітки або лишаються пустими, або заповнюються іншими матеріалами. В другому методі, який має назву  джиріх чіні[13] спочатку створюються дерев'яні панелі («плитка») геометричних форм, які потім поєднуються для створення складного малюнка.[1] Цей метод був популярний за династії Сефевідів, а його приклади можна побачити в історичних будівлях Ісфахану.

Архітектура

[ред. | ред. код]
Орнамент джиріх на стінах довкола порталу у медресе Хунат Хатун (архітектура Сельджуків — бл. 1178—1243) у Кайсері, Туреччина.

Турецькою термін «джиріх» використовувався для позначення стрічкового орнаменту з багатогранників в архітектурі ще з кінця 15-го ст.[14] У той же час орнаменти джиріх були зібрані ремісниками у каталоги орнаментів, напр. сувій Топкапи.[15]

Хоча криволінійні попередники джиріх були відомі у 10-му ст., повністю розвинені орнаменти джиріх з'явилися в 11-му ст. в Ірані та стали домінівним елементом дизайну в 11-12-му ст. (наприклад, панелі різьбленого стукко з переплетеним джиріх у вежах Харракан (1067 та 1093) поблизу Казвіна, Іран.[1][16] Деколи з джиріх координували декор зі стилізованих квіток.[17]

Після періоду Сефевідів, використання джиріх продовжувалось у періоді панування Сельджуків та Хулагуїдів. У 14-му ст. джиріх став незначним елементом декоративних мистецтв та був фактично замінений рослинними орнаментами у еру Тімурідів. Однак у центральноазійських монументах орнаменти з геометричних стрічок лишались вадливим елементом декоративного мистецтва і після Тимурідів.[1]

Створення

[ред. | ред. код]
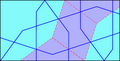
Орнамент джиріх, який можна створити за допомогою циркуля та лінійки
Віконна решітка у палаці Топкапи, яка використовує орнамент зліва.

Перші орнаменти джиріх були утворені шляхом копіювання зразка орнаменту вздовж регулярної решітки; орнамент малювали за допомогою циркуля та лінійки. Сьогодні митці, які працюють у традиційній техніці, переважно використовують пару штангенінструменти, щоб отримати насічку на листі паперу, який залишили на сонці, щоб він став крихким. Прямі лінії малюють за допомогою олівця та немаркованої лінійки.[13] Зроблені таким чином орнаменти джиріх схожі на двовимірний кристал, поділяючи площину одиничним елементом. Оскільки поділ здійснювався за допомогою операцій перекладу чи обертання, одиничні елементи мали  2-, 3-, 4- чи 6-кратну обертальну симетрію.[18]

Плитка джиріх

[ред. | ред. код]
Докладніше: Джиріх (математика)

Десь з 1200 року орнаменти джиріх почали робити з орнаментів у формі зірок та багатокутників, які мали 5- та 10-кратну обертальну симетрію. Такі фігури також можна намалювати за допомогою циркуля та лінійки. Але приблизно з початку 15-го сторіччя деякі орнаменти джиріх уже не були періодичними, такі орнаменти створювались за допомогою плитки джиріх — набору з 5 плиток з намальованими на них лініями; при поділі за їх допомогою площини без дірок, лінії на плитці утворювали орнамент джиріх. Нараз не відомо, коли плитка джиріх була вперше використана замість побудови за допомогою циркуля та лінійки, але вважається ймовірним, що це було у деяких будівлях, створених бл. 1200.[19]

Форми плитки джиріх

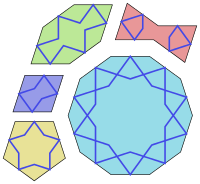
П'ять форм плитки джиріх:

  • правильний десятикутник з 10-ма внутрішніми кутами по 144°;
  • витягнутий (нерегулярно опуклий) шестикутник з внутрішніми кутами 72°, 144°, 144°, 72°, 144°, 144°;
  • метелик (неопуклий шестикутник) з внутрішніми кутами 72°, 72°, 216°, 72°, 72°, 216°;
  • ромб з внутрішніми кутами 72°, 108°, 72°, 108°; та
  • правильний п'ятикутник з 5-ма внутрішніми кутами по 108°.

Всі сторони цих фігур мають однакову довжину, а всі їх кути є множниками 36° (π/5 радіанів). Всі вони, крім п'ятикутника, мають двосторонню (дзеркальну) симетрію відносно двох перпендикулярних ліній. Деякі мають додаткові симетрії: наприклад десятикутник має десятикратну обертальну симетрію (обертання на 36°), а п'ятикутник має 5-кратну обертальну симетрію (обертання на 72°).

  • Орнамент джиріх, виконаний з плитки джиріх.
    Орнамент джиріх, виконаний з плитки джиріх.
  • Деталь з мечеті Єсил (Бурса, Туреччина), виконана орнаментом джиріх зліва.
    Деталь з мечеті Єсил (Бурса, Туреччина), виконана орнаментом джиріх зліва.

Дворівневий дизайн

[ред. | ред. код]
  • Орнамент джиріх на антревольті святилища Дарб-е-Імам, Ісфахан
    Орнамент джиріх на антревольті святилища Дарб-е-Імам, Ісфахан
  • Реконструкція більш масштабного орнаменту з більшою плиткою джиріх. Контур антревольта показаний жовтою пунктирною лінією
    Реконструкція більш масштабного орнаменту з більшою плиткою джиріх. Контур антревольта показаний жовтою пунктирною лінією
  • Правило поділу, використане для створення орнаменту джиріх на антревольті. Велика плитка у формі десятикутника та метелика поділена на меншу плитку джиріх. На самому антревольті, декоративні лінії маленької плитки заповнені чорним (згори зліва)
    Правило поділу, використане для створення орнаменту джиріх на антревольті. Велика плитка у формі десятикутника та метелика поділена на меншу плитку джиріх. На самому антревольті, декоративні лінії маленької плитки заповнені чорним (згори зліва)

Орнаменти джиріх на святилищі Дарб-е-Імам, збудованому 1453 року в Ісфахані, мали значно складнішу структуру, ніж бачені до того. Деталі орнаменту вказують, що замість циркуля та лінійки була використана плитка джиріх. Орнамент на цьому здається аперіодичним; зокрема, на площі стіни, яку він займає, він не регулярно не повторюється. Також орнамент джиріх у святилищі Дарб-е-Імам намальованих у двох масштабах: більший орнамент можна побачити, споглядаючи будівлю здалека, а орнамент меншого масштабу, який є частиною більшого, видно, коли стояти поруч з будівлею.

Хоча існують певні свідчення, що в деяких стародавніх орнаментах джиріх використовувалось правило поділу для створення двох рівнів малюнку, на цей час не виявлено історичних прикладів можливості застосування правила поділу нескінченну кількість разів. Наприклад, орнамент антревольта  Дарб-е-Імаму складається лише (див.малюнок) з десятикутників та метеликів, а правило поділу використовує ці два елементи та плитку з видовженого шестикутника. Тому цей орнамент не має самоподібності на рівнях 1 та 2. А поділ площини, який містить дванадцятикутники та має самоподібність на різних рівнях, що виникає під застосування правила поділу декілька разів, утворює квазікристалічний поділ (див. секцію Аперіодичність нижче).

Аперіодичність

[ред. | ред. код]
Див. також: Аперіодична мозаїка

Періодичний поділ площини виникає внаслідок постійного повторення «одиничного елемента» (форми або набору форм, які повторюються) без пропусків. Таким поділ можна розглядати як двовимірний кристал, і з урахуванням теореми кристалографічного обмеження, одиничний елемент обмежений обертальною симетрією 2, 3, 4 та 6 кратності. Тому площину неможливо періодично поділити фігурами, які мають 5-кратну обертальну симетрію, наприклад 5-кутною зіркою чи десятикутником. Форми з 5-кратною симетрією повторюються на площині періодично, але простір між ними заповнений іншими формами, які не мають періодичності. Такий поділ називається квазі-кристалічним.

Одним зі шляхів створення квазі-періодичного орнаменту є створення мозаїки Пенроуза. Плитка джиріх може бути поділена на мозаїку Пенроуза — форми під назвою «тонкі ромби» («дротики дартс») та «товсті ромби» («повітряні змії»), але не знайдено доказів, що такий підхід використовувався стародавніми майстрами.[19] Іншим шляхом створення квазіперіодичних орнаментів є постійний поділ плиток джиріх на менші плитки джиріх з використанням правила поділу. Обмежена площина таким чином буде поділена на плитки джиріх, які повторюються з аперіодичною частотою. Використання такого правила поділу було б свідченням, що ісламські майстри 15-го ст. розуміли, що плитка джиріх утворює орнаменти, які ніколи точно себе не повторюють. Однак всі відомі орнаменти джиріх містять всього один чи два рівні, та і на практиці у третьому рівні не було потреби, оскільки він був би дуже великим або дуже мілким для споглядання. Тому вважається, що середньовічні ісламські майстри використовували інструмент створення дуже складних орнаментів, але не розуміли цього[20].

Сувій Топкапи

[ред. | ред. код]
Малюнок зі свитку Топкапи. Чорні лінії показують орнамент джиріх, а тонкі червоні лінії — контури плиток джиріх.

Сцвій Топкапи, який датується кінцем 15 ст., є збіркою різних орнаментів та показує, що для створення орнаментів джиріх використовувалась плитка джиріх. Малюнки у свитку показують лінії джиріх поверху контурів плитки, яку використовували для створення орнаменту.[19]

  • Малюнок зі свитку Топкапи з орнаментом джиріх на двох рівнях (масштабах) та плитку джиріх, яка потрібна для його створення.
    Малюнок зі свитку Топкапи з орнаментом джиріх на двох рівнях (масштабах) та плитку джиріх, яка потрібна для його створення.
  • Реконструкція орнаменту маленького масштабу (товсті чорні лінії) з малюнку зліва, з використанням маленької плитки джиріх.
    Реконструкція орнаменту маленького масштабу (товсті чорні лінії) з малюнку зліва, з використанням маленької плитки джиріх.
  • Реконструкція орнаменту великого масштабу (товсті червоні лінії) з малюнку зліва, з використанням великої плитки джиріх.
    Реконструкція орнаменту великого масштабу (товсті червоні лінії) з малюнку зліва, з використанням великої плитки джиріх.

Галерея

[ред. | ред. код]

Див. також

[ред. | ред. код]

Примітки

[ред. | ред. код]
  1. ↑ а б в г д Gereh Sazi. Encyclopaedia Iranica Online. Архів оригіналу за 8 грудня 2015. Процитовано 1 січня 2013.
  2. ↑ Terry Allen (2004). Islamic Art and the Argument from Academic Geometry. Архів оригіналу за 4 липня 2012. Процитовано 23 січня 2012.
  3. ↑ Lee, A.J. Islamic Star Patterns. Muqarnas. 4: 182—197. JSTOR 1523103.
  4. ↑ Rogers, J.M. (1997). Notes on a recent study of the Topkapı scroll: a review article. Bulletin of the School of Oriental and African Studies, University of London. 60 (3): 433—439. doi:10.1017/s0041977x0003247x. JSTOR 619536.
  5. ↑ Umayyad Mosque, Damascus, Syria; Window screen, west vestibule. ArchNet. Процитовано 12 лютого 2012.[недоступне посилання з квітня 2019]
  6. ↑ Khirbat al-Mafjar shiero grill window. Khalili Research Centre. Процитовано 12 лютого 2012.[недоступне посилання з травня 2019]
  7. ↑ Friday Mosque of Na'in, Na'in, Iran. ArchNet. Процитовано 12 лютого 2012.[недоступне посилання з квітня 2019]
  8. ↑ Detail of the Arab Ata Mausoleum portal. ProfiMedia. Архів оригіналу за 13 червня 2021. Процитовано 12 лютого 2012.
  9. ↑ Ribat-i Mahi, Ribat-i Mahi, Iran. ArchNet. Процитовано 12 лютого 2012.[недоступне посилання з квітня 2019]
  10. ↑ Materials and Mediums. Pattern in Islamic Art. Архів оригіналу за 16 лютого 2016. Процитовано 8 лютого 2012.
  11. ↑ The transformation of Islamic art during the Sunni revival. I.B.Tauris. 2002. с. 84. ISBN 978-1-85043-392-7. Архів оригіналу за 1 серпня 2020. Процитовано 12 лютого 2016.
  12. ↑ Jami' Ibn Tulun. Процитовано 22 лютого 2012.[недоступне посилання з квітня 2019]
  13. ↑ а б Richard Henry (2007). Pattern, Cognition and contemplation: Exploring the Geometric Art of Iran (PDF). Iran Society. Архів оригіналу (PDF) за 11 червня 2014. Процитовано 8 лютого 2012.
  14. ↑ Dündar, A. (2003). Bir Belgeye Göre Amasya II. Bayezid Külliyesi (PDF). Ankara Üniverstesi İlahiyat Fakültesi Dergisi (Turkish) . 44 (2): 131—172. Архів оригіналу (PDF) за 3 червня 2018. Процитовано 12 лютого 2016.
  15. ↑ Katz, V.J. (2007). The Mathematics of Egypt, Mesopotamia, China, India, and Islam. Princeton University Press. с. 620. ISBN 978-0-691-11485-9. Архів оригіналу за 30 червня 2014. Процитовано 12 лютого 2016.
  16. ↑ Architecture – iv. Central Asian. Encyclopaedia Iranica. 11 серпня 2011. Архів оригіналу за 4 березня 2016. Процитовано 8 лютого 2012.
  17. ↑ G. A. Pugachenkova, A. H. Dani and Liu Yingsheng (2000). Urban development and architecture. History of Civilizations of Central Asia Volume IV: The Age of Achievement: A.D. 750 to the End of the Fifteenth Century – Part Two: The Achievements. unesco. ISBN 978-92-3-103654-5. Архів оригіналу за 4 березня 2016. Процитовано 12 лютого 2016.
  18. ↑ Cromwell, P.R. (2009). The Search for Quasi-Periodicity in Islamic 5-fold Ornament. Mathematical Intelligencer. 31 (1): 36—56. doi:10.1007/s00283-008-9018-6.[недоступне посилання з листопадаа 2019]
  19. ↑ а б в Peter J. Lu and Paul J. Steinhardt (2007). Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture (PDF). Science. 315 (5815): 1106—1110. Bibcode:2007Sci...315.1106L. doi:10.1126/science.1135491. PMID 17322056. Архів оригіналу (PDF) за 7 жовтня 2009. Процитовано 12 лютого 2016.
  20. ↑ Emil Makovicky. Comment on "Decagonal and Quasi-Crystalline Tilings in Medieval Islamic Architecture". Архів оригіналу за 18 жовтня 2014. Процитовано 22 лютого 2012.

Посилання

[ред. | ред. код]
Вікісховище має мультимедійні дані за темою: Джиріх
Отримано з https://uk.wikipedia.org/w/index.php?title=Джиріх&oldid=43475381