Теселяція


| Ця стаття містить правописні, лексичні, граматичні, стилістичні або інші мовні помилки, які треба виправити. |
| Ця стаття не містить посилань на джерела. (квітень 2022) |
Теселя́ція (від лат. tessella — шматок глини, з якого випікали мозаїку), також паркет, паркетаж — мозаїка, складена з кількох абсолютно однакових форм, які прилягають одна до одної без проміжків і не перекривають одна одну.
Парке́т — замощення площини багатокутниками без пробілів і перекриттів, в якому будь-які два багатокутники мають або спільну сторону, або тільки спільну вершину, або зовсім не мають спільних точок.
Прості геометричні теселяції можуть складатися тільки з трьох фігур: рівнобічних трикутників, квадратів і шестикутників.
Одне з перших вивчень теселяцій було зроблене у 1619 році Йоганном Кеплером, який описав правильні багатокутники на площині.
У 1891 році російський кристалограф Євграф Степанович Федоров довів, що кожна частина такої мозаїки з трансляційною симетрією побудована відповідно до однієї з 17 груп ізометрії. Таким чином, існує всього 17 можливих способів розміщення фігури для того, щоб заповнити ними всю поверхню. Всі вони були використані у гравюрах голландського художника Моріца Ешера.
Термінологія[ред. | ред. код]
Замощення, мозаїки, паркети, розбиття[ред. | ред. код]
Паркети інакше називають «замощенням», «мозаїками» (англ. tessellation, tiling), «розбиттям площини» (англ. partition), «паркетажами». Замощення тривимірного простору і просторів вищих розмірностей часто називають стільниками.
Паркети з областями (плитками) довільної форми іноді називають «картами».
Покриття та упаковки[ред. | ред. код]
Якщо об'єднання кількох фігур містить дану фігуру Ф, то кажуть, що ці фігури утворюють покриття фігури Ф. При цьому фігури, які покривають, можуть перекриватися, але вони покривають фігуру Ф без пробілів.
Упаковка — це розміщення всередині даної фігури декількох фігур, які не мають спільних точок, крім, можливо, граничних (тобто без перекриття).
Замощення — це розбиття фігури на частини. Замощення є одночасно покриттям і упаковкою.
Протоплитки[ред. | ред. код]
Протоплитки паркету (англ. prototiles, також прототипи) — це плитки (форми), що входять в паркет. Кожна плитка паркету конгруентна однією з протоплиток.
Так, єдина протоплитка п'ятикутного паркету — правильний шестикутник; протоплиткою правильного сферичного п'ятикутного паркету є пентагон; множина протоплиток ромботришестикутного паркету складається з рівностороннього трикутника, квадрата і шестикутника.
Паркет називається k-едричним, якщо множина його протоплиток (протомножина) складається з k плиток.
Плитки паркету також називають гранями, а сторони багатокутних плиток — ребрами, за аналогією з термінологією для багатогранників.
Конфігурація вершин і граней[ред. | ред. код]
Ромботришестикутний паркет складається з плиток трьох типів: рівносторонній трикутник, квадрат і шестикутник. Ці плитки розташовуються навколо кожної з вершин в такому порядку: трикутник, квадрат, шестикутник, квадрат. Такий порядок називається конфігурацією вершини паркету і записується в формі 3.4.6.4. У разі, якщо два і більше числа в цій послідовності йдуть підряд, використовується скорочений запис. При цьому записи, що відрізняються лише циклічною перестановкою чисел або зміною порядку запису на протилежний (наприклад, 3.3.4.3.4 і 4.3.3.4.3), позначають одну і ту ж конфігурацію вершини; в той же час запис 3.4.4.6 не є еквівалентним запису 3.4.6.4. У неоднорідних паркетах можуть зустрічатися вершини з різними конфігураціями.
Конфігурацією граней називається послідовність степенів вершин цієї межі при обході її в одному напрямку. Конфігурація граней записується послідовністю чисел в квадратних дужках або з префіксом V.
Якщо усі вершини деякого паркету мають одну і ту ж конфігурацію, то всі грані [ [Двоїстий багатогранник | двоїстого]] йому паркету мають одну і ту ж конфігурацію. Наприклад, конфігурації граней паркету, двоїстого ромботришестикутному паркету 3.4.6.4, записуються як V3.4.6.4.
Види паркету[ред. | ред. код]
У багатьох випадках застосовується умова еквівалентності кожної з протоплиток паркету топологічному диску; іншими словами, плитка не повинна складатися з декількох частин (квазіполіміно), містити «отвори», бути нескінченною смугою тощо.
Правильні паркети[ред. | ред. код]
| Вікісховище має мультимедійні дані за темою: Правильні паркети |
Паркети, складені з однакових правильних багатокутників, називають правильними паркетами (англ. regular tilings). Існує три правильних заміщення площини: трикутний паркет, квадратний паркет і шестикутний паркет.
| Правильні паркети | ||||||
|---|---|---|---|---|---|---|
|
Правильні паркети називають також Платоновими паркетами .
Поліформи, що розташовуються на правильних паркетах, називаються відповідно поліамондами, полімін і полігексами.
Для позначення паркету з правильних p — кутників, розташованих по q навколо кожної вершини, застосовується символ Шлефлі { p , q }. Символи Шлефлі трьох правильних мозаїк — {3,6}, {4,4} і {6,3}.
Напівправильні паркети[ред. | ред. код]
Паркети, що складаються з правильних багатокутників двох або більше типів, такі, у яких для всяких двох вершин паркету існує перетворення симетрії (самопоєднання), що переводить одну з них в іншу, називаються напівправильними паркетами, або архімедовим паркетами.
Існує 8 напівправильних паркетів. Один з восьми напівправильних паркетів кирпатий тришестикутний паркет є хіральним, тобто не збігається з власним дзеркальним відображенням.
| Напівправильні паркети (Архімедові паркети) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Однорідні паркети
Існує два визначення, що призводять до одного і того ж набору з 8 напівправильних паркетів на площині.
Перше, «локальне» визначення, полягає в тому, що вершинні конфігурації всіх вершин повинні збігатися. Іншими словами, послідовності граней навколо будь-яких двох вершин паркету повинні бути однаковими: одні і ті ж багатокутники повинні йти в одному і тому ж (або в протилежному) порядку.
Друге, «глобальне» визначення, вимагає, щоб для будь-яких двох вершин паркету існувало перетворення симетрії (самопоєднання паркету), що переводить одну з них в іншу.
Грюнбаум і Шепард поділяють терміни «архімедів паркет» і «однорідний паркет»: до першої групи відносяться паркети, відповідні «локального» визначення, а до другої — «глобального». Хоча на евклідовій площині дві ці множини збігаються, в інших просторах існують архимедові паркети, що не є однорідними.
У математичній літературі значення термінів «архімедів паркет», «напівправильний паркет» і «однорідний паркет» варіруюються.
Квазиправильні паркети[ред. | ред. код]
«Квазіправильний паркет» (або багатогранник) — однорідний паркет (або багатогранник), що складається з граней двох видів, які чергуються навколо кожної вершини; іншими словами, кожна грань оточена гранями іншого типу.
На евклідовій площині існує лише один квазіправильний паркет — тришестикутний паркет з вершинною конфігурацією 3.6.3.6. На сфері існує два квазіправильних паркетів сферичних багатогранника — кубооктаедр і ікосододекаедр.
На площині Лобачевського існує безліч квазіправильних паркетів виду , де .
Неоднорідні паркети[ред. | ред. код]
Існує безліч неоднорідних паркетів, що складаються з правильних багатокутників.
| Неоднорідні паркети з правильних багатокутників | ||||||||
|---|---|---|---|---|---|---|---|---|
|
Періодичні неоднорідні паркети можна класифікувати за кількістю орбіт вершин, ребер і граней. Якщо число орбіт вершин дорівнює «n», паркет називається «n»-однорідним або «n»-ізогональним; якщо число орбіт ребер дорівнює «n» — «n»-ізотоксальним. Вищенаведені приклади являють собою чотири з двадцяти 2-однорідних паркетів.
Неперіодичні паркети і аперіодичні множини плиток[ред. | ред. код]



Розбиття T називається періодичним, якщо серед симетрій «T» існують два паралельні перенесення в непаралельних напрямках. У цьому випадку мозаїку можна вважати складаною з повторень невеликого фрагмента, викладеного із елементів у вузлах деякої решітки. Множина прототипів (протомножин) «P» називається «аперіодичною», якщо вона реалізується в якихось розбиттях площин, але жодне з них не є періодичним.
Перший приклад аперіодичної множини плиток був знайдений Робертом Берджером в 1966 році і включав в себе 20426 плиток Вана. Плитки Вана являють собою квадрати одного розміру з пофарбованими сторонами; при побудові мозаїки дозволено поєднувати плитки лише одноколірними сторонами і заборонено перевертати плитки.
Пізніше були знайдені аперіодичні протомножини з меншим числом плиток. Роджер Пенроуз виявив аперіодичні протомножини, що складаються з двох плиток.
У 2010 році Джошуа Соколар і Джоан Тейлор запропонували аперіодичну множину, що складається з єдиної плитки, яка являє собою правильний шестикутник з нанесеною розміткою у вигляді кольорових ліній і з додатковими обмеженнями, пов'язаними з взаємним розташуванням «'не'» торкаючись один одного. Існує модифікація, яка не використовує подібних обмежень, але використовує незв'язну плитку, тобто, плитку, що не є топологічним диском. Існування єдиної зв'язковий плитки без додаткової розмітки та обмежень, здатної покрити площину тільки аперіодично, залишається відкритою проблемою.
Сферичні багаторанники[ред. | ред. код]
«'Сферичний паркет'» або «'сферичний багатогранник'» — розбиття сфери на сферичні багатокутники, великих кіл.
Кожному з 5 платонових тіл відповідає правильний сферичний паркет. Формально, нехай «S» — сфера з центром «O», що збігається з центром багатогранника «P». Проведені з «O» промені, що проходять через вершини багатогранника «P», перетинають сферу «S» в точках, які є вершинами відповідного сферичного паркету; ребра багатогранника «P» відповідають дугам великих кіл на «S».
Крім сферичних аналогів п'яти «платонових тіл», існує два сімейства правильних сферичних багатогранників, які не мають еквівалентів серед багатогранників з плоскими гранями: осоедри — багатогранники з двома вершинами, які перебувають на полюсах сфери, межі яких є конгруентними двокутниками, і діедри — двоїсті осоедрам двогранники, вершини яких знаходяться на екваторі сфери.

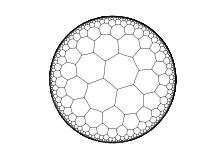
Гіперболічні паркети[ред. | ред. код]
Аксіома паралельності Евкліда (точніше, одне з еквівалентних їй тверджень) свідчить:
|
У геометрії Лобачевського, замість неї приймається така аксіома:
|
Для зображення гіперболічної площини застосовується одна з існуючих моделей — модель Бельтрамі — Кляйна, конформний диск Пуанкаре, модель Пуанкаре на півплощині.
На евклідовій площині існує лише три правильні паркети і 8 напівправильних. На гіперболічній площині існує нескінченна множина навіть правильних паркетів, включаючи паркети з сімома і більше рівносторонніми трикутниками навколо вершини, п'ятьма і більше квадратами, чотирма і більше правильними п'ятикутниками (паркет з трьома п'ятикутниками навколо вершини є сферичним додекаедром), чотирма і більше правильними шестикутниками і трьома і більш рівними правильними багатокутниками з кількістю сторін більше 6.
Задачі на паркеті[ред. | ред. код]
Велика кількість задач і головоломок пов'язані з розбиттям прямокутників (або інших зв'язаних фігур) на плитки з певної заданої множини протоплиток. Самі протоплитки при цьому можуть являти собою зв'язкові об'єднання осередків правильного паркету.
Зокрема, існує клас задач на заміщення прямокутників m × n плитками доміно таким чином, щоб в отриманому розбитті не було прямої лінії, що перетинає прямокутник від краю до краю і не перетинає жодної плитки доміно; такі прямокутники називаються «міцними».
В інших задачах встановлюється додаткове обмеження на кількість плиток кожного виду, які використовуються в замощенні. У задачах, пов'язаних з пентаміно, потрібно покрити 12 фігурами задану підмножину квадратного паркету, що складається з 60 клітин; при цьому кожна плитка повинна бути використана тільки один раз.
Перерахування паркету[ред. | ред. код]
Задача визначення кількості паркетів, що складаються з опуклих багатокутників заданого типу, вирішена лише частково:
- Будь-яким трикутником або чотирикутником можна замістити площину.
- Відомо 15 п'ятикутників, здатних замістити площину; невідомо, чи є цей перелік повним. Проблема перерахування п'ятикутних паркетів має багату історію.
- Відомо 3 типи шестикутників, здатних замістити площину.
- Неможливо замістити площину однаковими опуклими багатокутниками з числом сторін, більшим або рівним семи.
Див. також[ред. | ред. код]
- Стільник (геометрія)
- Діаграма Вороного
- Тріангуляція Делоне
- Мозаїка Пенроуза
- Піфагорова мозаїка
- Проблема чотирьох фарб
- Стереографічна проєкція
- Марджорі Райс
| |||||||||||||||||||||||||
















