Шестикутник

Шестикутник ABCDEF та його діагональ АЕ

В геометрії шестику́тник — планіметрична фігура, многокутник, що має шість сторін, шість вершин та шість кутів.

Також можливе альтернативне визначення:

Шестику́тник — це частина площини, обмежена простою замкнутою ламаною, яка містить шість ланок (має шість кутів). Вона складається з шести точок (вершин шестикутника), послідовно з'єднаних шістьма відрізками (сторони або ребра шестикутника). При цьому жодні три з даних точок не повинні лежати на одній прямій.

Шестикутник позначають, записуючи послідовно його вершини. Наприклад, так: ABCDЕF.

Вершини шестикутника називаються сусідніми, якщо вони є кінцями однієї з його сторін. Відрізки, що сполучають несусідні вершини шестикутника, називаються його діагоналями.

Сторони шестикутника, що виходять з однієї вершини, називаються сусідніми сторонами.

Шестикутник може бути простим (без самоперетинів; може бути опуклим та вгнутим) або схрещеним(з самоперетином). Також існують просторові шестикутники (якщо вищезгадана ламана знаходиться не в площині, а в просторі).

Сума довжин усіх сторін шестикутника називається периметром.

Сума внутрішніх кутів простого шестикутника дорівнює 720°.

$\sum {\alpha =}(n-2)\cdot 180^{\circ }=4\cdot 180^{\circ }=720^{\circ }$

Площа шестикутника без самоперетинів

Площа довільного шестикутника без самоперетинів, що заданий координатами своїх вершин, визначається за формулою площі Гаусса, загальною для багатокутників .

Опуклий шестикутник

Опуклий шестикутник

Опуклим шестикутником називається такий шестикутник, всі точки якого лежать по один бік від будь-якої прямої, що проходить через дві його сусідні вершини.

Можливі також альтернативні визначення.

Опуклим шестикутником називається

— шестикутник, який обмежує опуклу множину. Тобто для будь-яких двох точок шестикутника відрізок, що їх сполучає, повністю належить шестикутнику.

— шестикутник такий, що всі його діагоналі повністю лежать всередині нього.

Внутрішній кут $\alpha$ опуклого шестикутника — кут між двома його сусідніми сторонами. Будь-який внутрішній кут опуклого шестикутника менше 180°.

Сума внутрішніх кутів опуклого шестикутника дорівнює $\sum {\alpha =}(6-2)\cdot 180^{\circ }=4\cdot 180^{\circ }=720^{\circ }=4\pi$ радіан.

Зовнішній кут $\beta$ — кут, що суміжний внутрішньому.

Як і у всіх полігонів, сума зовнішніх кутів (по одному при кожній стороні) становить $360^{\circ }=2\pi$ радіан.

Кількість діагоналей опуклого шестикутника $k={\frac {6\cdot (6-3)}{2}}=9$ (З кожної вершини можна провести 3 діагоналі). Три діагоналі, що сполучають протилежні вершини шестикутника, називають головними діагоналями. Діагоналі, що виходять з однієї вершини, розбивають шестикутник на 4 трикутники.

Серед 17 точок в загальному положенні на площині, серед яких ніякі 3 не лежать на одній прямій, завжди знайдеться 6 точок, які є вершинами опуклого шестикутника. Цей розв'язок задачі зі щасливим кінцем був знайдений за допомогою комп'ютерного перебору можливих конфігурацій.

Конкурентні прямі та колінеарні точки

Конкурентні прямі та колінеарні точки в опуклому шестикутнику

Теорема 1

Нехай А₁А₂А₃А₄А₅А₆ — опуклий шестикутник. Три головні діагоналі в шестикутнику А₁А₄, А₂А₅ і А₃А₆ перетинаються в одній точці, тоді і тільки тоді, коли: ^{:стор.160}

$$\sin \left(\alpha +\alpha ^{+}\right)\cdot \sin \left(\beta +\beta ^{+}\right)\cdot \sin \left(\gamma +\gamma ^{+}\right)\cdot \sin \alpha ^{-}\cdot \sin \beta ^{-}\cdot \sin \gamma ^{-}=\sin \left(\alpha +\alpha ^{-}\right)\cdot \sin \left(\beta +\beta ^{-}\right)\cdot \sin \left(\gamma +\gamma ^{-}\right)\cdot \sin \alpha ^{+}\cdot \sin \beta ^{+}\cdot \sin \gamma ^{+}$$

Теорема 2

Нехай в опуклому шестикутнику А₁А₂А₃А₄А₅А₆ прямі А₁А₂ та А₄А₅ перетинаються в точці K, прямі А₁А₃ та А₄А₆ перетинаються в точці L, a прямі А₂А₃ та А₆А₅ перетинаються в точці M. Тоді, точки K, L, M колінеарні, тобто лежать на одній прямій, тоді і тільки тоді, коли: ^{:стор.165}

$$\sin \left(\alpha +\alpha ^{+}\right)\cdot \sin \left(\beta +\beta ^{+}\right)\cdot \sin \left(\gamma +\gamma ^{+}\right)\cdot \sin \alpha ^{-}\cdot \sin \beta ^{-}\cdot \sin \gamma ^{-}=\sin \left(\alpha +\alpha ^{-}\right)\cdot \sin \left(\beta +\beta ^{-}\right)\cdot \sin \left(\gamma +\gamma ^{-}\right)\cdot \sin \alpha ^{+}\cdot \sin \beta ^{+}\cdot \sin \gamma ^{+}$$

Рівносторонні трикутники на сторонах шестикутника

Рівносторонні трикутники на сторонах довільного шестикутника

Якщо на кожній стороні будь-якого шестикутника зовні побудувати рівносторонній трикутник, то середини відрізків, що з’єднують центроїди протилежних трикутників, утворюють інший рівносторонній трикутник. ^{:Теорема 1}

Шестикутник вписаний в коло

Вписаний в коло шестикутник

Шестикутник називається вписаним в деяке коло, якщо всі його вершини лежать на цьому колі. При цьому коло називається описаним навколо шестикутника.

Центр описаного навколо шестикутника кола лежить на перетині серединних перпендикулярів (або медіатрис) до всіх його сторін.

Аналогічно до вписаного чотирикутника, для вписаного шестикутника справедливі твердження:

1. Суми трьох несусідніх внутрішніх кутів вписаного шестикутника рівні: $\angle A+\angle C+\angle E=\angle B+\angle D+\angle F=360^{\circ }$ .
2. Якщо суми трьох несусідніх внутрішніх кутів опуклого шестикутника дорівнюють 360°, то існує шестикутник з такими ж кутами, навколо якого можна описати коло.

Три діагоналі вписаного шестикутника, що сполучають його протилежні вершини, перетинаються в одній точці якщо: $a\cdot c\cdot e=b\cdot d\cdot f$ ^{:стор.167} .

де a, b, c, d, e, f — довжини послідовних сторін шестикутника.

Нехай p₁, p₂, p₃, p₄, p₅, p₆ — відстані від довільної  точки M описаного кола до сторін AB, BC, CD, DE, EF, AF відповідно. Тоді виконується рівність:

p₁p₃ p₅ = p₂p₄p₆.

Вписаний шестикутник (як і будь-який вписаний багатокутник) можна розбити на рівнобедрені трикутники, вершини яких лежать в центрі описаного кола, а бокові сторони є радіусами кола, що проходять через його вершини.

Шестикутник Лемуана

Шестикутник Лемуана — це вписаний в коло шестикутник, вершини якого є точками перетину сторін трикутника з прямими, що паралельні до його сторін і проходять через його точку Лемуана.

Шестикутник Лемуана з самоперетинами є зіркоподібним, його ядром є лише одна точка.

Теорема Дао

Нехай на сторонах вписаного шестикутника побудовані зовнішнім чином трикутники, шляхом продовження сторін шестикутника до їх взаємного перетину. Тоді відрізки, що з'єднують центри описаних кіл протилежних трикутників перетинаються в одній точці. (Теорема Дао)

Наслідок теореми 1 та 2 про конкурентні прямі опуклого шестикутника:

Нехай вершини цих трикутників , що не належать сторонам вписаного шестикутника позначені як B₁, B₂, B₃, B₄, B₅, B₆ Тоді, головні діагоналі шестикутника B₁B₂B₃B₄B₅B₆ (ті, що з'єднують протилежні вершини, тобто B₁B₄, B₂B₅, B₃B₆ ) перетинаються в одній точці. ^{:стор.167}

Теорема Фурмана для вписаного шестикутника

Теорема Фурмана

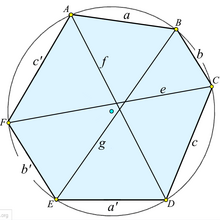
Також її називають теоремою Птолемея для вписаного шестикутника.

Нехай протилежні сторони вписаного шестикутника дорівнюють $a,a'$ , $b,b'$ та $c,c'$. І нехай головні (ті, що сполучають протилежні вершини) діагоналі шестикутника дорівнюють $e$ , $f$ та $g$ (e лежить між сторонами $a$ та $a'$, f лежить між сторонами $b$ та $b'$, g лежить між сторонами $c$ та $c'$). Тоді виконується рівність:

$e\cdot f\cdot g=a\cdot a'\cdot e+b\cdot b'\cdot f+c\cdot c'\cdot g+a\cdot b\cdot c+a'\cdot b'\cdot c'$

Рівність також справедлива, якщо всі шість точок A, B, C, D, E, F лежать на одній прямій.

Якщо шестикутник не є вписаним в коло, то добуток діагоналей буде менше виразу, що стоїть в правій частині.

Теорема Паскаля

Теорема Паскаля

Якщо шестикутник вписано в коло, чи будь-який інший конічний перетин (еліпс, параболу, гіперболу, пару прямих), то точки перетину трьох пар протилежних сторін лежать на одній прямій. Теорема Паскаля двоїста до теореми Бріаншона.

Шестикутник описаний навколо кола

Описаний шестикутник

Шестикутник називається описаним навколо деякого кола, якщо це коло дотикається до всіх сторін шестикутника. При цьому коло називається вписаним в шестикутник.

Центр вписаного в шестикутник кола лежить на перетині бісектрис його внутрішніх кутів. І навпаки, якщо всі бісектриси внутрішніх кутів деякого шестикутника перетинаються в одній точці, то в цей шестикутник можна вписати коло з центром в цій точці.

В шестикутник можна вписати коло радіусом r, якщо виконується рівність:

$a+c+e=b+d+f$

Якщо суми трьох несуміжних сторін дорівнює сумі трьох інших його сторін, то існує шестикутник з такими ж сторонами, в який можна вписати коло.

Діагоналі ,що сполучають протилежні вершини описаного шестикутника, перетинаються в одній точці.

Радіус вписаного кола  : $r={\frac {S}{p}}={\frac {2S}{a+b+c+d+e+f}}$

де S - площа шестикутника, p - півпериметр.

Теорема Бріаншона

Теорема Бріаншона

Якщо шестикутник описано навколо кола, чи будь-якого іншого конічного перетину (еліпса, параболи, гіперболи, пари прямих), то три діагоналі, що з'єднують протилежні вершини цього шестикутника, проходять через одну точку.

Теорема є двоїстою до теореми Паскаля.

Рівносторонні та рівнокутні шестикутники

Приклади рівносторонніх шестикутників

Приклади рівнокутних шестикутників

У рівнокутному шестикутнику кожен кут дорівнює $180^{\circ }-{\tfrac {360^{\circ }}{6}}=120^{\circ }$.

Для рівнокутних шестикутників виконується теорема Вівіані: ^{:стор.2, 11}

Сума відстаней від внутрішньої точки до сторін рівнокутного шестикутника не залежить від розташування точки і є інваріантом багатокутника.

Рівнокутний шестикутник з цілими довжинами сторін можна поділити на правильні трикутники. .

Вписаний шестикутник рівнокутний тоді й лише тоді, коли сторони, що чергуються, рівні . Прикладами можуть бути правильний шестикутник та дітригон.

Описаний шестикутник є рівностороннім в тому і тільки в тому випадку, коли його кути через один рівні. Прикладами можуть бути правильний шестикутник та тріамбус.

Правильний шестикутник є одночасно рівнокутним та рівностороннім.

Кожна головна діагональ шестикутника ділить його на чотирикутники. В будь-якому опуклому рівносторонньому шестикутнику із стороною $a$ існує головна діагональ $d_{1}$, така що:

${\frac {d_{1}}{a}}\leqslant 2$,

і головна діагональ $d_{2}$, така, що:

${\frac {d_{2}}{a}}>{\sqrt {3}}$.

Існує скінченна послідовність елементарних відбиттів, які переводять будь-який рівносторонній шестикутник у правильний.

Замощення площини шестикутними зоногонами.

Опуклий шестикутник, у якого протилежні сторони та кути рівні, є зоногоном. Шестикутні зоногони є паралелогонами, тобто однаковими копіями шестикутних зоногонів можна замостити площину без проміжків та накладень.

Гарольд Коксетер стверджує, що кожен зоногон (2m-кутник, протилежні сторони якого паралельні й мають однакову довжину) можна розрізати на ${\binom {m}{2}}={\frac {m\cdot (m-1)}{2}}$ паралелограмів. . У випадку правильного шестикутника, паралелограми є ромбами.

Розбиття шестикутника на ромби та паралелограми
2D	Ромби	Паралелограми
	Правильний {6}	Шестикутні паралелогони

Правильний шестикутник

Правильний шестикутник

Правильний шестикутник (гексагон) — це правильний багатокутник з шістьма сторонами.

Правильний шестикутник — опуклий шестикутник, у якого всі сторони і кути рівні.

Внутрішній кут правильного шестикутника дорівнює 120°. Центральний кут дорівнює 60°.

Правильний шестикутник є унікальним (в межах подібності) серед шестикутників, оскільки він рівносторонній, і всі його шість кутів рівні між собою. Він є вписаним і описаним одночасно.

Особливість правильного шестикутника — рівність його сторони і радіуса описаного навколо нього кола.

Правильний шестикутник має шість ліній дзеркальної симетрії, і обертову симетрію 6-го порядку (у 60°, 120°, 180°, 240° та 300°). Має центр симетрії.

Правильний шестикутник сторони якого перетинаються (або зірковий шестикутник) називається гексаграмою.

Неопуклі та зірчасті шестикутники

Теорема Паппа

Теорема Паппа

Нехай точки А, В, С лежать на одному боці кута, а точки А₁, В₁, С₁ – на іншому. Якщо прямі АВ₁ та А₁В перетинаються у точці М, АС₁ та А₁С – у точці L, а ВС₁ та В₁С – у точці К, то точки К, L, М лежать на одній прямій.

Теорема Паппа є виродженим випадком в теоремі Паскаля: якщо замінити в теоремі Паскаля вписаний у конічний перетин шестикутник на вписаний у пару прямих, які перетинаються, то вона стане еквівалентною теоремі Паппа.

Шестикутники з самоперетинами

Наступні шість шестикутників з самоперетином мають розташування вершин як у правильному шестикутнику:

Dih2			Dih1		Dih3			Dih6
Вісімко-подібний шестикутник	Схрещений шестикутник	Унікурсальна гексаграма	Шестикутник - риб'ячий хвіст	Шестикутник - одвійний хвіст	Шестикутник - потрійний хвіст	Тріпод	Пропелерний тріпод	Правильна гексаграма 2{3}
					Гіперзрізані трикутники

Схрещений шестикутник	Неопуклий шестикутник	Зірчастий шестикутник

Гексаграма

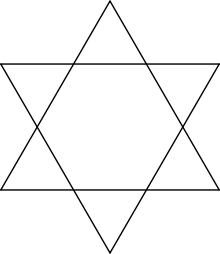
Шестикутник з самоперетинами, що має рівні сторони та кути, а вершини розташовані як вершини правильного шестикутника називається гексаграмою. Гексаграма є єдиною зірчастою формою правильного шестикутника і утворена поєднанням двох протилежно орієнтованих правильних трикутників. Має повну діедральну симетрію D₆ (Dіh₆) правильного шестикутника.

Просторовий шестикутник

Правильний просторовий шестикутник в ребрах та вершинах трикутної антипризми.Симетрія D_3d, [2⁺,6], (2*3), порядок 12.

Просторовий (або косий) шестикутник це просторовий замкнутий багатокутник з шістьма вершинами та шістьма ребрами, що не належать одній площині. Внутрішня частина такого шестикутника не визначена.

Просторовий зигзагоподібний шестикутник має вершини, що чергуються в двох паралельних площинах.

Правильний просторовий шестикутник є багатокутником перті куба

Правильний просторовий шестикутник є вершинно-транзитивним з рівними довжинами ребер. А отже, також є зигзагоподібним. В тілах тривимірного простору косий правильний шестикутник можна побачити в вершинах та ребрах трикутної антипризми з симетрією D_3d, [2⁺,6] , порядок 12. Куб і октаедр (те саме, що трикутна антипризма) мають правильні косі шестикутники як багатокутники Петрі.

Просторовий шестикутник на осях 3-кратної симетрії

Куба

Октаедра

Багатокутники Петрі

Правильний косий шестикутник є багатокутником Петрі для наступних правильних, однорідних та двоїстих багатогранників та політопів в просторах високої розмірності, показаних в косих ортогональних проєкціях:

4D		5D
3-3 дуопризима	3-3 дуопризима	5-симплекс

Замощення площини шестикутними паркетами

Шестикутники з симетріями g2, i4, та r12, як паралелогони, можуть замостити площину власними копіями, отриманими тільки за допомогою паралельного перенесення. Інші форми шестикутних паркетів можуть заміщувати площину в різних орієнтаціях.

p6m (*632)	cmm (2*22)	p2 (2222)	p31m (3*3)	pmg (22*)		pg (××)
r12Паркет з правильних шестикутників	i4	g2	d2	d2	p2	a1
Dih6	Dih2	Z2	Dih1			Z1

13 ізоедральних шестикутників, що замощують площину

pg (××)		p2 (2222)	p3 (333)	pmg (22*)
pgg (22×)			p31m (3*3)	p2 (2222)	cmm (2*22)	p6m (*632)

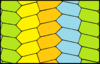
Існує 3 типи моноедральних опуклих гексагональних плиток, які своїми копіями замощують площину. Всі вони ізоедральні. Кожна має параметричні варіації в межах фіксованої симетрії. Тип 2 містить ковзну симетрію та є 2-ізоедральним, що зберігає різні хіральні пари.

3 типи моноедральних опуклих шестикутних паркетів

1	2		3
p2, 2222	pgg, 22×	p2, 2222	p3, 333
b = e B + C + D = 360°	b = e, d = f B + C + E = 360°		a = f, b = c, d = e B = D = F = 120°
2-х плиткова решітка	4-х плиткова решітка		3-х плиткова решітка

Також існують паркети з кількома типами зоногонів.

Замощення чотирикутними і шестикутними зоногонами	Замощення чотирикутними , шестикутними і восьмикутними зоногонами

Див. також

• Гексаграма — шестикутна зірка, утворена двома рівносторонніми трикутниками, є, зокрема, символом юдаїзму.
• Унікурсальна гексаграма
• Шестикутник Лемуана
• Шестикутний паркет
• Шестикутна ґратка
• Гексагональна сингонія
• Шестикутні числа

Посилання

• Weisstein, Eric W. Hexagon(англ.) на сайті Wolfram MathWorld.
• Weisstein, Eric W. Cyclic Hexagon(англ.) на сайті Wolfram MathWorld.
• An Introduction to Hexagonal Geometry on Hexnet a website devoted to hexagon mathematics.
• Hall of Hexagons
• Math is Fun: Hexagon