Група Гейзенберга

У математиці група Гейзенберга $H$ (названа на честь Вернера Гейзенберга) — група верхньотрикутних матриць розмірності $3\times 3$ вигляду

$\left({\begin{matrix}1&a&c\\0&1&b\\0&0&1\end{matrix}}\right),$

де операція множення визначена як множення матриць. Елементи $a$, $b$ і $c$ належать довільному комутативному кільцю з одиницею, в якості якого часто обирають кільце дійсних чисел (в результаті отримують неперервну групу Гейзенберга) або ж кільце цілих чисел (в результаті отримують дискретну групу Гейзенберга).

Неперервна група Гейзенберга з'являється в описі одновимірних систем квантової механіки, особливо в контексті теореми Стоуна–фон Неймана. У загальному випадку групи Гейзенберга можна розглядати у зв'язку з $n$-вимірними системами або ж із довільними симплектичними векторними полями.

Тривимірний випадок

У тривимірному випадку добуток двох матриць Гейзенберга визначається як

$\left({\begin{matrix}1&a&c\\0&1&b\\0&0&1\end{matrix}}\right)\left({\begin{matrix}1&a'&c'\\0&1&b'\\0&0&1\end{matrix}}\right)=\left({\begin{matrix}1&a+a'&c+ab'+c'\\0&1&b+b'\\0&0&1\end{matrix}}\right).$

Як можна побачити з члена $ab'$, ця група неабелева.

Нейтральним елементом (одиницею) групи Гейзенберга є одинична матриця, а обернений визначається наступним чином:

$\left({\begin{matrix}1&a&c\\0&1&b\\0&0&1\end{matrix}}\right)^{-1}=\left({\begin{matrix}1&-a&ab-c\\0&1&-b\\0&0&1\end{matrix}}\right).$

Ця група є підгрупою 2-вимірної афінної групи ${\rm {Aff}}(2)$:

$\left({\begin{matrix}1&a&c\\0&1&b\\0&0&1\end{matrix}}\right),$

дія якої на вектор $({\vec {x}},1)$ відповідає афінному перетворенню

$\left({\begin{matrix}1&a\\0&1\end{matrix}}\right){\vec {x}}+\left({\begin{matrix}c\\b\end{matrix}}\right).$

Є кілька яскравих прикладів тривимірного випадку.

Неперервна група Гейзенберга

Якщо $a$, $b$, $c$ — дійсні числа (в кільці $\mathbb {R}$), то маємо неперервну групу Гейзенберга $H_{3}(\mathbb {R} )$. Це нільпотентна дійсна група Лі розмірності 3.

Додатково до представлення дійсними $3\times 3$ матрицями, неперервна група Гейзенберга має також декілька різних представлень у термінах функціональних просторів. Згідно з теоремою Стоуна–фон Неймана, існує єдине, з точністю до ізоморфізму, незвідне унітарне представлення групи $H$, у якому його центр діє за допомогою заданого нетривіального характеру. Це представлення має декілька важливих застосувань чи моделей. Так, у моделі Шрьодінгера, група Гейзенберга діє на просторі квадратично інтегровних функцій. У тета-представленні вона діє на просторі голоморфних функцій верхньої півплощини; воно назване так на честь зв'язку з тета-функціями.

Дискретна група Гейзенберга

Частина графу Келі дискретної групи Гейзенберга, із генераторами $x$, $y$, $z$ як у тексті. (Кольори використані лише для наочності.)

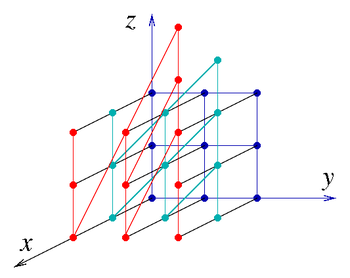
Якщо $a$, $b$, $c$ — цілі числа (в кільці $\mathbb {Z}$), то маємо дискретну групу Гейзенберга $H_{3}(\mathbb {Z} )$. Це неабелева нільпотентна група з двома генераторами

$x=\left({\begin{matrix}1&1&0\\0&1&0\\0&0&1\end{matrix}}\right)$

і

$y=\left({\begin{matrix}1&0&0\\0&1&1\\0&0&1\end{matrix}}\right),$

і зі співвідношеннями

$z=xyx^{-1}y^{-1},\quad xz=zx,\quad yz=zy,$

де

$z=\left({\begin{matrix}1&0&1\\0&1&0\\0&0&1\end{matrix}}\right)$

є генератором центра групи $H_{3}$. (Відмітимо, що обернені до матриць $x$, $y$ і $z$ утворюються заміною $1$ над діагоналлю на $-1$).

Згідно з теоремою Громова (в англомовній літературі — теорема Басса), у цієї групи поліноміальна швидкість зростання порядку 4. Можна генерувати будь-які елементи наступним чином:

$\left({\begin{matrix}1&a&c\\0&1&b\\0&0&1\end{matrix}}\right)=y^{b}z^{c}x^{a}.$

Група Гейзенберга за модулем непарного простого числа $p$

Якщо $a$, $b$, $c$ з $Z/pZ$ для довільного непарного простого $p$, то отримаємо групу Гейзенберга за модулем $p$. Це група порядку $p^{3}$ із генераторами $x$, $y$ та співвідношеннями:

$z=xyx^{-1}y^{-1},\quad x^{p}=y^{p}=z^{p}=1,\quad xz=zx,\quad yz=zy.$

Аналоги групи Гейзенберга над скінченними полями простого непарного порядку $p$ називаються додатковою спеціальною групою або ж, більш точно, додатковою спеціальною групою степеня $p$. Узагальнюючи, якщо похідна підгрупа групи $G$ міститься в центрі $Z$ групи $G$, тоді відображення $G/ZG/Z\rightarrow Z$ є кососиметричним білінійним оператором на абелівських групах.

Однак, умова, щоб $G/Z$ була скінченним векторним простором, вимагає, аби підгрупа Фраттіні групи ${G}$ належала центру групи. А також умова, аби $Z$ був одновимірним векторним простором над $Z/pZ$ вимагає, щоб порядок центра $Z$ дорівнював $p$. Звідки випливає, що якщо група $G$ неабелева, то $G$ — додаткова спеціальна група. Якщо ж група $G$ — додаткова спеціальна група, але не степеня $p$, тоді загальна конструкція при застосуванні до симплектичного векторного простору $G/Z$ не визначає груповий ізоморфізм у $G$.

Група Гейзенберга за модулем 2

Група Гейзенберга за модулем 2 має порядок 8 й ізоморфна діедральній групі $D_{4}$ (група симетрій квадрата). Якщо

$x=\left({\begin{matrix}1&1&0\\0&1&0\\0&0&1\end{matrix}}\right)$

і

$y=\left({\begin{matrix}1&0&0\\0&1&1\\0&0&1\end{matrix}}\right),$

тоді

$xy=\left({\begin{matrix}1&1&1\\0&1&1\\0&0&1\end{matrix}}\right)$

і

$yx=\left({\begin{matrix}1&1&0\\0&1&1\\0&0&1\end{matrix}}\right).$

Елементи $x$ і $y$ відповідають віддзеркаленням (з кутом між ними, що дорівнює $45^{\circ }$), у той час, як $xy$ та $yx$ відповідають поворотам на $90^{\circ }$. Інші віддзеркалення — це $xyx$ і $yxy$, а поворот на $180^{\circ }$ можна представити як $xyxy$ $(=yxyx)$.

Див. також

• Канонічне комутаційне співвідношення
• Перетворення Вігнера-Фейля
• Теорема Стоуна-фон Неймана
• Проективне представлення

Література

• Binz, Ernst; Pods, Sonja (2008). Geometry of Heisenberg Groups. American Mathematical Society. ISBN 978-0-8218-4495-3.
• Hall, Brian C. (2013), Quantum Theory for Mathematicians, Graduate Texts in Mathematics, т. 267, Springer, Bibcode:2013qtm..book.....H, ISBN 978-1461471158
• Hall, Brian C. (2015). Lie Groups, Lie Algebras, and Representations: An Elementary Introduction. Graduate Texts in Mathematics. Т. 222 (вид. second). Springer. ISBN 978-3319134666.
• Howe, Roger (1980). On the role of the Heisenberg group in harmonic analysis. Bulletin of the American Mathematical Society. 3 (2): 821—843. doi:10.1090/s0273-0979-1980-14825-9. MR 0578375.
• Kirillov, Alexandre A. (2004). Ch. 2: "Representations and Orbits of the Heisenberg Group. Lectures on the Orbit Method. American Mathematical Society. ISBN 0-8218-3530-0.
• Mackey, George (1976). The theory of Unitary Group Representations. Chicago Lectures in Mathematics. University of Chicago Press. ISBN 978-0226500522.

Зовнішні посилання

• Groupprops, The Group Properties Wiki Unitriangular matrix group UT(3,p)