Критерій Келлі

Приклад оптимальної частки ставок Келлі порівняно з очікуваним прибутком інших часткових ставок.

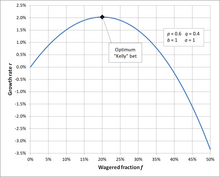
У теорії ймовірностей критерій Келлі (або стратегія Келлі або ставка Келлі) — це формула для визначення розміру ставки. Розмір ставки Келлі визначається шляхом максимізації очікуваного значення логарифма прибутку, що еквівалентно максимізації очікуваного темпу геометричного зростання. Він припускає, що очікуваний прибуток відомий і є оптимальним для гравця, який оцінює свої статки логарифмічно. Джон Ларрі Келлі молодший, дослідник Bell Labs, описав цей критерій у 1956 році. Згідно з заявленими припущеннями, критерій Келлі призводить до більшого кінцевого прибутку, ніж будь-яка інша стратегія в довгостроковій перспективі (тобто, теоретичний максимальний прибуток, коли кількість ставок досягає нескінченності).

Практичне застосування формули було продемонстровано для азартних ігор, і та сама ідея була використана для пояснення диверсифікації в управлінні інвестиціями. У 2000-х роках аналіз у стилі Келлі став частиною основної інвестиційної теорії, було зроблено заяву, що відомі успішні інвестори, зокрема Уоррен Баффет і Білл Гросс, використовують методи Келлі.

Формула для азартних ігор

У випадках, коли програш ставки тягне за собою втрату всієї ставки, коефіцієнт Келлі дорівнює:

$f^{*}=p-{\frac {q}{b}}=p-{\frac {1-p}{b}}$,

де:

• $f^{*}$ — частка поточних активів для ставки.
• $p$ — ймовірність виграшу.
• $q$ — ймовірність програшу ($q=1-p$).
• $b$ — частка ставки, отриманої при виграші. Наприклад, якщо ви робите ставку 10 доларів із коефіцієнтом 2:1 (після виграшу вам повертається 30, тобто ви виграєте 20 доларів), тоді $b=\$20/\$10=2.0$.

  

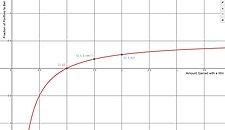
  На малюнку по осі Х відкладається сума, отримана в результаті виграшу, в порівнянні з часткою капіталу для ставок по осі У. Ця цифра передбачає р=0,5 (ймовірність як виграшу, так і програшу становить 50%). Якщо сума виграшу дорівнює 1, то сума ставки Келлі дорівнює 0 доларів, що має сенс у справедливій ставці без очікуваного виграшу.

Наприклад, якщо азартна гра має 60% шансів на виграш ($p=0.6$, $q=0.4$), і гравець отримує коефіцієнти 1 до 1 на виграшну ставку ($b=1$), тоді, щоб максимізувати довгостроковий темп зростання своїх активів, гравець повинен робити ставку 20% від капіталу при кожній нагоді (${\textstyle f^{*}=0.6-{\frac {0.4}{1}}=0.2}$).

На малюнку по осі Х відкладена сума, отримана в результаті виграшу, в порівнянні з часткою капіталу, на яку потрібно зробити ставку по осі У. Ця цифра передбачає р=0,6 (ймовірність виграшу обох гравців становить 60%).

Тривимірна фігура, що представляє оптимальний розмір ставки Келлі (вертикальна вісь) в залежності від ймовірності виграшу та суми, отриманої при виграші.

Якщо гравець має нульову перевагу (тобто якщо $b=q/p$), тоді критерій рекомендує гравцеві нічого не ставити.

Якщо перевага негативна ($b<q/p$), формула дає негативний результат, вказуючи на те, що гравець повинен прийняти іншу сторону ставки. Наприклад, в американській рулетці учаснику ставки пропонується рівний грошовий виграш ($b=1$) на червоне, коли на колесі випадає 18 червоних чисел і 20 не червоних чисел ($p=18/38$). Ставка Келлі дорівнює $-1/19$, що означає, що гравець повинен поставити дев’ятнадцяту частину свого капіталу на те, що червоне не випаде. У рулетці немає явної ставки проти червоних із порівнянними коефіцієнтами, тому найкраще, що може зробити гравець Келлі — це нічого не ставити.

Інвестиційна формула

Більш загальна форма формули Келлі враховує часткові втрати, що актуально для інвестицій:

$f^{*}={\frac {p}{a}}-{\frac {q}{b}},$

де:

• $f^{*}$ — частка активів, яка застосовується до цінного паперу.
• $p$ — ймовірність збільшення вартості інвестицій.
• $q$ — ймовірність того, що вартість інвестицій зменшиться ($q=1-p$).
• $a$ — частка, яка втрачається при негативному результаті. Якщо ціна цінного паперу впаде на 10%, тоді $a=0.1$.
• $b$ — частка, отримана при позитивному результаті. Якщо ціна цінного паперу зросте на 10%, тоді $b=0.1$.

Зверніть увагу, що критерій Келлі дійсний лише для відомих ймовірностей результату, чого не можна сказати про інвестиції. Крім того, інвестори, які не схильні до ризику, не повинні інвестувати всю частку Келлі.

Загальну форму можна переписати таким чином:

$f^{*}={\frac {p}{a}}\left(1-{\frac {1-p}{p}}{\frac {a}{b}}\right)={\frac {p}{a}}\left(1-{\frac {1}{WLP}}{\frac {1}{WLR}}\right),$

де:

• $WLP=p/(1-p)$ — це коефіцієнт ймовірності виграшу до ймовірності програшу (win-loss probability), який є відношенням виграшних ставок до програшних.
• $WLR=b/a$ — це співвідношення виграшів і програшів результатів ставок (win-loss ratio), що є перекосом виграшу.

Зрозуміло, що принаймні один зі коефіцієнтів $WLP$ або $WLR$ має бути більше ніж 1, щоб мати перевагу (тобто $f^{*}>0$). Можливо навіть, що співвідношення ймовірностей виграшу та програшу є несприятливим $WLP<1$, але одне з них має перевагу до тих пір, поки $WLP*WLR>1$.

Формула Келлі може легко призвести до дробів, більших за 1, наприклад, коли розмір втрати $a\ll 1$ (див. наведений вище вираз із коефіцієнтами $WLR$ і $WLP$). Це відбувається дещо суперечливо, оскільки формула дробу Келлі компенсує більший розмір ставки. Але в більшості реальних ситуацій існує велика невизначеність щодо всіх параметрів, які входять у формулу Келлі. У випадку, коли коефіцієнт Келлі перевищує 1, теоретично вигідно використовувати кредитне плече для придбання додаткових цінних паперів з маржею.

Приклад ставки - поведінковий експеримент

У ході дослідження кожному учаснику дали 25 доларів і попросили зробити ставку на рівну суму на монетку, яка випаде орлом в 60% випадків. Учасники мали 30 хвилин на гру, тож могли зробити близько 300 ставок, а максимальний приз становив 250 доларів США. Але поведінка піддослідних була далекою від оптимальної:

Вражаючим є те, що 28% учасників збанкрутували, а середня виплата склала лише $91. Лише 21% учасників досягли максимуму. 18 з 61 учасника поставили все на один кидок, тоді як дві третини поставили на решку на якомусь етапі експерименту.

Використовуючи критерій Келлі та ґрунтуючись на коефіцієнтах в експерименті (не враховуючи обмеження в 250 доларів США та кінцеву тривалість тесту), правильним підходом було б поставити 20% свого капіталу на кожен кидок монети, що дає середній виграш в 2,034% в кожному раунді. Це середнє геометричне, а не арифметична норма в 4% ($r=0,2\cdot (0,6-0,4)=0,04)$. Теоретично очікуваний прибуток після 300 раундів становив би 10 505 доларів ($25\cdot (1.02034)^{300}$), якби він не був обмежений.

У цій конкретній грі, через ліміт, стратегія, яка полягає у тому, щоб ставити тільки 12% капіталу на кожне підкидання дасть ще кращі результати (95% ймовірність досягнення ліміту та середня виплата $242,03).

Доведення

Евристичні докази критерію Келлі прості. Критерій Келлі максимізує очікуване значення логарифма прибутку (очікуване значення функції визначається сумою ймовірності кожного конкретного результату, помноженої на значення функції в разі досягнення такого результату за всіма можливими результатами). Ми починаємо з 1 одиниці капіталу і ставимо частку $f$ цього капіталу на результат, який станеться з імовірністю $p$ та коефіцієнтом виграшу $b$. Імовірність виграшу становить $p$, і в цьому випадку отриманий статок дорівнює $1+fb$. Імовірність програшу дорівнює $q=1-p$, а ймовірність негативного результату дорівнює $a$ . У цьому випадку кінцевий статок дорівнює $1-fa$. Отже, очікувана геометрична швидкість зростання $r$ дорівнює:

$r=(1+fb)^{p}\cdot (1-fa)^{q}$.

Ми хочемо знайти максимальне r цієї кривої (як функцію f), що передбачає знаходження похідної рівняння. Це легше зробити, якщо спочатку взяти логарифм кожної сторони. Отримане рівняння:

$E=\log(r)=p\log(1+fb)+q\log(1-fa)$.

$E$ позначає логарифмічне зростання статку. Щоб знайти значення $f$ для яких швидкість зростання є максимальною, позначається як $f^{*}$, ми диференціюємо наведений вище вираз і встановлюємо його рівним нулю. Отримуємо:

$\left.{\frac {dE}{df}}\right|_{f=f^{*}}={\frac {pb}{1+f^{*}b}}+{\frac {-qa}{1-f^{*}a}}=0$

Перегруповуємо це рівняння, щоб знайти значення $f^{*}$, яке дає критерій Келлі:

$f^{*}={\frac {p}{a}}-{\frac {q}{b}}$

Зверніть увагу, що цей вираз зводиться до простої формули азартної гри, коли $a=1=100\%$, а програш призводить до повної втрати ставки.

Бернуллі

У статті 1738 року Даніель Бернуллі запропонував, що, коли є вибір ставок чи інвестицій, слід вибирати те, що має найвище середнє геометричне значення результатів. Математично це еквівалентно критерію Келлі, хоча мотивація інша (Бернуллі хотів вирішити Санкт-Петербурзький парадокс).

Англійський переклад статті Бернуллі був опублікований лише в 1954 році, але ця робота була добре відома серед математиків та економістів.

Застосування на фондовому ринку

У математичних фінансах, якщо вага цінних паперів максимізує очікуваний геометричний темп зростання (що еквівалентно максимізації логарифмічного капіталу), тоді інвестиційний портфель є оптимальним для зростання.

Розрахунки оптимального зростання портфелів акцій можуть призвести до величезних проблем, пов'язаних з невірними вхідними даними та неправильними результатами. Наприклад, у наведених нижче випадках розглядається очікувана прибутковість і коваріаційна структура активів, але ці параметри є в найкращому випадку оцінками або моделями, які мають значну невизначеність. Якщо ваги портфеля є значною мірою функцією помилок оцінки, то фактичні показники портфеля з оптимальним зростанням можуть фантастично відрізнятися від очікуваного прогнозу. Невизначеність параметрів і помилки оцінки є великою темою в портфельній теорії. Підхід до запобігання невідомому ризику полягає в тому, щоб інвестувати менше, ніж критерій Келлі.

Приблизні оцінки все ще корисні. Якщо взяти надлишковий прибуток 4% і волатильність 16%, то річний коефіцієнт Шарпа та коефіцієнт Келлі, за розрахунками складуть 25% і 150%. Денний коефіцієнт Шарпа та коефіцієнт Келлі становить 1,7% і 150%. Коефіцієнт Шарпа передбачає ймовірність щоденного виграшу $p=(50\%+1,7\%/4)$, де ми припустили, що пропускна здатність ймовірності становить $4\sigma =4\%$. Тепер ми можемо застосувати дискретну формулу Келлі для $f^{*}$ вище з $p=50.425\%,a=b=1\%$, і ми отримуємо іншу приблизну оцінку для коефіцієнта Келлі $f^{*}=85\%$. Обидві ці оцінки коефіцієнта Келлі виглядають цілком обґрунтованими, однак розумний підхід передбачає подальше множення коефіцієнта Келлі на 50% (тобто половину Келлі).

У докладній статті Едварда О. Торпа та його співавтора коефіцієнт Келлі становить 117% для індексу SP500 американського фондового ринку. Значний хвостовий ризик зниження для фондових ринків є ще однією причиною зменшити частку Келлі від наївної оцінки (наприклад, зменшити до половини коефіцієнта Келлі).

Критика

Хоча обіцянка стратегії Келлі досягти кращих результатів, ніж будь-яка інша стратегія в довгостроковій перспективі, здається переконливою, деякі економісти рішуче виступають проти неї, головним чином тому, що конкретні інвестиційні обмеження людини можуть переважити бажання оптимальних темпів зростання. Загальноприйнятою альтернативою є теорія очікуваної корисності, яка стверджує, що розмір ставок повинен бути таким, щоб максимізувати очікувану корисність результату (для людини з логарифмічною корисністю ставка Келлі максимізує очікувану корисність, тому немає конфлікту; щобільше, в оригінальній статті Келлі чітко зазначено, що потреба у функції корисності у випадку азартних ігор, у які грають кінцеву кількість разів). Навіть прихильники Келлі зазвичай виступають за дробовий Келлі (ставка на фіксовану частку суми, рекомендованої Келлі) з низки практичних міркувань, таких як бажання зменшити волатильність або захист від недетермінованих помилок у їхніх розрахунках виграшу. Говорячи просторіччям, критерій Келлі вимагає точних значень ймовірності, що не завжди можливо для результатів реальних подій. Коли гравець переоцінює свою справжню ймовірність виграшу, розраховане значення критерію буде відрізнятися від оптимального, збільшуючи ризик банкрутства.

Формулу Келлі можна розглядати як «часову диверсифікацію», яка передбачає прийняття однакового ризику протягом різних послідовних періодів часу (на відміну від прийняття однакового ризику в різних активах для диверсифікації активів). Існує чітка різниця між диверсифікацією часу та диверсифікацією активів, яку підняв Пол А. Самуельсон. Існує також різниця між усередненням по ансамблю (розрахунок корисності) і усередненням за часом (ставки Келлі на кілька періодів за один часовий шлях у реальному житті). Дискусія була поновлена, викликавши порушення ергодичності. Проте слід визнати різницю між порушенням ергодичності та лицарською невизначеністю.

Вища математика

Переконливі та загальні докази можна знайти в оригінальній статті Келлі або в деяких інших посиланнях, перелічених нижче. Деякі виправлення були опубліковані. Наведемо наступний нестрогий аргумент для випадку з $b=1$ (ставка 1:1 на "рівні гроші"), щоб показати загальну ідею та надати деяку інформацію. Коли $b=1$, учасник парі Келлі робить ставку $2p-1$ разів їх початковий статок $W$, як показано вище. Якщо вони виграють, то виграють $2pW$ після однієї ставки. Якщо вони програють, вони програють $2(1-p)W$. Припустимо, вони роблять $N$ ставок подібним чином і виграють $K$ рази з цієї серії $N$ ставок. Кінцевий виграш складе:

$2^{N}p^{K}(1-p)^{N-K}W\!.$

Порядок виграшів і програшів не впливає на підсумковий виграш. Припустимо, що інший гравець робить ставку на іншу суму, $(2p-1+\Delta )W$ для деякого значення $\Delta$ (де $\Delta$ може бути позитивним або негативним). Вони матимуть $(2p+\Delta )W$ після перемоги і $[2(1-p)-\Delta ]W$ після поразки. Після такої ж серії виграшів і поразок, як і учасник парі Келлі, вони матимуть:

$(2p+\Delta )^{K}[2(1-p)-\Delta ]^{N-K}W$

Візьмемо похідну цього за $\Delta$ і отримаємо:

$K(2p+\Delta )^{K-1}[2(1-p)-\Delta ]^{N-K}W-(N-K)(2p+\Delta )^{K}[2(1-p)-\Delta ]^{N-K-1}W$

Функція досягає максимуму, коли ця похідна дорівнює нулю, що відбувається при:

$K[2(1-p)-\Delta ]=(N-K)(2p+\Delta )$

це означає, що

$\Delta =2({\frac {K}{N}}-p)$

але частка виграшних ставок в кінцевому підсумку за слабким законом великих чисел наблизиться до:

$\lim _{N\to +\infty }{\frac {K}{N}}=p$

Таким чином, у довгостроковій перспективі, остаточний виграш максимізується шляхом налаштування $\Delta$ до нуля, що означає дотримання стратегії Келлі. Це ілюструє те, що Келлі має як детерміновані, так і стохастичні компоненти. Якщо хтось знає K і N та бажає вибрати постійну частку капіталу для ставок кожного разу (інакше можна схитрувати, наприклад, поставити нуль після K-го виграшу, знаючи, що решта ставок буде програшною), в результаті у нього буде більше грошей, якщо він щоразу робитиме ставку:

$(2{\frac {K}{N}}-1)W$

Це вірно незалежно від того $N$ маленький чи великий. «Довгострокова» частина Келлі необхідна, тому що $K$ невідомо заздалегідь, а лише те, що зі збільшенням $N$, $K$ наближатиметься до $pN$. Той, хто ставить більше, ніж Келлі, може зробити краще, якщо $K>pN$ на відрізку; той, хто ставить менше, ніж Келлі, може зробити краще, якщо $K<pN$ на відрізку, але в довгостроковій перспективі Келлі завжди виграє. Евристичний доказ для загального випадку відбувається наступним чином. В одному випробуванні, якщо інвестувати частку $f$ свого капіталу, якщо стратегія є виграшною, капітал наприкінці випробування збільшується на коефіцієнт $1-f+f(1+b)=1+fb$, і, так само, якщо стратегія зазнає невдачі, капітал зменшується на коефіцієнт $1-fa$. Таким чином наприкінці $N$ випробування (з $pN$ успіхів і $qN$ невдач), стартовий капітал у розмірі 1 долара дає:

$C_{N}=(1+fb)^{pN}(1-fa)^{qN}.$

Максимізація $\log(C_{N})/N$, а отже $C_{N}$,щодо до $f$ призводить до бажаного результату.

$f^{*}=p/a-q/b.$

Едвард О. Торп надав більш детальне обґрунтування цієї формули для загального випадку. Там видно, що заміна $p$ на відношення кількості «успіхів» до кількості випробувань означає, що кількість випробувань має бути дуже великим числом, оскільки $p$ визначається як границя цього відношення, коли кількість випробувань досягає нескінченності. Коротко кажучи, ставки $f^{*}$ кожен раз, швидше за все, максимізує темпи зростання капіталу лише у випадку, коли кількість випробувань дуже велика, а $p$ і $b$ однакові для кожного випробування. На практиці це означає грати в ту саму гру знову і знову, де ймовірність та коефіцієнт виграшу завжди однакові. В евристичному доказі вище, $pN$ і $qN$ високоймовірні лише для дуже великих $N$.

Ігри з декількома результатами

Критерій Келлі можна узагальнити для азартних ігр з багатьма несумісними результатами, наприклад, у скачках. Припустимо, що є кілька взаємовиключних результатів. Ймовірність того, що $k$ -й кінь виграє перегони $p_{k}$, загальна сума ставок на $k$-ий коня є $B_{k}$, і

$\beta _{k}={\frac {B_{k}}{\sum _{i}B_{i}}}={\frac {D}{1+Q_{k}}},$

де $Q_{k}$ це коефіцієнти виплати. $D=1-tt$, ставка дивідендів, де $tt$ – дорожній збір або податок, ${\frac {D}{\beta _{k}}}$ це ставка доходу після вирахування ставки, коли $k$ -й кінь перемагає. Частка коштів гравця, на яку потрібно зробити ставку $k$ -ий кінь є $f_{k}$. Критерій Келлі для азартних ігор із кількома взаємовиключними результатами дає алгоритм для знаходження оптимального набору $S^{o}$ результатів, на які доцільно робити ставки, і дає чітку формулу для знаходження оптимальних часток $f_{k}^{o}$ статку гравця, на який потрібно зробити ставку на результати, включені в оптимальний набір $S^{o}$. Алгоритм оптимального набору результатів складається з чотирьох кроків:

1. Обчислити очікувану норму доходу для всіх можливих (або лише для кількох найбільш перспективних) результатів: $er_{i}={\frac {Dp_{i}}{\beta _{i}}}=p_{i}(Q_{i}+1)$.
2. Змінити порядок результатів, щоб отримати нову послідовність $er_{k}$(не зростає). Таким чином $er_{1}$ буде найкращим вибором.
3. Встановити $S=\varnothing$ (порожній набір), $k=1$, $R(S)=1$ . Таким чином, найкращий вибір $er_{k}=er_{1}$ буде розглянутий першим.
4. Повтори:

   Якщо $er_{k}={\frac {D}{\beta _{k}}}p_{k}>R(S)$, вставити $k$ -й результат у набір: $S=S\cup \{k\}$, перерахувати $R(S)$ за формулою: $R(S)={\frac {D\sum _{k\notin S}p_{k}}{D-\sum _{k\in S}\beta _{k}}}$, а потім встановити $k=k+1$. В іншому випадку встановити $S^{o}=S$ і припинити повторення.

Якщо оптимальний набір $S^{o}$ порожній, тоді взагалі не робіть ставки. Якщо набір $S^{o}$ оптимальних результатів не порожній, то оптимальний коефіцієнт $f_{k}^{o}$ для ставки на $k$ -й результат може бути розрахована за цією формулою:

$f_{i}=p_{i}-\beta _{i}{\frac {\sum _{k\notin S}p_{k}}{\left(D-\sum _{k\in S}\beta _{k}\right)}}.$

Можна довести , що

$R(S^{o})=1-\sum _{i\in S^{o}}{f_{i}^{o}},$

де права частина – резервна ставка. Тому вимогу $er_{k}={\frac {D}{\beta _{k}}}p_{k}>R(S)$ можна інтерпретувати наступним чином: $k$ -й результат входить до набору $S^{o}$ оптимальних результатів тоді і тільки тоді, коли його очікувана норма доходу більша за резервну ставку. Формулу оптимального коефіцієнта $f_{k}^{o}$ можна інтерпретувати як перевищення очікуваної норми доходу $k$ -го коня над резервною ставкою, поділеною на дохід за вирахуванням ставки коли $k$ -й кінь перемагає або як перевищення ймовірності $k$ -й виграшу коня за резервною ставкою, поділеною на дохід після вирахування ставки, коли $k$ -й кінь перемагає. Двійковий показник зростання дорівнює:

$G^{o}=\sum _{i\in S}{p_{i}{\dot {l}}og_{2}(er_{i})}+(1-\sum _{i\in S}{p_{i}})log_{2}(R(S^{0})),$

а час подвоєння становить

$T_{d}={\frac {1}{G^{o}}}.$

Цей метод вибору оптимальних ставок може бути застосований також в тих випадках коли ймовірності $p_{k}$ відомі лише для кількох найбільш перспективних результатів, а решта результатів не мають шансів на перемогу. В цьому випадку так і повинно бути, що

$\sum _{i}{p_{i}}<1,$ та

$\sum _{i}{\beta _{i}}<1$ .

Фондові інвестиції

Поліном Тейлора другого порядку можна використовувати як хороше наближення основного критерію. У першу чергу це корисно для інвестицій в акції, де частка, присвячена інвестиціям, базується на простих характеристиках, які можна легко оцінити на основі наявних історичних даних – очікувана вартість і дисперсія. Це наближення дає результати, які є надійними та дають результати, подібні до вихідного критерію.

Для окремих активів (акції, індексних фондів тощо) і безризикової ставки легко отримати оптимальну частку для інвестування за допомогою геометричного броунівського руху. Стохастичне диференціальне рівняння, що керує еволюцією логарифмічного нормально розподіленого активу $S$ вчасно $t$ ( $S_{t}$ ) є

$dS_{t}/S_{t}=\mu dt+\sigma dW_{t}$

чий розв'язок

$S_{t}=S_{0}\exp \left(\left(\mu -{\frac {\sigma ^{2}}{2}}\right)t+\sigma W_{t}\right)$

де $W_{t}$ є вінерівським процесом, і $\mu$ (відсотковий дрейф) і $\sigma$ (відсоток волатильності) є константами. Приймаючи очікування логарифма:

$\mathbb {E} \log(S_{t})=\log(S_{0})+\left(\mu -{\frac {\sigma ^{2}}{2}}\right)t.$

Тоді очікуваний логарифм повертає $R_{s}$, що дорівнює

$R_{s}=\left(\mu -{\frac {\sigma ^{2}}{2}}\,\right)s.$

Розглянемо портфель, який складається з активів $S$ і безризикова ставка виплати облігацій $r$, з коефіцієнтом $f$ інвестовано в $S$ і $(1-f)$ в облігації. Вищезгадане рівняння для $dS_{t}$ має бути змінено цим коефіцієнтом, тобто $dS_{t}'=f*dS_{t}$, із відповідним рішенням

$S'_{t}=S'_{0}\exp \left(\left(f\mu -{\frac {(f\sigma )^{2}}{2}}\right)t+f\sigma W_{t}\right)$

очікуваний одноперіодний прибуток визначається як

$\mathbb {E} {\left(\left[{\frac {S'_{1}}{S'_{0}}}-1\right]+(1-f)r\right)}=\mathbb {E} {\left(\left[\exp \left(\left(f\mu -{\frac {(f\sigma )^{2}}{2}}\right)+f\sigma W_{1}\right)-1\right]\right)}+(1-f)r$

Для маленьких $\mu$, $\sigma$, і $W_{t}$, рішення можна розширити до першого порядку, щоб отримати приблизне збільшення статків

$G(f)=f\mu -{\frac {(f\sigma )^{2}}{2}}+((1-f)\ r).$

Знайшовши $\max(G(f))$ ми отримуємо

$f^{*}={\frac {\mu -r}{\sigma ^{2}}}.$

$f^{*}$– це коефіцієнт, який максимізує очікуваний логарифмічний результат, а отже, це коефіцієнт Келлі. Торп прийшов до того самого результату, але через інший висновок. Пам'ятайте, що $\mu$ відрізняється від прибутковості портфеля активів $R_{s}$. Плутання з цим є поширеною помилкою вебсайтів і статей, де йдеться про критерій Келлі.

Для кількох активів розглянемо ринок із $n$ корельованих акцій $S_{k}$ зі стохастичними прибутками $r_{k}$, $k=1,\dots ,n$ і безризиковою облігацією з дохідністю $r$. Інвестор вкладає частку $u_{k}$ свого капіталу в $S_{k}$, а решту – в облігацію. Без втрати загальності припустимо, що стартовий капітал інвестора дорівнює 1. Відповідно до критерію Келлі слід максимізувати

$\mathbb {E} \left[\ln \left((1+r)+\sum \limits _{k=1}^{n}u_{k}(r_{k}-r)\right)\right].$

Розширюючи це рядом Тейлора навколо ${\vec {u_{0}}}=(0,\ldots ,0)$, ми отримаємо:

$\mathbb {E} \left[\ln(1+r)+\sum \limits _{k=1}^{n}{\frac {u_{k}(r_{k}-r)}{1+r}}-{\frac {1}{2}}\sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}u_{k}u_{j}{\frac {(r_{k}-r)(r_{j}-r)}{(1+r)^{2}}}\right].$

Таким чином, ми зводимо задачу оптимізації до квадратичного програмування, і це необмежене рішення є

${\vec {u^{\star }}}=(1+r)({\widehat {\Sigma }})^{-1}({\widehat {\vec {r}}}-r)$

де ${\widehat {\vec {r}}}$ і ${\widehat {\Sigma }}$ – вектор середніх і матриця других змішаних нецентральних моментів надлишкової прибутковості. Існує також числовий алгоритм для дробових стратегій Келлі та для оптимального рішення без кредитного плеча та без обмежень щодо коротких продажів.