Експоненційний запис
Експоненці́йний за́пис[1], експоненці́йне предста́влення[2], експоненці́йна фо́рма за́пису[2][3], експоненці́йний фо́рмат[4] (також експоненціа́льний[5], науко́вий за́пис[6]; англ. scientific notation, іноді exponential notation) — представлення дійсних чисел у вигляді мантиси і порядку. Зручний при представленні дуже великих і дуже малих чисел, а також для уніфікації їх написання.
Число , де
- N — число, що записують;
- М — мантиса;
- n — основа показникової функції;
- p (ціле) — порядок (показник степеня);
- — характеристика числа.
Приклади[ред. | ред. код]
- 1 000 000 (один мільйон): — тут N = 1 000 000, M = 1,0, n = 10, p = 6.
- 1 201 000 (один мільйон двісті одна тисяча): — тут N = 1 201 000, M = 1,201, n = 10, p = 6.
- −1 246 145 000 (мінус один мільярд двісті сорок шість мільйонів сто сорок п'ять тисяч): — тут N = −1 246 145 000, M = −1,246145, n = 10, p = 9.
- 0,000001 (одна мільйонна): — тут N = 0,000001, M = 1,0, n = 10, p = −6.
- 0,000000231 (двісті тридцять одна мільярдна): — тут N = 0,000000231, M = 2,31, n = 10, p = −7.
Нормалізований запис[ред. | ред. код]
| Стандартний десятковий запис | Нормалізований запис |
|---|---|
| 2 | 2×100 |
| 300 | 3×102 |
| 4,321.768 | 4.321768×103 |
| −53,000 | −5.3×104 |
| 6,720,000,000 | 6.72×109 |
| 0.2 | 2×10−1 |
| 0.000 000 007 51 | 7.51×10−9 |
Будь-яке число може бути записане у вигляді багатьма способами. Наприклад, число 350 може бути записане як , або , або .
У нормалізованому науковому записі порядок вибирається так, щоб абсолютна величина залишалась не менше одиниці, але строго менше десяти . Наприклад, 350 записується як . Цей вигляд запису дає змогу легко порівнювати два числа.
В інженерному нормалізованому записі (зокрема в інформатиці) мантиса зазвичай вибирається в межах : .
У деяких калькуляторах передбачена додаткова функція — запис із мантисою і порядком, кратним 3. Так, наприклад, три цілих п'ятдесят дві соті сто мільйонних записується як тридцять п'ять цілих дві десяті мільярдних. Такий запис простий для читання легше прочитати, як «640 мільйонів», ніж і зручний для виразу фізичних величин в одиницях вимірювання.
Комп'ютерний спосіб експоненційного запису[ред. | ред. код]
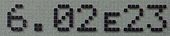
Вважатимемо, що n = 10.
На комп'ютері, зокрема в тексті комп'ютерних програм, експоненційний запис записують у вигляді MEp, де:
- М — мантиса;
- E — буква E (від англ. exponent), що означає «◻⋅10◻» («...помножити на десять у степені…»);
- p — порядок.
Приклади[ред. | ред. код]
У програмуванні часто використовують символ «+» для невід'ємного порядку і передні нулі, а як десятковий роздільник — крапку:
.
Для покращення читабельності іноді використовують малу літеру e: .
Див. також[ред. | ред. код]
Примітки[ред. | ред. код]
- ↑ запис // Англійсько-українсько-англійський словник наукової мови (фізика та споріднені науки). Частина ІІ українсько-англійська / уклад. О. Кочерга, Є. Мейнарович. — 2010.
- ↑ а б notation // Англійсько-український словник з математики та інформатики / уклад. Є. Мейнарович, М. Кратко. — 2010.
- ↑ notation // Англійсько-українсько-англійський словник наукової мови (фізика та споріднені науки). Частина І англійсько-українська / уклад. О. Кочерга, Є. Мейнарович. — 2010.
- ↑ формат // Українсько-англійський словник з радіоелектроніки / Богдан Рицар, Леонід Сніцарук, Роман Мисак. — 2015.
- ↑ експоненціа́льний // Словник української мови : у 20 т. — К. : Наукова думка, 2010—2022.
- ↑ науковий запис // Глосарій термінів з хімії / Й. Опейда, О. Швайка. — 2007.
| ||||||||||||||

























