Показникова функція
| Показникова функція | |
 | |
| Область значень | множина додатних дійсних чиселd |
|---|---|
| Підтримується Вікіпроєктом | Вікіпедія:Проєкт:Математика |
| Протилежне | логарифм |
| | |
Показнико́ва, або експоненці́йна фу́нкція (англ. exponential function) — функція виду , де — стале число (додатне, але відмінне від одиниці).
У дійсному випадку основа степеня — деяке додатне дійсне число, а аргументом функції є дійсний показник степеня.
Показникова функція узагальнюється в теорії комплексних функцій, де аргумент і показник степеня можуть бути довільними комплексними числами.
У найзагальнішому вигляді — , введена Лейбніцем 1695 року.
Особливо виділяється випадок, коли як основа степеня виступає число e. Така функція називається експоне́нтою (дійсною або комплексною).
Визначення[ред. | ред. код]
Нехай — додатне дійсне число, — раціональне число: . Тоді визначається за такими правилами.
- Якщо , то .
- Якщо , то .
- Якщо , то (для ).
Показникову функцію можливо визначити багатьма еквівалентними способами. Зазвичай її визначають за допомогою наступного степеневого ряду:[1]
Оскільки радіус збіжності цього степеневого ряду є нескінченним, це визначення застосовується для всіх комплексних чисел . Сталу e можна визначити як .
Для довільного дійсного показника значення можна визначити як границю послідовності , де — раціональні числа, що сходяться до . Для експоненти є й інші визначення через границю, наприклад:
Основні властивості[ред. | ред. код]
Дійсну показникову функцію визначено на всій дійсній осі більше нуля. При вона всюди зростає; при функція спадає на всій області визначення.
Виконуються тотожності
- ;
- ;
- .
Зворотна функція до показникової функції — логарифм.
Показникова функція росте на нескінченності швидше будь-якої степеневої:
Показникова функція нескінченно диференційована, її похідною є
Експонента[ред. | ред. код]

Експонента () — функція , де e — основа натурального логарифма ( — число Ейлера).
Властивості[ред. | ред. код]
Експонента є визначеною на всій дійсній осі. Вона усюди зростає й є більшою за нуль. Зворотною функцією до неї є натуральний логарифм.
Експонента є нескінченно диференційованою. Її похідна в точці нуль дорівнює «1», тому дотична в цій точці проходить під кутом 45°.
Основна функціональна властивість експоненти: . Неперервна функція з такою властивістю або тотожно дорівнює 0, або має вид , де — деяка стала.
Формальне визначення[ред. | ред. код]

Експоненційну функцію може бути означено двома еквівалентними способами. Через ряд Тейлора:
або через границю:
Тут x — довільне дійсне, комплексне, p-адичне число або обмежений лінійний оператор.
Комплексна експонента[ред. | ред. код]

Легенда
Комплексна експонента — математична функція, що означується співвідношенням , де є комплексним числом. Комплексна експонента означується як аналітичне продовження експоненти дійсної змінної :
Означмо формальний вираз
.
Означений таким чином вираз на дійсній осі буде збігатися з класичною дійсною експонентою. Для повної коректності побудови необхідно довести аналітичність функції , тобто показати, що розкладається в деякий збіжний до даної функції ряд. Покажемо це:
Збіжність даного ряду легко доводиться:
.
Ряд усюди збігається абсолютно, тобто взагалі всюди збігається, таким чином, сума цього ряду в кожній конкретній точці буде визначати значення аналітичної функції . Відповідно до теореми єдиності, отримане продовження буде єдиним, отже, на комплексній площині функція є всюди визначеною й аналітичною.
Властивості[ред. | ред. код]
- Комплексна експонента — ціла голоморфна функція на всій комплексній площині. Вона в жодній точці не обертається на нуль.
- — періодична функція з основним періодом 2πi: . Через періодичність комплексна експонента має безліч листів. Як її однолисну область можна вибрати будь-яку горизонтальну смугу висотою .
- — єдина функція, похідна (а також, відповідно, й інтеграл) якої дорівнює їй самій.
- Алгебрично експоненту від комплексного аргументу може бути визначено наступним чином:
- Зокрема, має місце (тотожність Ейлера)
- Зокрема, має місце (тотожність Ейлера)
Графіки функції[ред. | ред. код]
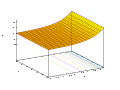
Показникова функція відображує будь-яку пряму в комплексній площині у логарифмічну спіраль на комплексній площині з центром в початку координат. Необхідно відмітити два особливі випадки: коли початкова пряма є паралельною до осі дійсних чисел, отримувана в результаті спіраль ніколи не замикається в собі; коли пряма є паралельною осі уявних чисел, отримувана в результаті спіраль є колом із деяким радіусом.
- Графіки показникової функції у комплексній площині
-
z = Re(ex + iy)
-
z = Im(ex + iy)
-
Примітки[ред. | ред. код]
- ↑ Rudin, Walter (1987). Real and complex analysis (PDF) (вид. 3rd). New York: McGraw-Hill. с. 1. ISBN 978-0-07-054234-1. (англ.)
Література[ред. | ред. код]
- С. Т. Завало (1972). Елементи аналізу. Алгебра многочленів. Київ: Радянська школа.
- Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2023. — 1900+ с.(укр.)
Посилання[ред. | ред. код]
- Показникова функція // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 179. — 594 с.
- «Експонента і число е: просто і зрозуміло» [Архівовано 22 грудня 2016 у Wayback Machine.] (рос.) — переклад статті «An Intuitive Guide To Exponential Functions & e | BetterExplained» [Архівовано 23 червня 2007 у Wayback Machine.] (англ.)
- Способи розв'язання показникових рівнянь[недоступне посилання з липня 2019]








![{\displaystyle a^{x}={\sqrt[{n}]{a^{m}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f7ed005a337fcce2a069abf6e36733907f1915b)