Відстань до Місяця

Матеріал з Вікіпедії — вільної енциклопедії.
Перейти до навігації Перейти до пошуку
одиниця відстані
Відстань до Місяця
Відстанню до Місяця (384402 км) називають середню відстань між Землею й Місяцем. Фактична відстань змінюється позаяк Місяць обертається навколо Землі. На зображенні зіставлені видимі кутові розміри Місяця, коли він перебуває в найближчій і найдальшій точці відносно Землі.
Загальна інформація
Система одиниць Астрономія
Одиниця Відстань
Позначення LD або 
Перерахунок в інші системи
1 LD в... дорівнює...
   Основні одиниці SI    384402×103 м
   Метрична система    384402 км
   Астрономічна одиниця    0.002569 а. о.


Відстань до Місяця (LD або ), яку називають також відстань між Землею та Місяцем — це одиниця виміру в астрономії. Є середньою відстанню від центру Землі до центру Місяця. Кажучи математично, це середня велика піввісь геоцентричної орбіти Місяця. Відстанню до Місяця можуть також називати усереднену за часом відстань між центрами Землі та Місяця або, ще точніше, миттєву відстань Земля — Місяць.

Відстань до Місяця дорівнює приблизно 400 000 км, або 250 000 миль.

Середня довжина великої півосі дорівнює 384 402 км[1]. Середня за часом відстань між центрами Землі та Місяця становить 385 000,6 км. Фактична відстань коливається залежно від положення Місяця на орбіті від 356 500 км у перигеї до 406 700 в апогеї. Різниця між цими величинами становить 50 200 км[2].

Відстань до Місяця зазвичай використовують для вимірювання відстаней до навколоземних об'єктів[3]. Крім того, вона є важливим астрономічним показником; її вимірювання з точністю кілька частин на трильйон має значення для тестування теорій гравітації, як-от загальна теорія відносності[4], та для уточнення інших астрономічних величин, як-от маса Землі[5], радіус Землі[6] та обертання Землі[7]. Вимірювання також корисне для характеристики діаметра Місяця, маси Сонця та відстані до Сонця.

Вимірювання відстані до Місяця з точністю до міліметрів здійснюються шляхом вимірювання часу, необхідного світлу для проходження між лідарними станціями на Землі та ретрорефлекторами, розміщеними на Місяці.

За допомогою лазерної локації Місяця виявлено, що Місяць віддаляється від Землі по спіралі із середньою швидкістю 3,8 см на рік[8][9][10].

Величини

[ред. | ред. код]
Відстань між Землею та Місяцем — розміри та відстань у масштабі.
Відстань до Місяця, виражена у вибраних одиницях
Одиниця Середнє значення Невизначеність Реф
Метр 3,84402×108 1,1 мм [1]
Кілометр 384 402 1,1 мм [1]
Миля 238 856 0,043 дюйма [1]
Радіус Землі 60,32 [11]
Астрономічна величина 1/388,6 = 000257 [12][13]
Світлова секунда 1,282 37,5 пікосекунди [1]
  • Одна астрономічна величина дорівнює 389 відстаням до Місяця[14].
  • Один світловий рік дорівнює 24611700 відстаням до Місяця[14][15].
  • Радіус геостаціонарної орбіти становить 42,164 км від центру Землі або 35,786 км від поверхні Землі. Перша величина дорівнює 1/9,117 = 0,10968 відстані до Місяця.

Коливання

[ред. | ред. код]

Миттєва відстань до Місяця постійно змінюється. Оскільки орбіта не є круговою, реальна відстань між Місяцем і Землею може змінюватися на 75 м/с[2], тобто понад 1000 км лише за 6 годин[16]. Існують також інші ефекти, які впливають на відстань до Місяця. Деякі фактори описані в цьому розділі.

Пертурбації й ексцентриситет

[ред. | ред. код]

Відстань до Місяця можна виміряти з точністю до 2 мм протягом 1-годинного періоду вимірювань[17], що зумовлює загальну невизначеність 2—3 см для середньої відстані. Однак внаслідок еліптичності орбіти зі змінним ексцентриситетом миттєва відстань змінюється з місячною періодичністю.

Крім того, відстань збурюється гравітаційним впливом різних астрономічних тіл, найбільше — Сонця, дещо менше — Юпітера. Іншими силами, хвилинні збурення зумовлюються гравітаційним тяжінням до інших планет Сонячної системи та астероїдів; припливам та релятивістськими ефектами[18]. На відстань до Місяця впливає також тиск випромінювання від Сонця, змінюючи її на величину ±3,6 мм[17].

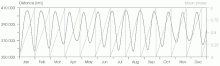
Хоча миттєва невизначеність становить менше міліметра, протягом типового місяця вимірювана відстань до Місяця може змінюватися більше ніж на 21 000 км від середнього значення. Ці збурення добре відомі[19], і відстань до Місяця можна точно розрахувати на тисячі років вперед[18].

Відстань до Місяця, зіставлена з фазами Землі та Місяця у 2014 році. Фази місяця: 0 (1) — новий Місяць (молодик), 0,25 — перша чверть, 0,5 — повний Місяць, 0,75 — остання чверть.
Коливання відстані між центрами Місяця та Землі за 700 днів.

Припливне розсіювання

[ред. | ред. код]

Унаслідок дії припливних сил кутовий імпульс обертання Землі повільно переноситься на орбіту Місяця[20]. Через це швидкість обертання Землі повільно зменшується (зі швидкістю 2,3 мілісекунди на століття)[21], а орбіта Місяця поступово розширюється. Поточна швидкість цього розширення — 3,805 ± 0,004 мм на рік[19]. Однак існує думка, що цей показник останнім часом збільшився, оскільки значення 3,8 означало б, що Місяцю лише 1,5 млрд років, тоді як майже всі науковці погоджуються з тим, що його вік — прибл. 4 млрд років[22]. Вважається також, що цей аномально високий темп віддалення може прискорюватися[23].

Прогнозується, що відстань до Місяця продовжуватиме збільшуватися, доки (теоретично) Земля і Місяць не увійдуть у припливне захоплення — тобто доки вони не почнуть обертатися синхронно, як і Плутон і Харон, будучи постійно повернуті одне до одного одним боком. Це трапиться, коли тривалість місячного орбітального періоду зрівняється з періодом обертання Землі, який, за оцінками, становитиме 47 наших сучасних днів. Тоді обидва тіла увійдуть у стан рівноваги, і подальше передавання обертальної енергії не відбуватиметься. Однак моделі передбачають, що для досягнення такої конфігурації знадобиться 50 млрд років[24], що значно перевищує очікуваний термін існування Сонячної системи.

Історія змін орбіти Місяця

[ред. | ред. код]

Лазерні вимірювання свідчать, що середня відстань до Місяця збільшується. Це означає, що в минулому Місяць був ближче до Землі, а тривалість дня на Землі була меншою. Дослідження скам'янілостей молюсків з епохи Кампанського ярусу (80 мільйонів років тому) показують, що в ті часи у земному році було 372 дні, тобто тривалість дня становила 23 години 33 хв. Це означає, що відстань до Місяця становила близько 60,05 радіуса Землі — 383 000 км[20]. Є геологічні підтвердження того, що протягом докембрійської ери (2500 млн рр. тому) середня відстань до Місяця становила близько 52 земних радіуси (332 000 км)[22].

Загальноприйнята Модель ударного формування Місяця стверджує, що Місяць виник внаслідок катастрофічного зіткнення між Землею й іншою планетою, після якого уламки, які утворилися внаслідок потужного удару, зібралися під дією власної гравітації на початковій відстані 3,8 земного радіуса від Землі[25]. Ця теорія передбачає, що зіткнення сталося 4,5 млрд років тому[26].

Історія вимірювань

[ред. | ред. код]

До кінця 1950-х всі розрахунки відстані до Місяця базувалися на оптичних кутових вимірюваннях.

Найдавніше точне вимірювання здійснив Гіппарх у II столітті до н. е. Космічна епоха значно покращила точність наших знань про цю величину. Упродовж 1950-х та 1960-х років проводилися експерименти з використанням радіолокаційних, лазерних, космічних кораблів та комп'ютерного моделювання[27].

Цей розділ має на меті надати ілюстрацію деяких історично значущих або цікавих чимось іншим методів визначення відстані до Місяця, і не претендує на те, щоб бути вичерпним і всеохоплюючим.

Паралакс

[ред. | ред. код]

Найдавніший метод визначення відстані до Місяця передбачав вимірювання кута між Місяцем та обраною опорною точкою з кількох місць одночасно. Синхронізувати час вимірювань можна було, здійснюючи їх у заздалегідь визначений час або під час події, яка спостерігається всіма одночасно. До винаходження точних механічних хронометрів роль події синхронізації зазвичай виконувало місячне затемнення або момент, коли Місяць перетинав певний меридіан (якщо спостерігачі розташовувалися на тій самій довготі). Цю методику вимірювання називають місячний паралакс.

Для підвищення точності необхідно здійснити певні налаштування, як-от регулювання вимірюваного кута для врахування заломлення й спотворення світла, що проходить через атмосферу.

Місячне затемнення

[ред. | ред. код]

Під час ранніх спроб вимірювання відстані до Місяця використовували спостереження за місячними затемненнями, а також знання про величину радіуса Землі та усвідомлення того, що Сонце набагато далі від Землі, ніж Місяць. Спостерігаючи геометрію місячного затемнення, відстань до Місяця можна обчислити за допомогою простих тригонометричних формул.

Найдавнішими свідоцтвами про спроби вимірювання відстані до Місяця за допомогою цієї методики є розрахунки грецького астронома й математика Аристархом Самоського, здійснені у IV ст. до н. е.[28], а пізніше — розрахунки Гіппарха, який визначив, що відстань до Місяця становить 59—67 земних радіусів[29]. Пізніше цей метод зустрічається в роботі Птолемея[30], який отримав результат 64 1/6 у найдальшій точці[31].

Проходження через меридіан

[ред. | ред. код]

Учасники експедиції французького астронома Ендрю Клода де ля Шеруа Кроммеліна спостерігали проходження Місяця через той самий меридіан тієї ж ночі з двох різних місць. Завдяки ретельним вимірюванням 1905—1910 рр. вдалося виміряти кут висоти в той момент, коли конкретний місячний кратер (Mösting A) перетнув місцевий меридіан, зі станції у Гринвічі та на мисі Доброї Надії, які розташовані майже тій самій довготі[32]. Відстань розраховували з похибкою в 30 км. Ця величина залишалася загальноприйнятим значенням відстані до Місяця впродовж наступних 50 років.

Затемнення

[ред. | ред. код]

Фіксуючи момент, коли Місяць покриває фонову зорю (або, аналогічним чином, вимірюючи кут між Місяцем та фоновою зорею в заздалегідь визначений момент), можна визначити відстань до Місяця, якщо вимірювання проводяться з кількох відомих місць, розділених певною відстанню.

У 1952 р. астрономи О'Кіф та Андерсон обчислили відстань до Місяця, спостерігаючи чотири покриття з дев'яти різних локацій[33]. За їхніми розрахунками, середню відстань становить 384 407,6 ± 4,7 км. В 1962 році це значення уточнила Ірен Фішер, яка врахувала оновлені геодезичні дані. Вона отримала значення 384 403,7 ± 2 км[6].

Вимірювання за допомогою радарів

[ред. | ред. код]

У 1957 р. у Військово-морській лабораторії США здійснили експеримент із фіксації відлуння від радіолокаційних сигналів з метою визначити відстань Земля — Місяць. Радіолокаційні імпульси тривалістю 2 мкс транслювалися з 50-футової (15-метрової) радіотарілки. Після того, як радіохвилі відлунилися від поверхні Місяця, було зафіксовано зворотний сигнал і виміряно час затримки. Це давало змогу обчислити подолану відстань. Утім, на практиці співвідношення сигнал/шум виявилося настільки низьким, що здійснити точне вимірювання не вдалося[34].

Експеримент повторили у 1958 році в Королівській радіолокаційній установі в Англії. Радіолокаційні імпульси тривалістю 5 мкс передавалися з піковою потужністю 2 МВт зі швидкістю 260 імпульсів на секунду. Було виявлено зворотний сигнал і виміряно час затримки. Кілька сигналів складали разом, щоб отримати надійний сигнал, накладаючи сліди осцилографа на фотоплівку. Вимірювання дали змогу обчислити відстань із невизначеністю 1,25 км[35].

Ці початкові експерименти мали на меті радше підтвердити концепцію і тривали лише один день. Подальші експерименти тривалістю один місяць дали середнє значення 384 402 ± 1,2 км[36]. Це було найточніше вимірювання відстані до Місяця на той час.

Лазерні вимірювання відстані

[ред. | ред. код]
Експеримент із вимірювання відстані до Місяця за допомогою лазера під час місії «Аполлон-11»

Експеримент, під час якого вимірювалася тривалість польоту лазерних імпульсів, відбитих безпосередньо від поверхні Місяця, здійснили в 1962 році команда Массачусетського технологічного інституту та радянською командою Кримської астрофізичної обсерваторії[37].

Під час місій «Аполлон» в 1969 році космонавти розміщували на поверхні Місяця ретрорефлектори з метою збільшення точності цієї методики. Вимірювання тривають і сьогодні і включають багато лазерних установок. Миттєва точність експериментів із лазерною локацією Місяця здатна забезпечувати точність менше міліметра і є найнадійнішим сучасним методом визначення відстані до Місяця.

Астрономи-любителі та громадські вчені

[ред. | ред. код]

Завдяки сучасній доступності точних пристроїв синхронізації, цифрових фотоапаратів високої роздільної здатності, GPS- приймачів, потужних комп'ютерів та майже миттєвого зв'язку астрономи-любителі набули можливості здійснювати високоточні вимірювання відстані до Місяця власноруч.

23 травня 2007 р. було отримано цифрові фотографії Місяця під час покриття Регулу з двох віддалених локацій, у Греції та Англії. Після вимірювання паралаксу між Місяцем та вибраною фоновою зіркою було розраховано відстань до Місяця[38].

Під час місячного затемнення 15 квітня 2014 року було проведено більш масштабний проект під назвою «Aristarchus Campaign»[16]. Учасникам було запропоновано записати серію з п'яти цифрових фотографій від сходу місяця до кульмінації (точка з найбільшою висотою).

Метод використовує той факт, що Місяць фізично ближче до спостерігача, коли він перебуває у найвищій точці неба, порівняно з тим, коли він перебуває поблизу горизонту. Хоча здається, що Місяць найбільший, коли він знаходиться поблизу горизонту, насправді вірне зворотне. Це явище називають ілюзія Місяця. Його причина полягає в тому, що відстань від центру Місяця до центру Землі майже незмінна протягом всієї ночі, але спостерігач на поверхні Землі насправді перебуває на відстані в один радіус Землі від центру Землі. Цей зсув «наближає» його до Місяця, коли той висить над головою.

Сучасні камери вже досягли такого рівня роздільної здатності, що здатні захопити Місяць із достатньою точністю, щоб виокремити і, що важливіше, виміряти цю крихітну зміну у видимих розмірах. Розрахунки, здійснені в рамках цього експерименту, дали для відстані до Місяця значення 60,51 +3,91 –4,19 земного радіуса. Прийняте значення за ту ніч становило 60,61, що означало 3%-ву точність. Перевага цього методу полягає в тому, що єдиним вимірювальним обладнанням є сучасна цифрова камера (оснащена точним годинником та GPS-приймачем).

Існують також інші експериментальні методи вимірювання відстані до Місяця, доступні астрономам-любителям:

  • Зйомка Місяця перед тим, як він потрапить у півтінь, і після того, як він повністю затьмариться (під час місячного затемнення).
  • Якнайточніше вимірювання моментів контактів під час затемнення.
  • Зйомка якісних зображень часткового затемнення, коли на Місяці добре видно форму й розміри земної тіні.
  • Така зйомка Місяця, щоб у поле зору потрапили Спіка та Марс, — з різних місць.

Див. також

[ред. | ред. код]

Посилання

[ред. | ред. код]
  1. ↑ а б в г д Battat, J. B. R.; Murphy, T. W.; Adelberger, E. G. (January 2009). The Apache Point Observatory Lunar Laser-ranging Operation (APOLLO): Two Years of Millimeter-Precision Measurements of the Earth-Moon Range. Astronomical Society of the Pacific. 121 (875): 29—40. Bibcode:2009PASP..121...29B. doi:10.1086/596748. JSTOR 10.1086/596748.
  2. ↑ а б Murphy, T W (1 липня 2013). Lunar laser ranging: the millimeter challenge (PDF). Reports on Progress in Physics. 76 (7): 2. arXiv:1309.6294. Bibcode:2013RPPh...76g6901M. doi:10.1088/0034-4885/76/7/076901. PMID 23764926. Архів оригіналу (PDF) за 10 квітня 2016. Процитовано 26 липня 2020.
  3. ↑ NEO Earth Close Approaches. Neo.jpl.nasa.gov. Архів оригіналу за 7 березня 2014. Процитовано 22 лютого 2016.
  4. ↑ Williams, J. G.; Newhall, X. X.; Dickey, J. O. (15 червня 1996). Relativity parameters determined from lunar laser ranging (PDF). Physical Review D. 53 (12): 6730—6739. Bibcode:1996PhRvD..53.6730W. doi:10.1103/PhysRevD.53.6730. PMID 10019959. Архів оригіналу (PDF) за 15 жовтня 2006. Процитовано 26 липня 2020.
  5. ↑ Shuch, H. Paul (July 1991). Measuring the mass of the earth: the ultimate moonbounce experiment (PDF). Proceedings, 25th Conference of the Central States VHF Society: 25—30. Архів оригіналу (PDF) за 18 січня 2017. Процитовано 28 лютого 2016.
  6. ↑ а б Fischer, Irene (August 1962). Parallax of the moon in terms of a world geodetic system (PDF). The Astronomical Journal. 67: 373. Bibcode:1962AJ.....67..373F. doi:10.1086/108742. Архів оригіналу (PDF) за 21 травня 2020. Процитовано 26 липня 2020.
  7. ↑ Dickey, J. O.; Bender, P. L. та ін. (22 липня 1994). Lunar Laser Ranging: A Continuing Legacy of the Apollo Program (PDF). Science. 265 (5171): 482—490. Bibcode:1994Sci...265..482D. doi:10.1126/science.265.5171.482. PMID 17781305. Архів оригіналу (PDF) за 4 березня 2016. Процитовано 26 липня 2020.
  8. ↑ Is the Moon moving away from the Earth? When was this discovered? (Intermediate) - Curious About Astronomy? Ask an Astronomer. Curious.astro.cornell.edu. Архів оригіналу за 4 жовтня 2015. Процитовано 22 лютого 2016.
  9. ↑ C.D. Murray & S.F. Dermott (1999). Solar System Dynamics. Cambridge University Press. с. 184.
  10. ↑ Dickinson, Terence (1993). From the Big Bang to Planet X. Camden East, Ontario: Camden House. с. 79–81. ISBN 978-0-921820-71-0.
  11. ↑ Lasater, A. Brian (2007). The dream of the West : the ancient heritage and the European achievement in map-making, navigation and science, 1487–1727. Morrisville: Lulu Enterprises. с. 185. ISBN 978-1-4303-1382-3. Архів оригіналу за 5 серпня 2020. Процитовано 26 липня 2020.
  12. ↑ Leslie, William T. Fox ; illustrated by Clare Walker (1983). At the sea's edge : an introduction to coastal oceanography for the amateur naturalist. Englewood Cliffs, N.J.: Prentice-Hall. с. 101. ISBN 978-0130497833.
  13. ↑ Williams, Dr. David R. (18 листопада 2015). Planetary Fact Sheet - Ratio to Earth Values. NASA Goddard Space Flight Center. Архів оригіналу за 14 травня 2020. Процитовано 28 лютого 2016.
  14. ↑ а б Groten, Erwin (1 квітня 2004). Fundamental Parameters and Current (2004) Best Estimates of the Parameters of Common Relevance to Astronomy, Geodesy, and Geodynamics by Erwin Groten, IPGD, Darmstadt (PDF). Journal of Geodesy. 77 (10–11): 724—797. Bibcode:2004JGeod..77..724.. doi:10.1007/s00190-003-0373-y. Архів оригіналу (PDF) за 11 серпня 2017. Процитовано 2 березня 2016.
  15. ↑ International Astronomical Union | IAU. www.iau.org. Архів оригіналу за 22 жовтня 2009. Процитовано 5 травня 2019.
  16. ↑ а б Zuluaga, Jorge I.; Figueroa, Juan C.; Ferrin, Ignacio (19 травня 2014). The simplest method to measure the geocentric lunar distance: a case of citizen science: (page needed). arXiv:1405.4580. Bibcode:2014arXiv1405.4580Z.
  17. ↑ а б Reasenberg, R.D.; Chandler, J.F. та ін. (2016). Modeling and Analysis of the APOLLO Lunar Laser Ranging Data. arXiv:1608.04758 [astro-ph.IM].
  18. ↑ а б Vitagliano, Aldo (1997). Numerical integration for the real time production of fundamental ephemerides over a wide time span (PDF). Celestial Mechanics and Dynamical Astronomy. 66 (3): 293—308. Bibcode:1996CeMDA..66..293V. doi:10.1007/BF00049383. Архів оригіналу (PDF) за 29 січня 2020. Процитовано 26 липня 2020.
  19. ↑ а б Folkner, W. M.; Williams, J. G. та ін. (February 2014). The Planetary and Lunar Ephemerides DE430 and DE431 (PDF). The Interplanetary Network Progress Report. 42—169. Архів оригіналу (PDF) за 5 березня 2016. Процитовано 26 липня 2020.
  20. ↑ а б Winter, Niels J.; Goderis, Steven; Van Malderen, Stijn J.M. та ін. (18 лютого 2020). Subdaily‐Scale Chemical Variability in a Rudist Shell: Implications for Rudist Paleobiology and the Cretaceous Day‐Night Cycle. Paleoceanography and Paleoclimatology. 35 (2). doi:10.1029/2019PA003723. {{cite journal}}: |access-date= вимагає |url= (довідка)
  21. ↑ Choi, Charles Q. (19 листопада 2014). Moon Facts: Fun Information About the Earth's Moon. Space.com. TechMediaNetworks, Inc. Архів оригіналу за 1 березня 2016. Процитовано 3 березня 2016.
  22. ↑ а б Walker, James C. G.; Zahnle, Kevin J. (17 квітня 1986). Lunar nodal tide and distance to the Moon during the Precambrian (PDF). Nature. 320 (6063): 600—602. Bibcode:1986Natur.320..600W. doi:10.1038/320600a0.
  23. ↑ Bills, B.G. & Ray, R.D. (1999), Lunar Orbital Evolution: A Synthesis of Recent Results, Geophysical Research Letters, 26 (19): 3045—3048, Bibcode:1999GeoRL..26.3045B, doi:10.1029/1999GL008348
  24. ↑ Cain, Fraser (12 квітня 2016). WHEN WILL EARTH LOCK TO THE MOON?. Universe Today. Universe Today. Архів оригіналу за 23 вересня 2016. Процитовано 1 вересня 2016.
  25. ↑ Canup, R. M. (17 жовтня 2012). Forming a Moon with an Earth-like Composition via a Giant Impact. Science. 338 (6110): 1052—1055. Bibcode:2012Sci...338.1052C. doi:10.1126/science.1226073. PMC 6476314. PMID 23076098.
  26. ↑ The Theia Hypothesis: New Evidence Emerges that Earth and Moon Were Once the Same. The Daily Galaxy. 5 липня 2007. Архів оригіналу за 20 лютого 2008. Процитовано 13 листопада 2013.
  27. ↑ Newhall, X.X; Standish, E.M; Williams, J. G. (Aug 1983). DE 102 - A numerically integrated ephemeris of the moon and planets spanning forty-four centuries. Astronomy and Astrophysics. 125 (1): 150—167. Bibcode:1983A&A...125..150N. ISSN 0004-6361. Архів оригіналу за 14 березня 2020. Процитовано 28 лютого 2016.
  28. ↑ Gutzwiller, Martin C. (1998). Moon–Earth–Sun: The oldest three-body problem. Reviews of Modern Physics. 70 (2): 589—639. Bibcode:1998RvMP...70..589G. doi:10.1103/RevModPhys.70.589.
  29. ↑ Sheehan, William; Westfall, John (2004). The transits of Venus. Amherst, N.Y.: Prometheus Books. с. 27—28. ISBN 978-1-59102-175-9. Архів оригіналу за 5 серпня 2020. Процитовано 26 липня 2020.
  30. ↑ Webb, Stephen (1999), 3.2 Aristarchus, Hipparchus, and Ptolemy, Measuring the Universe: The Cosmological Distance Ladder, Springer, с. 27—35, ISBN 978-1-85233-106-1. See in particular p. 33: «Almost everything we know about Hipparchus comes down to us by way of Ptolemy.»
  31. ↑ Helden, Albert van (1986). Measuring the universe : cosmic dimensions from Aristarchus to Halley (вид. Repr.). Chicago: University of Chicago Press. с. 16. ISBN 978-0-226-84882-2.
  32. ↑ Fischer, Irène (7 листопада 2008). The distance of the moon. Bulletin Géodésique. 71 (1): 37—63. Bibcode:1964BGeod..38...37F. doi:10.1007/BF02526081.
  33. ↑ O'Keefe, J. A.; Anderson, J. P. (1952). The earth's equatorial radius and the distance of the moon (PDF). Astronomical Journal. 57: 108—121. Bibcode:1952AJ.....57..108O. doi:10.1086/106720. Архів оригіналу (PDF) за 27 вересня 2021. Процитовано 26 липня 2020.
  34. ↑ Yaplee, B. S.; Roman, N. G.; Scanlan, T. F.; Craig, K. J. (30 July – 6 August 1958). A lunar radar study at 10-cm wavelength. Paris Symposium on Radio Astronomy. IAU Symposium no. 9: 19. Bibcode:1959IAUS....9...19Y.
  35. ↑ Hey, J. S.; Hughes, V. A. (30 July – 6 August 1958). Radar observation of the moon at 10-cm wavelength. Paris Symposium on Radio Astronomy. 9: 13. Bibcode:1959IAUS....9...13H. doi:10.1017/s007418090005049x.
  36. ↑ Yaplee, B. S.; Knowles, S. H. та ін. (January 1965). The mean distance to the Moon as determined by radar. Symposium - International Astronomical Union. 21: 2. Bibcode:1965IAUS...21...81Y. doi:10.1017/S0074180900104826.
  37. ↑ Bender, P. L.; Currie, D. G.; Dicke, R. H. та ін. (19 жовтня 1973). The Lunar Laser Ranging Experiment (PDF). Science. 182 (4109): 229—238. Bibcode:1973Sci...182..229B. doi:10.1126/science.182.4109.229. PMID 17749298. Архів оригіналу (PDF) за 15 лютого 2017. Процитовано 27 квітня 2013.
  38. ↑ Wright, Ernie. Overhead view of the Earth-Moon system, to scale Lunar Parallax: Estimating the Moon's Distance. Архів оригіналу за 7 березня 2016. Процитовано 29 лютого 2016.

Посилання

[ред. | ред. код]
Отримано з https://uk.wikipedia.org/w/index.php?title=Відстань_до_Місяця&oldid=39367179