Баєсова мережа
| Ця стаття містить перелік посилань, але походження окремих тверджень залишається незрозумілим через брак внутрішньотекстових джерел-виносок. (грудень 2016) |
Ба́єсова мере́жа, мере́жа Ба́єса, мере́жа перекона́нь, ба́єсова моде́ль або ймові́рнісна орієнто́вана ациклі́чна гра́фова моде́ль (англ. Bayesian network, Bayes network, belief network, Bayes(ian) model, probabilistic directed acyclic graphical model) — це ймовірнісна графова модель (різновид статистичної моделі), яка представляє набір випадкових змінних та їхніх умовних залежностей[en] за допомогою орієнтованого ациклічного графу (ОАГ, англ. directed acyclic graph, DAG). Наприклад, баєсова мережа може представляти ймовірнісні зв'язки між захворюваннями та симптомами. Таку мережу можна використовувати для обчислення ймовірностей наявності різних захворювань за наявних симптомів.
Формально баєсові мережі є ОАГ, чиї вершини представляють випадкові змінні у баєсовому сенсі: вони можуть бути спостережуваними величинами, латентними змінними, невідомими параметрами або гіпотезами. Ребра представляють умовні залежності; не з'єднані вершини (такі, що в Баєсовій мережі не існує шляху від однієї змінної до іншої) представляють змінні, що є умовно незалежними[en] одна від одної. Кожну вершину пов'язано із функцією ймовірності, що бере на вході певний набір значень батьківських вершин, і видає (на виході) ймовірність (або розподіл імовірності, якщо застосовно) змінної, представленої цією вершиною. Наприклад, якщо батьківських вершин представляють булевих змінних, то функцію ймовірності може бути представлено таблицею записів, по одному запису для кожної з можливих комбінацій істинності або хибності її батьків. Схожі ідеї можуть застосовуватися до неорієнтованих та, можливо, циклічних графів, таких як марковські мережі.
Існують ефективні алгоритми, що виконують висновування та навчання в баєсових мережах. Баєсові мережі, що моделюють послідовності змінних (наприклад, сигнали мовлення, або послідовності білків), називають динамічними баєсовими мережами. Узагальнення баєсових мереж, що можуть представляти та розв'язувати задачі ухвалення рішень за умов невизначеності, називають діаграмами впливу[en].
Приклад[ред. | ред. код]

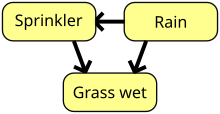
Припустімо, що існують дві події, які можуть спричинити мокрість трави: або увімкнено розбризкувач, або йде дощ. Також припустімо, що дощ має прямий вплив на використання розбризкувача (а саме, коли йде дощ, розбризкувач зазвичай не увімкнено). Тоді цю ситуацію може бути змодельовано баєсовою мережею (показаною праворуч). Всі три змінні мають два можливі значення, T (істина, англ. True) та F (хиба, англ. False).
Функцією спільного розподілу ймовірності є
де назви змінних є скороченнями G = трава мокра (англ. Grass wet, так/ні), S = розбризкувач увімкнено (англ. Sprinkler, так/ні) та R = іде дощ (англ. Raining, так/ні).
Ця модель може відповідати на такі питання, як «Якою є ймовірність того, що йде дощ, якщо трава мокра?» шляхом застосування формули умовної ймовірності та підбиття сум за всіма завадними змінними[en]:
Використовуючи розклад спільної функції ймовірності , та умовні ймовірності з таблиць умовної ймовірності[en], зазначених у діаграмі, можна оцінити кожен член у сумах чисельника та знаменника. Наприклад,
Тоді числовими результатами (з пов'язаними значеннями змінних в індексах) є
З іншого боку, якщо ми хочемо відповісти на втручальницьке питання «Яка ймовірність того, що піде дощ, якщо ми намочимо траву?», то відповідь визначатиметься післявтручальною функцією спільного розподілу , отриманою усуненням коефіцієнту із довтручального розподілу. Як і очікувалося, на ймовірність дощу ця дія не впливає: .
Понад те, якщо ми хочемо передбачити вплив умикання розбризкувача, то ми маємо
з усуненим членом , що показує, що ця дія має вплив на траву, але не на дощ.
Ці передбачення не можуть бути здійсненними, якщо якісь змінні є неспостережуваними, як у більшості задач оцінки стратегій. Вплив дії все ще можна передбачувати, проте лише якщо задовольняється критерій «чорного ходу».[1][2] Він заявляє, що якщо може спостерігатися множина вузлів Z, яка о-розділює[3] (або блокує) всі чорні ходи (англ. back-door paths) з X до Y, то . Чорний хід є таким, що закінчується стрілкою в X. Множини, які задовольняють критерій чорного ходу, називають «достатніми» (англ. sufficient) або «прийнятними» (англ. admissible). Наприклад, множина Z = R є прийнятною для передбачування впливу S = T на G, оскільки R о-розділює (єдиний) чорний хід S ← R → G. Проте якщо S не спостерігається, то не існує іншої множини, яка би о-розділювала цей шлях, і вплив умикання розбризкувача (S = T) на траву (G) не може бути передбачено з пасивних спостережень. Тоді ми кажемо, що множина P(G | do(S = T)) є не пізннаною (англ. not identified). Це віддзеркалює той факт, що за умови браку даних втручання ми не можемо визначити, чи завдячує спостережувана залежність між S та G випадковому зв'язкові або є фальшивою (видима залежність, що випливає зі спільної причини, R). (див. парадокс Сімпсона)
Для з'ясування того, чи є причинний зв'язок пізнанним із довільної баєсової мережі з неспостережуваними змінними, можна застосовувати три правила числення дій (англ. do-calculus),[1][4] і перевіряти, чи всі do-члени може бути усунено з виразу для цього співвідношення, підтверджуючи таким чином, що бажана величина є оцінкою із частотних даних.[5]
Застосування баєсової мережі може заощаджувати значні обсяги пам'яті, якщо залежності в спільному розподілі є розрідженими. Наприклад, наївний спосіб зберігання умовних імовірностей для 10 двозначних змінних як таблиці вимагає простору для зберігання значень. Якщо локальні розподіли жодної зі змінних не залежать більше ніж від трьох батьківських змінних, то представлення як баєсової мережі потребує зберігання щонайбільше значень.
Однією з переваг баєсових мереж є те, що людині інтуїтивно простіше розуміти (розріджені набори) прямих залежностей та локальні розподіли, ніж повні спільні розподіли.
Висновування та навчання[ред. | ред. код]
Для баєсових мереж існує три основні завдання для висновування.
Отримування висновків про неспостережувані змінні[ред. | ред. код]
Оскільки баєсова мережа є повною моделлю змінних та їхніх взаємозв'язків, її можна використовувати для отримання відповідей на ймовірнісні запити стосовно них. Наприклад, цю мережу можна використовувати для з'ясовування уточненого знання про стан якоїсь підмножини змінних, коли спостерігаються інші змінні (змінні свідчення, англ. evidence). Цей процес обчислення апостеріорного розподілу змінних для заданого свідчення називається ймовірнісним висновуванням (англ. probabilistic inference). Це апостеріорне дає універсальну достатню статистику для застосувань для виявлення, коли потрібно підбирати значення підмножини змінних, які мінімізують певну функцію очікуваних втрат, наприклад, імовірність помилковості рішення. Баєсову мережу відтак можна розглядати як механізм автоматичного застосування теореми Баєса до комплексних задач.
Найпоширенішими методами точного висновування є: виключення змінних[en], яке виключає (інтегруванням або підсумовуванням) неспостережувані не запитові змінні одну по одній шляхом розподілу суми над добутком; поширення деревом злук[en], яке кешує обчислення таким чином, що одночасно можна робити запит до багатьох змінних, а нові свідчення можуть поширюватися швидко; та рекурсивне обумовлювання й пошук ТА/АБО, які передбачають просторово-часовий компроміс та підбирають ефективність виключення змінних при використанні достатнього простору. Всі ці методи мають експоненційну складність відносно деревної ширини мережі. Найпоширенішими алгоритмами наближеного висновування[en] є вибірка за значимістю, стохастична імітація МКМЛ, міні-блокове виключення (англ. mini-bucket elimination), петельне поширення переконання[en], поширення узагальненого переконання[en] та варіаційні методи[en].
Навчання параметрів[ред. | ред. код]
Щоби повністю описати баєсову мережу, і відтак повністю представити спільний розподіл імовірності, необхідно для кожного вузла X вказати розподіл імовірності X, обумовлений батьками X. Цей розподіл X, обумовлений батьками X, може мати будь-який вигляд. Є звичним працювати з дискретними або ґаусовими розподілами, оскільки це спрощує обчислення. Іноді відомі лише обмеження на розподіл; тоді можна застосовувати принцип максимальної ентропії[en] для визначення єдиного розподілу, який має найбільшу ентропію для заданих обмежень. (Аналогічно, в конкретному контексті динамічних баєсових мереж зазвичай вказують такий умовний розподіл розвитку в часі прихованих станів, щоби максимізувати ентропійну швидкість цього неявного стохастичного процесу.)
Ці умовні розподіли часто включають параметри, які є невідомими, і мусять бути оцінені з даних, іноді із застосуванням підходу максимальної правдоподібності. Пряма максимізація правдоподібності (або апостеріорної ймовірності) часто є складною, коли є неспостережувані змінні. Класичним підходом до цієї задачі є алгоритм очікування-максимізації, який чередує обчислення очікуваних значень неспостережених змінних за умови спостережуваних даних із максимізацією повної правдоподібності (або апостеріорного), виходячи з припущення про правильність попередньо обчислених очікуваних значень. За м'яких умов закономірності цей процес збігається до значень параметрів, які дають максимальну правдоподібність (або максимальне апостеріорне).
Повнішим баєсовим підходом до параметрів є розгляд параметрів як додаткових неспостережуваних змінних і обчислення повного апостеріорного розподілу над усіма вузлами за умови спостережуваних даних, із наступним відінтегровуванням параметрів. Цей підхід може бути витратним і вести до моделей великої розмірності, тому на практиці поширенішими є класичні підходи встановлення параметрів.
Навчання структури[ред. | ред. код]
У найпростішому випадку баєсова мережа задається фахівцем, і потім застосовується для виконання висновування. В інших застосуваннях задача визначення цієї мережі є занадто складною для людей. В такому випадку структури мережі та параметрів локальних розподілів треба навчатися з даних.
Автоматичне навчання структури баєсової мережі є проблемою, якою займається машинне навчання. Основна ідея сходить до алгоритму виявлення, розробленого Ребане та Перлом 1987 року,[6] який спирається на розрізнення між трьома можливими типами суміжних трійок, дозволеними в орієнтованому ациклічному графі (ОАГ):
Типи 2 та 3 представляють однакові залежності ( та є незалежними за заданого ), і, відтак, є нерозрізнюваними. Проте тип 3 може бути унікально виявлено, оскільки та є відособлено незалежними, а всі інші пари є залежними. Таким чином, в той час як кістяки (англ. skeletons, графи із зачищеними стрілками) цих трьох трійок є однаковими, напрямок стрілок частково підлягає виявленню. Таке саме розрізнення застосовується й тоді, коли та мають спільних батьків, тільки спочатку треба зробити обумовлення за цими батьками. Було розроблено алгоритми для систематичного визначення кістяка графу, що лежить в основі, а потім спрямовуванні всіх стрілок, чия спрямованість диктується спостережуваними умовними незалежностями.[1][7][8][9]
Альтернативний метод навчання структури застосовує пошук на основі оптимізації. Він потребує оцінкової функції[en] та стратегії пошуку. Поширеною оцінковою функцією є апостеріорна ймовірність структури за заданих тренувальних даних, така як БІК або BDeu. Часові вимоги вичерпного пошуку, що повертає структуру, яка максимізує оцінку, є суперекспонентними відносно числа змінних. Стратегія локального пошуку робить поступові зміни, спрямовані на поліпшення оцінки структури. Алгоритм глобального пошуку, такий як метод Монте-Карло марковських ланцюгів, може уникати потрапляння в пастку локального мінімуму. Фрідман та ін.[10][11] обговорюють застосування взаємної інформації між змінними, та пошуку структури, яка її максимізує. Вони роблять це шляхом обмеження набору кандидатів у батьки k вузлами, і вичерпним пошуком серед таких.
Особливо швидким методом точного навчання БМ є розгляд цієї задачі як задачі оптимізації, й розв'язання її із застосуванням цілочисельного програмування. Обмеження ациклічності додаються цілочисельній програмі під час розв'язання у вигляді січних площин[en].[12] Такий метод може впоруватися із задачами, що мають до 100 змінних.
Щоби мати справу із задачами з тисячами змінних, необхідно застосовувати інший підхід. Одним з них є спочатку вибирати одне впорядкування, і потім знаходити оптимальну структуру БМ по відношенню до цього впорядкування. Це означає роботу на просторі пошуку можливих впорядкувань, що є зручним, оскільки він менший за простір мережних структур. Потім вибираються й оцінюються декілька впорядкувань. Було доведено, що цей метод є найкращим із доступних в наукових працях, коли число змінних є величезним.[13]
Інший метод полягає в зосередженні на підкласах розкладаних моделей, для яких оцінка максимальної правдоподібності має замкнений вигляд. Тоді можливо виявляти цілісну структуру для сотень змінних.[14]
Баєсова мережа може доповнюватися вузлами та ребрами із застосуванням методик машинного навчання на основі правил. Для добування правил та створення нових вузлів може застосовуватися індуктивне логічне програмування[en].[15] Підходи статистичного навчання відношень[en] (СНВ, англ. statistical relational learning, SRL) використовують оцінкову функцію[en], що ґрунтується на структурі баєсової мережі, для спрямовування структурного пошуку та доповнення мережі.[16] Поширеною оцінковою функцією СНВ є площа під кривою РХП.
Як зазначено раніше, навчання баєсових мереж із обмеженою деревною шириною є необхідним для уможливлення точного розв'язного висновування, оскільки складність висновування в найгіршому випадку є експонентною по відношенню до деревної ширини k (за гіпотези експонентного часу). Проте, будучи глобальною властивістю графу, вона значно підвищує складність процесу навчання. В цьому контексті для ефективного навчання можливо застосовувати поняття k-дерева.[17]
Статистичне введення[ред. | ред. код]
Для заданих даних та параметру простий баєсів аналіз починається з апріорної ймовірності (апріорного) та правдоподібності для обчислення апостеріорної ймовірності .
Часто апріорне залежить у свою чергу від інших параметрів , які не згадуються в правдоподібності. Отже, апріорне мусить бути замінено правдоподібністю , і потрібним апріорним нововведених параметрів , що дає в результаті апостеріорну ймовірність
Це є найпростішим прикладом ієрархічної баєсової моделі (англ. hierarchical Bayes model).[прояснити: <span style="border-bottom:1px dotted; cursor:help;" title='Що робить її ієрархічною? Ми говоримо про ієрархія (математика)[en], чи ієрархічна структура? Поставте посилання на відповідне. (грудень 2016)'>ком.]
Цей процес може повторюватися; наприклад, параметри можуть у свою чергу залежати від додаткових параметрів , які потребуватимуть свого власного апріорного. Зрештою цей процес мусить завершитися апріорними, які не залежать від жодних інших незгаданих параметрів.
Ввідні приклади[ред. | ред. код]
| Цей розділ потребує доповнення. (грудень 2016) |
Припустімо, що ми виміряли величини , кожна із нормально розподіленою похибкою відомого стандартного відхилення ,
Припустімо, що нас цікавить оцінка . Підходом буде оцінювати із застосуванням методу максимальної правдоподібності; оскільки спостереження є незалежними, правдоподібність розкладається на множники, і оцінкою максимальної правдоподібності є просто
Проте, якщо ці величини є взаємопов'язаними, так що, наприклад, ми можемо думати, що окремі було й самі вибрано з розподілу, що лежав в основі, то цей взаємозв'язок руйнує незалежність, і пропонує складнішу модель, наприклад,
з некоректними апріорними flat, flat. При це є пізнанною моделлю (тобто, існує унікальний розв'язок для параметрів моделі), а апостеріорні розподіли окремих будуть схильні рухатися, або стискатися[en] (англ. shrink) від оцінок максимальної правдоподібності до свого спільного середнього. Це стискання (англ. shrinkage) є типовою поведінкою ієрархічних баєсових моделей.
Обмеження на апріорні[ред. | ред. код]
При виборі апріорних в ієрархічній моделі потрібна деяка обережність, зокрема на масштабних змінних на вищих рівнях ієрархії, таких як змінна у цьому прикладі. Звичайні апріорні, такі як апріорне Джеффріса[en], часто не працюють, оскільки апостеріорний розподіл буде некоректним (його неможливо буде унормувати), а оцінки, зроблені мінімізуванням очікуваних втрат будуть неприйнятними[en].
Визначення та поняття[ред. | ред. код]
Існує декілька рівнозначних визначень баєсової мережі. Для всіх наступних, нехай G = (V,E) є орієнтованим ациклічним графом (або ОАГ), і нехай X = (Xv)v ∈ V є множиною випадкових змінних, проіндексованою за V.
Множникове визначення[ред. | ред. код]
X є баєсовою мережею по відношенню до G, якщо функцію її спільної густини ймовірності (по відношенню до добуткової міри) може бути записано як добуток окремих функцій густини, обумовлених їхніми батьківськими змінними:[18]
де pa(v) є множиною батьків v (тобто, тих вершин, які вказують безпосередньо на v через єдине ребро).
Для будь-якої множини випадкових змінних імовірність будь-якого члену спільного розподілу може бути обчислено з умовних імовірностей із застосуванням ланцюгового правила (для заданого топологічного впорядкування X) наступним чином:[18]
Порівняйте це із наведеним вище визначенням, що його може бути записано наступним чином:
- для кожного що є батьком
Різницею між цими двома виразами є умовна незалежність[en] змінних від будь-якого з їхніх не-нащадків за заданих значень їхніх батьківських змінних.
Локальна марковська властивість[ред. | ред. код]
X є баєсовою мережею по відношенню до G, якщо вона задовольняє локальну марковську властивість (англ. local Markov property): кожна змінна є умовно незалежною[en] від своїх не-нащадків за заданих її батьківських змінних:[19]
- для всіх
де de(v) є множиною нащадків, а V \ de(v) є множиною не-нащадків v.
Це також може бути виражено в подібних до першого визначення термінах як
- для кожного що не є нащадком для кожного що є батьківським для
Зауважте, що множина батьків є підмножиною множини не-нащадків, оскільки граф є ациклічним.
Розробка баєсових мереж[ред. | ред. код]
Для розробки баєсових мереж ми часто спочатку розробляємо такий ОАГ G, що ми переконані, що X задовольняє локальну марковську властивість по відношенню до G. Іноді це робиться шляхом створення причинного[en] ОАГ. Потім ми з'ясовуємо умовні розподіли ймовірності для кожної змінної за заданих її батьків у G. В багатьох випадках, зокрема, в тому випадку, коли змінні є дискретними, якщо ми визначаємо спільний розподіл X як добуток цих умовних розподілів, то X є баєсовою мережею по відношенню до G.[20]
Марковське покриття[ред. | ред. код]
Марковське покриття вузла є множиною вузлів, яка складається з його батьківських вузлів, його дочірніх вузлів, та всіх іншиї батьків його дочірніх вузлів. Марковське покриття робить вузол незалежним від решти мережі; спільний розподіл змінних у марковському покритті вузла є достатнім знанням для обчислення розподілу цього вузла. X є баєсовою мережею по відношенню до G, якщо кожен вузол є умовно незалежним від всіх інших вузлів мережі за заданого його марковського покриття.[19]
о-розділеність[ред. | ред. код]
Це визначення можна зробити загальнішим через визначення о-розділеності (англ. d-separation) двох вузлів, де «о» значить «орієнтована» (англ. directional).[21][22] Нехай P є ланцюгом від вузла u до v. Ланцюг — це ациклічний неорієнтований шлях між двома вузлами (тобто, напрям ребер при побудові цього шляху ігнорується), в якому ребра можуть мати будь-який напрям. Тоді про P кажуть, що він о-розділюється множиною вузлів Z, якщо виконуються будь-які з наступних умов:
- P містить орієнтований шлях, або , такий, що середній вузол m належить Z,
- P містить розгалуження, , таке, що середній вузол m належить Z, або
- P містить обернене розгалуження (або колайдер), , таке, що середній вузол m не належить Z, і жодні з нащадків m не належать Z
X є баєсовою мережею по відношенню до G, якщо для будь-яких двох вузлів u та v
де Z є множиною, яка о-розділює u та v. (Марковське покриття є мінімальним набором вузлів, які о-відділюють вузол v від решти вузлів.)
Ієрархічні моделі[ред. | ред. код]
Термін ієрархічна модель (англ. hierarchical model) іноді вважається окремим типом басової мережі, але він не має формального визначення. Іноді цей термін резервують для моделей з трьома або більше шарами випадкових змінних; в інших випадках його резервують для моделей із латентними змінними. Проте в цілому «ієрархічною» зазвичай називають будь-яку помірно складну баєсову мережу.
Причинні мережі[ред. | ред. код]
Хоч баєсові мережі й використовують часто для представлення причинних взаємозв'язків, це не обов'язково повинно бути так: орієнтоване ребро з u до v не вимагає, щоби Xv причинно залежало від Xu. Про це свідчить той факт, що баєсові мережі на графах
- та
є рівнозначними: тобто, вони накладають точно такі ж вимоги умовної незалежності.
Причи́нна мере́жа (англ. causal network) — це баєсова мережа з явною вимогою того, що взаємозв'язки є причинними. Додаткова семантика причинних мереж вказує, що якщо вузлові X активно спричинено перебування в заданому стані x (дія, що записується як do(X = x)), то функція густини ймовірності змінюється на функцію густини ймовірності мережі, отриманої відсіканням з'єднань від батьків X до X, і встановленням X у спричинене значення x.[1] Застосовуючи ці семантики, можна передбачувати вплив зовнішніх втручань на основі даних, отриманих до втручання.
Складність висновування та алгоритми наближення[ред. | ред. код]
1990 року під час праці в Стенфордському університеті над великими застосунками в біоінформатиці Грег Купер довів, що точне висновування в баєсових мережах є NP-складним.[23] Цей результат спричинив сплеск досліджень алгоритмів наближення з метою розробки розв'язного наближення ймовірнісного висновування. 1993 року Пол Деґам та Майкл Любі довели два несподівані результати стосовно складності наближення ймовірнісного висновування в баєсових мережах.[24] По-перше, вони довели, що не існує розв'язного детермінованого алгоритму, який міг би наближувати ймовірнісне висновування в межах абсолютної похибки ɛ< 1/2. По-друге, вони довели, що не існує розв'язного увипадковленого алгоритму, який міг би наближувати ймовірнісне висновування в межах абсолютної похибки ɛ < 1/2 з довірчою ймовірністю понад 1/2.
Приблизно в той же час Ден Рот[en] довів, що точне висновування в баєсових мережах фактично є #P-повним[en] (і відтак настільки ж складним, як і підрахунок числа задовільних присвоєнь КНФ-формули), і що наближене висновування, навіть для баєсових мереж із обмеженою архітектурою, є NP-складним.[25][26]
З практичної точки зору, ці результати стосовно складності підказали, що хоча баєсові мережі й були цінними представленнями для застосунків ШІ та машинного навчання, їхнє застосування у великих реальних задачах вимагатиме пом'якшення або топологічними структурними обмеженнями, такими як наївні баєсові мережі, або обмеженнями на умовні ймовірності. Алгоритм обмеженої дисперсії (англ. bounded variance algorithm)[27] був першим алгоритмом довідного швидкого наближення для ефективного наближення ймовірнісного висновування в баєсових мережах з гарантією похибки наближення. Цей потужний алгоритм вимагав другорядних обмежень умовних імовірностей баєсової мережі, щоби отримати відмежування від нуля та одиниці на 1/p(n), де p(n) є будь-яким поліномом від числа вузлів мережі n.
Застосування[ред. | ред. код]
Баєсові мережі застосовують для моделювання переконань в обчислювальній біології та біоінформатиці (аналізі генних регуляторних мереж, структур білків, експресії генів,[28] навчанні епістазів із наборів даних GWAS[en][29]), медицині,[30] біомоніторингу[en],[31] класифікації документів, інформаційному пошуку,[32] семантичному пошуку[en],[33] обробці зображень, злитті даних, системах підтримки ухвалення рішень,[34] інженерії, ставках на спорт,[35][36] іграх, праві,[37][38][39] розробці досліджень[40] та аналізі ризиків.[41] Існують праці про застосування баєсових мереж в біоінформатиці[42][43] та фінансовій і маркетинговій інформатиці.[44][45]
Програмне забезпечення[ред. | ред. код]
- libDAI [Архівовано 14 червня 2017 у Wayback Machine.] Вільна відкрита бібліотека C++ дискретного наближеного висновування (англ. Discrete Approximate Inference) в графових моделях. libDAI підтримує такі методи висновування як точне висновування перебором грубою силою, точне висновування методами дерева злук[en], осередненого поля[en], петельного поширення переконання[en], вибірки за Ґіббсом[en], обумовленого поширення переконання (англ. Conditioned Belief Propagation) та деякі інші.
- Mocapy++ [Архівовано 21 грудня 2016 у Wayback Machine.] Інструментарій динамічних баєсових мереж, реалізований мовою C++. Він підтримує дискретні, багаточленні, ґаусові, кентові, фон мізесові та пуассонові вузли. Висновування та навчання здійснюються вибіркою за Ґіббсом/стохастичним очікуванням-максимізацією.
- WinBUGS[en] Одна з перших обчислювальних реалізацій вибірок МКМЛ. Більше не підтримується й не рекомендується для активного застосування.
- OpenBUGS[en] (сайт [Архівовано 9 липня 2016 у Wayback Machine.]), подальша (відкрита) розробка WinBUGS.
- Just another Gibbs sampler[en] (JAGS) (сайт) Інша відкрита альтернатива WinBUGS. Використовує вибірку за Ґіббсом.
- Stan (програмне забезпечення)[en] (сайт [Архівовано 3 вересня 2012 у Wayback Machine.]) Відкритий пакет для отримування баєсового висновування із застосуванням безрозворотної вибірки (англ. No-U-Turn sampler), одного з варіантів гамільтонового Монте-Карло[en]. Він в чомусь подібний до BUGS, але з іншою мовою для вираження моделей та іншою вибіркою для відбору зразків з їхніх апостеріорних. RStan це інтерфейс R до Stan. Його підтримують Андрій Гельман[en] з колегами.
- Direct Graphical Models [Архівовано 22 грудня 2016 у Wayback Machine.] (DGM) — відкрита бібліотека C++, яка реалізує різні завдання в імовірнісних графових моделях із попарними залежностями.
- OpenMarkov [Архівовано 25 листопада 2016 у Wayback Machine.] — відкрите програмне забезпечення та ППІ, реалізовані в Java
- Graphical Models Toolkit (GMTK) — відкритий загальнодоступний інструментарій для швидкого прототипування статистичних моделей із застосуванням динамічних графових моделей (ДГМ, англ. dynamic graphical models, DGM) і динамічних баєсових мереж (ДБМ, англ. dynamic Bayesian networks, DBN). GMTK можливо застосовувати для застосунків та досліджень в обробці мовлення та мови, в біоінформатиці, розпізнаванні діяльності[en] та будь-яких застосунках часових рядів.
- PyMC [Архівовано 4 грудня 2016 у Wayback Machine.] — модуль Python, який реалізує баєсові статистичні моделі та алгоритми допасовування, включно з Монте-Карло марковських ланцюгів. Його гнучкість та розширюваність роблять його застосовним для великого набору задач. Поряд із ядровою функційністю вибірки, PyMC включає методи підсумовування виходу, графічного представлення, а також діагностування якості допасовування та збіжності.
- GeNIe&Smile [Архівовано 1 квітня 2022 у Wayback Machine.] — SMILE це бібліотека C++ для баєсових мереж та діаграм впливу, а GeNIe це ГІК для неї
- SamIam [Архівовано 22 листопада 2016 у Wayback Machine.] — система на основі Java з ГІК та ППІ Java
- Bayes Server [Архівовано 8 квітня 2022 у Wayback Machine.] — користувацький інтерфейс та ППІ для баєсових мереж, включає підтримку часових рядів та послідовностей
- Blip — вебінтерфейс, який пропонує структурне навчання баєсових мереж безпосередньо з дискретних даних. Він може обробляти набори даних із тисячами змінних, і пропонує і пропонує як необмежене, так і обмежене деревною шириною навчання структури.
- Belief and Decision Networks на AIspace [Архівовано 20 грудня 2016 у Wayback Machine.]
- BayesiaLab [Архівовано 20 грудня 2016 у Wayback Machine.] від Bayesia
- Hugin [Архівовано 30 травня 2020 у Wayback Machine.]
- AgenaRisk [Архівовано 9 березня 2022 у Wayback Machine.]
- Netica [Архівовано 4 грудня 2016 у Wayback Machine.] від Norsys
- Bayesian network application library [Архівовано 11 червня 2007 у Wayback Machine.]
- dVelox від Apara Software
- System Modeler від Inatas AB
- UnBBayes [Архівовано 21 грудня 2016 у Wayback Machine.] від GIA-UnB (Intelligence Artificial Group — University of Brasilia)
- [1] [Архівовано 12 жовтня 2016 у Wayback Machine.] із застосуванням технології новітнього аналізу лицьової дисморфології (англ. Facial Dysmorphology Novel Analysis, FDNA)
- Uninet [Архівовано 4 січня 2017 у Wayback Machine.] — неперервні баєсові мережі, які моделюють неперервні змінні, з широким спектром параметричних та непараметричних відособлених розподілів, і залежністю з паруванням. Також підтримуються гібридні дискретно-неперервні моделі. Безкоштовне для некомерційного використання. Розроблено компанією LightTwist Software.
- Tetrad [Архівовано 4 січня 2017 у Wayback Machine.] — відкритий проект, написаний на Java, та розроблений Факультетом філософії університету Карнегі-Меллон, який займається причинними моделями та статистичними даними.
- Dezide [Архівовано 8 березня 2022 у Wayback Machine.]
- bnlearn [Архівовано 2 травня 2022 у Wayback Machine.] — пакет R
- RISO [Архівовано 4 березня 2007 у Wayback Machine.] (розподілені мережі переконань)
- BANSY3 [Архівовано 20 липня 2011 у Wayback Machine.] — Безкоштовне. Від the Non Linear Dynamics Laboratory. Mathematics Department, Science School, UNAM.
- MSBNx [Архівовано 11 жовтня 2008 у Wayback Machine.] — компонентно-орієнтований інструментарій для моделювання та висновування з баєсовими мережами (від Microsoft Research)
- Bayes Net Toolbox [Архівовано 4 січня 2017 у Wayback Machine.] для Matlab
Історія[ред. | ред. код]
Термін «баєсові мережі» (англ. Bayesian networks) було запроваджено Йудою Перлом 1985 року для підкреслення трьох аспектів:[46]
- Часто суб'єктивної природи вхідної інформації.
- Покладання на баєсове обумовлювання як основу для уточнення інформації.
- Відмінності причинної та доказової моделей міркування, яка підкреслює працю Томаса Баєса, опубліковану посмертно 1763 року.[47]
Наприкінці 1980-х років праці Йуди Перла «Імовірнісне міркування в інтелектуальних системах»[48] та Річарда Неаполітана «Імовірнісне міркування в експертних системах»[49] підсумували властивості баєсових мереж та утвердили баєсові мережі як область дослідження.
Неофіційні варіанти таких мереж було вперше застосовано 1913 року юристом Джоном Генрі Вігмором у вигляді діаграм Вігмора[en] для аналізу процесуальних доказів.[38] Інший варіант, що називається діаграмами шляхів[en], було розроблено генетиком Сьюелом Райтом[en],[50] і застосовано в суспільній та поведінковій науці (переважно в лінійних параметричних моделях).
В своїй книзі 2018 року «Книга про Чому» Перл зізнався, що хоч і признає їх успішність в цілому, баєсові мережі не виправдали його сподівань (наблизити машинний інтелект до людського). Він також пояснив чому: мережі виводили висновки через спостережені ймовірності, але не враховували причинність. Думка про ймовірну помилковість конструкції баєсових мереж виникла у нього одразу ж після публікації книги «Імовірнісне міркування в інтелектуальних системах»[51], що і призвело до появи причинних мереж[1].
Див. також[ред. | ред. код]
- Алгоритм очікування-максимізації
- Аналіз шляхів[en]
- Баєсова ймовірність
- Баєсова мережа змінного порядку[en]
- Баєсове висновування
- Баєсове програмування
- Вирівнювання послідовностей
- Глибока мережа переконань
- Граф розкладу[en]
- Графова модель
- Дерево Чоу — Лю[en]
- Динамічна баєсова мережа
- Діаграма Вігмора[en]
- Діаграма впливу[en]
- Ієрархічна часова пам'ять
- Джуда Перл
- Злиття давачів
- Машинне навчання
- Моделювання структурними рівняннями[en]
- Наївний баєсів класифікатор
- Обчислювальна філогенетика[en]
- Обчислювальний інтелект
- Полідерево[en]
- Поширення переконання[en]
- Причинно-петльова діаграма[en]
- Розпізнавання мовлення
- Світогляд
- Система пам'яті—передбачування
- Суб'єктивна логіка[en]
- Сумішева модель[en]
- Сумішевий розподіл
- Теорема Баєса
- Теорія Демпстера — Шафера[en] — узагальнення теореми Баєса
- Фільтр Калмана
- Штучний інтелект
Примітки[ред. | ред. код]
- ↑ а б в г д Pearl, Judea (2000). Causality: Models, Reasoning, and Inference. Cambridge University Press. ISBN 0-521-77362-8. OCLC 42291253. (англ.)
- ↑ The Back-Door Criterion (PDF). Архів оригіналу (PDF) за 27 грудня 2013. Процитовано 18 вересня 2014. (англ.)
- ↑ d-Separation without Tears (PDF). Архів оригіналу (PDF) за 4 березня 2016. Процитовано 18 вересня 2014. (англ.)
- ↑ J., Pearl (1994). A Probabilistic Calculus of Actions. У Lopez de Mantaras, R.; Poole, D. (ред.). UAI'94 Proceedings of the Tenth international conference on Uncertainty in artificial intelligence. San Mateo CA: Morgan Kaufman. с. 454—462. arXiv:1302.6835. ISBN 1-55860-332-8. (англ.)
- ↑ I. Shpitser, J. Pearl, «Identification of Conditional Interventional Distributions» In R. Dechter and T.S. Richardson (Eds.), Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence, 437—444, Corvallis, OR: AUAI Press, 2006. (англ.)
- ↑ Rebane, G. and Pearl, J., "The Recovery of Causal Poly-trees from Statistical Data, " Proceedings, 3rd Workshop on Uncertainty in AI, (Seattle, WA) pages 222—228, 1987 (англ.)
- ↑ Spirtes, P.; Glymour, C. (1991). An algorithm for fast recovery of sparse causal graphs. Social Science Computer Review. 9 (1): 62—72. doi:10.1177/089443939100900106. Архів оригіналу (PDF) за 16 квітня 2016. Процитовано 9 грудня 2016. (англ.)
- ↑ Spirtes, Peter; Glymour, Clark N.; Scheines, Richard (1993). Causation, Prediction, and Search (вид. 1st). Springer-Verlag. ISBN 978-0-387-97979-3. Архів оригіналу за 7 лютого 2017. Процитовано 9 грудня 2016. (англ.)
- ↑ Verma, Thomas; Pearl, Judea (1991). Equivalence and synthesis of causal models. У Bonissone, P.; Henrion, M.; Kanal, L.N.; Lemmer, J.F. (ред.). UAI '90 Proceedings of the Sixth Annual Conference on Uncertainty in Artificial Intelligence. Elsevier. с. 255—270. ISBN 0-444-89264-8. (англ.)
- ↑ Friedman, Nir; Geiger, Dan; Goldszmidt, Moises (November 1997). Bayesian Network Classifiers. Machine Learning. 29 (2-3): 131—163. doi:10.1023/A:1007465528199. Архів оригіналу за 23 лютого 2015. Процитовано 24 лютого 2015. (англ.)
- ↑ Friedman, Nir; Linial, Michal; Nachman, Iftach; Pe'er, Dana (August 2000). Using Bayesian Networks to Analyze Expression Data. Journal of Computational Biology. 7 (3-4): 601—620. doi:10.1089/106652700750050961. PMID 11108481. Процитовано 24 лютого 2015. (англ.)
- ↑ Cussens, James (2011). Bayesian network learning with cutting planes (PDF). Proceedings of the 27th Conference Annual Conference on Uncertainty in Artificial Intelligence: 153—160. Архів оригіналу (PDF) за 27 березня 2022. Процитовано 9 грудня 2016. (англ.)
- ↑ M. Scanagatta, C. P. de Campos, G. Corani, and M. Zaffalon. Learning Bayesian Networks with Thousands of Variables. [Архівовано 2 травня 2018 у Wayback Machine.] In NIPS-15: Advances in Neural Information Processing Systems 28, pages 1855—1863, 2015. (англ.)
- ↑ Petitjean, F.; Webb, G.I.; Nicholson, A.E. (2013). Scaling log-linear analysis to high-dimensional data (PDF). International Conference on Data Mining. Dallas, TX, USA: IEEE. Архів оригіналу (PDF) за 2 червня 2014. Процитовано 9 грудня 2016. (англ.)
- ↑ Nassif, Houssam; Wu, Yirong; Page, David; Burnside, Elizabeth (2012). Logical Differential Prediction Bayes Net, Improving Breast Cancer Diagnosis for Older Women (PDF). American Medical Informatics Association Symposium (AMIA'12). Chicago: 1330—1339. Архів оригіналу (PDF) за 6 травня 2015. Процитовано 18 липня 2014. (англ.)
- ↑ Nassif, Houssam; Kuusisto, Finn; Burnside, Elizabeth S; Page, David; Shavlik, Jude; Santos Costa, Vitor (2013). Score As You Lift (SAYL): A Statistical Relational Learning Approach to Uplift Modeling (PDF). European Conference on Machine Learning (ECML'13). Prague: 595—611. Архів оригіналу (PDF) за 14 квітня 2016. Процитовано 9 грудня 2016. (англ.)
- ↑ M. Scanagatta, G. Corani, C. P. de Campos, and M. Zaffalon. Learning Treewidth-Bounded Bayesian Networks with Thousands of Variables. [Архівовано 26 листопада 2016 у Wayback Machine.] In NIPS-16: Advances in Neural Information Processing Systems 29, 2016. (англ.)
- ↑ а б Russell та Norvig, 2003, с. 496.
- ↑ а б Russell та Norvig, 2003, с. 499.
- ↑ Neapolitan, Richard E. (2004). Learning Bayesian networks. Prentice Hall. ISBN 978-0-13-012534-7. Архів оригіналу за 7 лютого 2017. Процитовано 9 грудня 2016. (англ.)
- ↑ Geiger, Dan; Verma, Thomas; Pearl, Judea (1990). Identifying independence in Bayesian Networks (PDF). Networks. 20: 507—534. doi:10.1177/089443939100900106. (англ.)
- ↑ Richard Scheines, D-separation, архів оригіналу за 22 листопада 2016, процитовано 9 грудня 2016 (англ.)
- ↑ Gregory F. Cooper (1990). The Computational Complexity of Probabilistic Inference Using Bayesian Belief Networks (PDF). Artificial Intelligence. 42: 393—405. doi:10.1016/0004-3702(90)90060-d. Архів оригіналу (PDF) за 29 березня 2017. Процитовано 9 грудня 2016. (англ.)
- ↑ Paul Dagum; Michael Luby (1993). Approximating probabilistic inference in Bayesian belief networks is NP-hard. Artificial Intelligence. 60 (1): 141—153. doi:10.1016/0004-3702(93)90036-b. Архів оригіналу за 24 вересня 2015. Процитовано 9 грудня 2016. (англ.)
- ↑ D. Roth, On the hardness of approximate reasoning [Архівовано 27 січня 2016 у Wayback Machine.], IJCAI (1993) (англ.)
- ↑ D. Roth, On the hardness of approximate reasoning [Архівовано 27 січня 2016 у Wayback Machine.], Artificial Intelligence (1996) (англ.)
- ↑ Paul Dagum; Michael Luby (1997). An optimal approximation algorithm for Bayesian inference. Artificial Intelligence. 93 (1-2): 1—27. doi:10.1016/s0004-3702(97)00013-1. Архів оригіналу за 6 липня 2017. Процитовано 9 грудня 2016. (англ.)
- ↑ Friedman, N.; Linial, M.; Nachman, I.; Pe'er, D. (2000). Using Bayesian Networks to Analyze Expression Data. Journal of Computational Biology. 7 (3–4): 601—620. doi:10.1089/106652700750050961. PMID 11108481. (англ.)
- ↑ Jiang, X.; Neapolitan, R.E.; Barmada, M.M.; Visweswaran, S. (2011). Learning Genetic Epistasis using Bayesian Network Scoring Criteria. BMC Bioinformatics. 12: 89. doi:10.1186/1471-2105-12-89. PMC 3080825. PMID 21453508. Архів оригіналу за 23 вересня 2015. Процитовано 9 грудня 2016.
{{cite journal}}: Обслуговування CS1: Сторінки із непозначеним DOI з безкоштовним доступом (посилання) (англ.) - ↑ J. Uebersax (2004). Genetic Counseling and Cancer Risk Modeling: An Application of Bayes Nets. Marbella, Spain: Ravenpack International. Архів оригіналу за 17 квітня 2016. Процитовано 9 грудня 2016. (англ.)
- ↑ Jiang X, Cooper GF (July–August 2010). A Bayesian spatio-temporal method for disease outbreak detection. J Am Med Inform Assoc. 17 (4): 462—71. doi:10.1136/jamia.2009.000356. PMC 2995651. PMID 20595315. (англ.)
- ↑ Luis M. de Campos; Juan M. Fernández-Luna; Juan F. Huete (2004). Bayesian networks and information retrieval: an introduction to the special issue. Information Processing & Management. Elsevier. 40 (5): 727—733. doi:10.1016/j.ipm.2004.03.001. ISBN 0-471-14182-8. (англ.)
- ↑ Christos L. Koumenides and Nigel R. Shadbolt. 2012. Combining link and content-based information in a Bayesian inference model for entity search. [Архівовано 2 травня 2016 у Wayback Machine.] In Proceedings of the 1st Joint International Workshop on Entity-Oriented and Semantic Search (JIWES '12). ACM, New York, NY, USA, Article 3 , 6 pages. DOI:10.1145/2379307.2379310 (англ.)
- ↑ F.J. Díez; J. Mira; E. Iturralde; S. Zubillaga (1997). DIAVAL, a Bayesian expert system for echocardiography. Artificial Intelligence in Medicine. 10 (1): 59—73. doi:10.1016/s0933-3657(97)00384-9. PMID 9177816. Архів оригіналу за 16 квітня 2016. Процитовано 9 грудня 2016. (англ.)
- ↑ Constantinou, Anthony; Fenton, N.; Neil, M. (2012). pi-football: A Bayesian network model for forecasting Association Football match outcomes. Knowledge-Based Systems. 36: 322—339. doi:10.1016/j.knosys.2012.07.008. (англ.)
- ↑ Constantinou, Anthony; Fenton, N.; Neil, M. (2013). Profiting from an inefficient Association Football gambling market: Prediction, Risk and Uncertainty using Bayesian networks. Knowledge-Based Systems. 50: 60—86. doi:10.1016/j.knosys.2013.05.008. (англ.)
- ↑ G. A. Davis (2003). Bayesian reconstruction of traffic accidents. Law, Probability and Risk. 2 (2): 69—89. doi:10.1093/lpr/2.2.69. (англ.)
- ↑ а б J. B. Kadane & D. A. Schum (1996). A Probabilistic Analysis of the Sacco and Vanzetti Evidence. New York: Wiley. ISBN 0-471-14182-8. (англ.)
- ↑ O. Pourret, P. Naim & B. Marcot (2008). Bayesian Networks: A Practical Guide to Applications. Chichester, UK: Wiley. ISBN 978-0-470-06030-8. Архів оригіналу за 12 жовтня 2008. Процитовано 9 грудня 2016. (англ.)
- ↑ Karvanen, Juha (2014). Study design in causal models. Scandinavian Journal of Statistics. 42: 361—377. doi:10.1111/sjos.12110. (англ.)
- ↑ Trucco, P.; Cagno, E.; Ruggeri, F.; Grande, O. (2008). A Bayesian Belief Network modelling of organisational factors in risk analysis: A case study in maritime transportation. Reliability Engineering & System Safety. 93 (6): 845—856. doi:10.1016/j.ress.2007.03.035. (англ.)
- ↑ Neapolitan, Richard (2009). Probabilistic Methods for Bioinformatics. Burlington, MA: Morgan Kaufmann. с. 406. ISBN 9780123704764. Архів оригіналу за 4 липня 2017. Процитовано 9 грудня 2016. (англ.)
- ↑ Grau J.; Ben-Gal I.; Posch S.; Grosse I. (2006). VOMBAT: Prediction of Transcription Factor Binding Sites using Variable Order Bayesian Trees, (PDF). Nucleic Acids Research, vol. 34, issue W529–W533, 2006. Архів оригіналу (PDF) за 30 вересня 2018. Процитовано 9 грудня 2016. (англ.)
- ↑ Neapolitan, Richard & Xia Jiang (2007). Probabilistic Methods for Financial and Marketing Informatics. Burlingon, MA: Morgan Kaufmann. с. 432. ISBN 0123704774. Архів оригіналу за 20 квітня 2016. Процитовано 9 грудня 2016. (англ.)
- ↑ Shmilovici A., Kahiri Y., Ben-Gal I., Hauser S.(2009. Measuring the Efficiency of the Intraday Forex Market with a Universal Data Compression Algorithm, (PDF). Computational Economics, Vol. 33 (2), 131-154, 2009. Архів оригіналу (PDF) за 22 жовтня 2016. Процитовано 9 грудня 2016. (англ.)
- ↑ Pearl, J. (1985). Bayesian Networks: A Model of Self-Activated Memory for Evidential Reasoning (PDF). Proceedings of the 7th Conference of the Cognitive Science Society, University of California, Irvine, CA. с. 329—334. Архів оригіналу (UCLA Technical Report CSD-850017) за 15 січня 2017. Процитовано 1 травня 2009. (англ.)
- ↑ Bayes, T.; Price, Mr. (1763). Есе щодо розв'язання задачі у Доктрині шансів[en]. Philosophical Transactions of the Royal Society. 53: 370—418. doi:10.1098/rstl.1763.0053. (англ.)
- ↑ Pearl, J. Probabilistic Reasoning in Intelligent Systems. San Francisco CA: Morgan Kaufmann. с. 1988. ISBN 1558604790. Архів оригіналу за 7 лютого 2017. Процитовано 9 грудня 2016. (англ.)
- ↑ Neapolitan, Richard E. (1989). Probabilistic reasoning in expert systems: theory and algorithms. Wiley. ISBN 978-0-471-61840-9. (англ.)
- ↑ Wright, S. (1921). Correlation and Causation (PDF). Journal of Agricultural Research. 20 (7): 557—585. Архів оригіналу (PDF) за 15 січня 2017. Процитовано 9 грудня 2016. (англ.)
- ↑ Judea,, Pearl,. The book of why : the new science of cause and effect (вид. First edition). New York, NY. ISBN 9780465097609. OCLC 1003311466.
Джерела[ред. | ред. код]
- Ben-Gal, Irad (2007). Bayesian Networks. У Ruggeri, Fabrizio; Kennett, Ron S.; Faltin, Frederick W (ред.). Encyclopedia of Statistics in Quality and Reliability (PDF). Encyclopedia of Statistics in Quality and Reliability. John Wiley & Sons. doi:10.1002/9780470061572.eqr089. ISBN 978-0-470-01861-3. Архів оригіналу (PDF) за 23 листопада 2016. Процитовано 9 грудня 2016. (англ.)
- Bertsch McGrayne, Sharon. The Theory That Would not Die. Yale. (англ.)
- Borgelt, Christian; Kruse, Rudolf (March 2002). Graphical Models: Methods for Data Analysis and Mining. Chichester, UK: Wiley. ISBN 0-470-84337-3. Архів оригіналу за 10 червня 2007. Процитовано 13 листопада 2010. (англ.)
- Borsuk, Mark Edward (2008). Ecological informatics: Bayesian networks. У Jørgensen , Sven Erik[en]; Fath, Brian (ред.). Encyclopedia of Ecology. Elsevier. ISBN 978-0-444-52033-3. (англ.)
- Castillo, Enrique; Gutiérrez, José Manuel; Hadi, Ali S. (1997). Learning Bayesian Networks. Expert Systems and Probabilistic Network Models. Monographs in computer science. New York: Springer-Verlag. с. 481–528. ISBN 0-387-94858-9. (англ.)
- Comley, Joshua W.; Dowe, David L. (June 2003). General Bayesian networks and asymmetric languages. Proceedings of the 2nd Hawaii International Conference on Statistics and Related Fields. Hawaii. Архів оригіналу за 4 серпня 2016. Процитовано 13 листопада 2010. (англ.)
- Comley, Joshua W.; Dowe, David L. (2005). Minimum Message Length and Generalized Bayesian Nets with Asymmetric Languages. У Grünwald, Peter D.; Myung, In Jae; Pitt, Mark A. (ред.). Advances in Minimum Description Length: Theory and Applications. Neural information processing series. Cambridge, Massachusetts: Bradford Books (MIT Press) (опубліковано опубліковано April 2005). с. 265—294. ISBN 0-262-07262-9. Архів оригіналу за 4 серпня 2016. Процитовано 13 листопада 2010. (Ця праця ставить дерева рішень у внутрішніх вузлах баєсових мереж із застосуванням мінімальної довжини повідомлень [Архівовано 9 лютого 2006 у Wayback Machine.] (англ. MML). Готову до друку кінцеву версію було представлено 15 жовтня 2003 року. Раніша версія: Comley and Dowe (2003) [Архівовано 4 серпня 2016 у Wayback Machine.], .pdf [Архівовано 10 лютого 2006 у Wayback Machine.].) (англ.)
- Darwiche, Adnan (2009). Modeling and Reasoning with Bayesian Networks. Cambridge University Press. ISBN 978-0521884389. (англ.)
- Dowe, David L. (2010). MML, hybrid Bayesian network graphical models, statistical consistency, invariance and uniqueness [Архівовано 14 квітня 2016 у Wayback Machine.], in Handbook of Philosophy of Science (Volume 7: Handbook of Philosophy of Statistics), Elsevier, [2] [Архівовано 25 квітня 2012 у Wayback Machine.] ISBN 978-0-444-51862-0, pp 901–982 [Архівовано 14 квітня 2016 у Wayback Machine.]. (англ.)
- Fenton, Norman; Neil, Martin E. (November 2007). Managing Risk in the Modern World: Applications of Bayesian Networks — A Knowledge Transfer Report from the London Mathematical Society and the Knowledge Transfer Network for Industrial Mathematics. London (England): London Mathematical Society. (англ.)
- Fenton, Norman; Neil, Martin E. (23 липня 2004). Combining evidence in risk analysis using Bayesian Networks (PDF). Safety Critical Systems Club Newsletter. Т. 13, № 4. Newcastle upon Tyne, England. с. 8—13. Архів оригіналу (PDF) за 27 вересня 2007.
{{cite news}}: Cite має пустий невідомий параметр:|df=(довідка) (англ.) - Andrew Gelman; John B Carlin; Hal S Stern; Donald B Rubin (2003). Part II: Fundamentals of Bayesian Data Analysis: Ch.5 Hierarchical models. Bayesian Data Analysis. CRC Press. с. 120–. ISBN 978-1-58488-388-3. Архів оригіналу за 7 лютого 2017. Процитовано 9 грудня 2016. (англ.)
- Heckerman, David (1 березня 1995). Tutorial on Learning with Bayesian Networks. У Jordan, Michael Irwin (ред.). Learning in Graphical Models. Adaptive Computation and Machine Learning. Cambridge, Massachusetts: MIT Press (опубліковано опубліковано 1998). с. 301—354. ISBN 0-262-60032-3. Архів оригіналу за 19 липня 2006. Процитовано 13 листопада 2010..
- Також з'являється як Heckerman, David (March 1997). Bayesian Networks for Data Mining. Data Mining and Knowledge Discovery[en]. 1 (1): 79—119. doi:10.1023/A:1009730122752.
- Раніша версія з'являється як, Microsoft Research, March 1, 1995. Ця праця як про параметричне, так і про структурне навчання в баєсових мережах. (англ.)
- Jensen, Finn V; Nielsen, Thomas D. (6 червня 2007). Bayesian Networks and Decision Graphs. Information Science and Statistics series (вид. 2nd). New York: Springer-Verlag. ISBN 978-0-387-68281-5. (англ.)
- Karimi, Kamran; Hamilton, Howard J. (2000). Finding temporal relations: Causal bayesian networks vs. C4. 5 (PDF). Twelfth International Symposium on Methodologies for Intelligent Systems. Архів оригіналу (PDF) за 7 травня 2016. Процитовано 9 грудня 2016. (англ.)
- Korb, Kevin B.; Nicholson, Ann E. (December 2010). Bayesian Artificial Intelligence. CRC Computer Science & Data Analysis (вид. 2nd). Chapman & Hall (CRC Press). doi:10.1007/s10044-004-0214-5. ISBN 1-58488-387-1. (англ.)
- Lunn, David; Spiegelhalter, David; Thomas, Andrew; Best, Nicky та ін. (November 2009). The BUGS project: Evolution, critique and future directions. Statistics in Medicine. 28 (25): 3049—3067. doi:10.1002/sim.3680. PMID 19630097. (англ.)
- Neil, Martin; Fenton, Norman E.; Tailor, Manesh (August 2005). Greenberg, Michael R. (ред.). Using Bayesian Networks to Model Expected and Unexpected Operational Losses (PDF). Risk Analysis[en]. 25 (4): 963—972. doi:10.1111/j.1539-6924.2005.00641.x. PMID 16268944. Архів оригіналу (pdf) за 27 вересня 2007. Процитовано 13 листопада 2010. (англ.)
- Pearl, Judea (September 1986). Fusion, propagation, and structuring in belief networks. Artificial Intelligence[en]. 29 (3): 241—288. doi:10.1016/0004-3702(86)90072-X. (англ.)
- Pearl, Judea (1988). Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Representation and Reasoning Series (вид. 2nd printing). San Francisco, California: Morgan Kaufmann[en]. ISBN 0-934613-73-7. (англ.)
- Pearl, Judea; Russell, Stuart (November 2002). Bayesian Networks. У Arbib, Michael A. (ред.). Handbook of Brain Theory and Neural Networks. Cambridge, Massachusetts: Bradford Books (MIT Press). с. 157—160. ISBN 0-262-01197-2. (англ.)
- Russell, Stuart J.; Norvig, Peter (2003), Artificial Intelligence: A Modern Approach (англ.) (вид. 2nd), Upper Saddle River, New Jersey: Prentice Hall, ISBN 0-13-790395-2
- Zhang, Nevin Lianwen; Poole, David (May 1994). A simple approach to Bayesian network computations. Proceedings of the Tenth Biennial Canadian Artificial Intelligence Conference (AI-94). Banff, Alberta: 171—178. This paper presents variable elimination for belief networks. (англ.)
Література[ред. | ред. код]
- Computational Intelligence: A Methodological Introduction by Kruse, Borgelt, Klawonn, Moewes, Steinbrecher, Held, 2013, Springer, ISBN 9781447150121 (англ.)
- Graphical Models — Representations for Learning, Reasoning and Data Mining, 2nd Edition, by Borgelt, Steinbrecher, Kruse, 2009, J. Wiley & Sons, ISBN 9780470749562 (англ.)
- Bayesian Netwrks and BayesiaLab — A practical introduction for researchers by Stefan Conrady and Lionel Jouffe (англ.)
- Бідюк, П.І.; Кузнєцова, Н.В. (2007). Основні етапи побудови і приклади застосування мереж Байєса (PDF). Системні дослідження та інформаційні технології. Київ: ІПСА. 4. ISSN 1681–6048. Архів оригіналу (PDF) за 2 квітня 2015. Процитовано 30 березня 2015.
{{cite journal}}: Перевірте значення|issn=(довідка)
Посилання[ред. | ред. код]
- A tutorial on learning with Bayesian Networks (англ.)
- An Introduction to Bayesian Networks and their Contemporary Applications [Архівовано 21 травня 2017 у Wayback Machine.] (англ.)
- Інтернет-посібник з баєсових мереж та імовірності [Архівовано 4 травня 2009 у Wayback Machine.] (англ.)
- Вебзастосунок для створення баєсових мереж та виконання їх методом Монте-Карло (англ.)
- Continuous Time Bayesian Networks [Архівовано 9 жовтня 2018 у Wayback Machine.] (англ.)
- Баєсові мережі: пояснення та аналогія (англ.)
- Живий урок з навчання баєсовим мережам [Архівовано 15 квітня 2021 у Wayback Machine.] (англ.)
- A hierarchical Bayes Model for handling sample heterogeneity in classification problems [Архівовано 9 січня 2015 у Wayback Machine.], пропонує модель класифікації, яка враховує невизначеність, пов'язану з вимірюванням повторюваних зразків. (англ.)
- Hierarchical Naive Bayes Model for handling sample uncertainty [Архівовано 28 вересня 2007 у Wayback Machine.], показує, як виконувати класифікацію та навчання з неперервними та дискретними змінними з повторюваними вимірюваннями. (англ.)
- Сергей Николенко. Лекции № 8 [Архівовано 29 грудня 2009 у Wayback Machine.], № 9 [Архівовано 1 січня 2015 у Wayback Machine.] и № 10 [Архівовано 1 січня 2015 у Wayback Machine.], посвященные байесовским сетям доверия. Курс «Самообучающиеся системы» (рос.)




























































