Квадрика
| Ця стаття містить правописні, лексичні, граматичні, стилістичні або інші мовні помилки, які треба виправити. |
Квадрика — n-мірна гіперповерхня в n+1-мірному просторі, задана як множина нулів многочлена другого степеня. Якщо ввести координати {x1, x2, ..., xn+1} (в евклідовому або афінному просторі), загальне рівняння квадрики має вигляд[1]
Це рівняння можна переписати більш компактно в матричних позначеннях:
де x = {x1, x2, ..., xn+1} — вектор-рядок, xT — транспонований вектор, Q — матриця розміру (n+1)×(n+1) (передбачається, що хоча б один її елемент ненульовий), P — вектор-рядок, а R — константа. Найбільш часто розглядають квадрики над дійсними або комплексними числами. Визначення можна поширити на квадрики в проєктивному просторі.
Більш загально, множину нулів системи поліноміальних рівнянь можна розглядати як алгебраїчний многовид. Таким чином, квадрика є (аффінним або проєктивним) алгебраїчним многовидом другого ступеня і ковимірності 1.
Квадрика в евклідовому просторі[ред. | ред. код]
Квадрика на евклідовій площині відповідає випадку n = 1, тобто є кривими. Зазвичай їх називають не квадриками, а коніками або конічними перетинами.

Квадрики в (тривимірному дійсному) евклідовому просторі мають розмірність n = 2 і називаються поверхнями другого порядку. Провівши ортогональну заміну базису, будь-яку квадрику в евклідовому просторі можна звести до нормальної форми. У тривимірному евклідовому просторі існує 17 таких форм.[2] З них 5 є невиродженими (тобто відповідна їм білінійна форма Q є невиродженою). Вироджені форми включають в себе площині, прямі, точки і навіть квадрику без дійсних точок.[3]
| Невироджені дійсні квадрики в евклідовому просторі | ||
|---|---|---|
| Еліпсоїд | 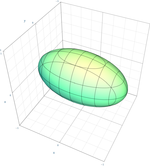
| |
| Сфероїд (спеціальна форма еліпсоїда) |  
| |
| Сфера (спеціальна форма сфероїда) | 
| |
| Еліптичний параболоїд | 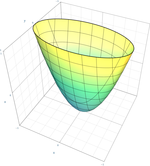
| |
| Круговий параболоїд (спеціальна форма еліптичного параболоїда) | 
| |
| Гіперболічний параболоїд | 
| |
| Однопорожнинний гіперболоїд | 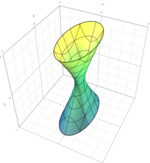
| |
| Двопорожнинний гіперболоїд | 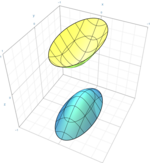
| |
| Вироджені квадрики в евклідовому просторі | ||
| Еліптичний конус | 
| |
| Круговий конус (спеціальна форма еліптичного конуса) | 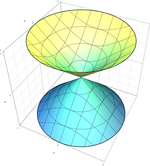
| |
| Еліптичний циліндр | 
| |
| Круговий циліндр (спеціальна форма еліптичного циліндра) | 
| |
| Гіперболічний циліндр | 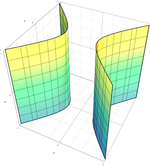
| |
| Параболічний циліндр | 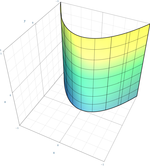
| |
Афінний та проєктивний простір[ред. | ред. код]
Класифікація квадрик у тривимірному афінному просторі збігається з класифікацією квадрик в евклідовому просторі.[4] Різниця полягає в тому, що будь-які дві квадрики з одного класу можна перевести одну в одну афінним перетворенням, тоді як відповідне ортогональне перетворення існує не завжди (наприклад, еліпсоїд неможливо перевести рухом в еліпсоїд ).
Від квадрики в афінному просторі можна перейти до квадрики в проєктивному просторі, ввівши однорідні координати. Нехай у афінному просторі введені координати тоді в рівнянні квадрики достатньо помножити лінійні члени на а вільний член на Рівняння проєктивної квадрики в однорідних координатах має вигляд
Без обмеження спільності можна вважати, що матриця симетрична, тобто Проєктивна квадрика називається невиродженою, якщо відповідна їй квадратична форма невирождена.
У дійсному проєктивному просторі, відповідно до закону інерції, будь-яку невироджену квадратну форму можна звести (проєктивним перетворенням) до вигляду
Оскільки сигнатура квадратичної форми є її інваріантом, в розмірності n = 2 існує рівно три класи еквівалентності:
Еліпсоїд, еліптичний параболоїд і двопорожнинний гіперболоїд належать другому класу, а гіперболічний параболоїд і однопорожнинний гіперболоїд — третьому (останні дві квадрики є прикладами лінійчатих поверхонь). Жодна квадрика в дійсному проєктивному просторі не належить першому класу, тому що відповідне рівняння визначає точку, а не поверхню. У комплексному проєктивному просторі всі невироджені квадрики еквівалентні.
Імовірність і статистика[ред. | ред. код]
Еліптичний розподіл, узагальнює багатовимірний нормальний розподіл і використовується в галузі фінансів, може бути визначеним з точки зору його функцій щільності. Коли він існує, функції щільності F мають структуру:
де це масштабний коефіцієнт, це -мірний випадковий вектор-рядок з середнім вектором , це позитивна матриця, яка пропорційна коваріаційній матриці, якщо остання існує, та є функцією, що відображає від невід'ємних до невід'ємних чисел кінцеву площу під кривою.[5] Багатовимірний нормальний розподіл є окремим випадком, в якому для квадратичної форми .
Таким чином, функція щільності є скалярним перетворенням квадратичного виразу. Крім того, рівняння для будь-якої поверхні з щільністю заявляє, що квадратичний вираз дорівнює деякій константі, що відносяться до цього значення щільності.
Примітки[ред. | ред. код]
- ↑ Silvio Levy. Quadrics. Geometry Formulas and Facts, excerpted from 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press) (англ.). Архів оригіналу за 18 Липня 2018. Процитовано 30 липня 2013.
- ↑ Sameen Ahmed Khan. Quadratic Surfaces in Science and Engineering (PDF) (англ.). Bulletin of the IAPT, 2(11), 327—330 (November 2010). (Publication of the Indian Association of Physics Teachers). Архів (PDF) оригіналу за 13 серпня 2013. Процитовано 30 липня 2013.
- ↑ Stewart Venit, Wayne Bishop, Elementary Linear Algebra (fourth edition), International Thompson Publishing, 1996.
- ↑ П. С. Александров. Курс аналитической геометрии и линейной алгебры. С.275.
- ↑ Frahm, G., Junker, M., & Szimayer, A. (2003). Elliptical copulas: applicability and limitations. Statistics & Probability Letters, 63(3), 275—286.


































