Когерентні стани
Когерентними станами в квантовій механіці називають певні стани квантового гармонічного осцилятора, динаміка яких найближча до коливань класичного осцилятора. Першим із ними зустрівся Ервін Шредінгер у 1926 році, шукаючи розв'язки рівняння Шредінгера, що задовольняли б принципу відповідності[1]. Модель квантового осцилятора, а отже когерентні стани, фігурують в описі широкого класу фізичних систем[2]. Наприклад, когерентний стан описує коливання частинки в квадратичному потенціалі.
Ці стани, які першим запровадив Джон Клаудер[3], є власними векторами оператора пониження й утворюють надповний базис. У квантову теорію світла (квантову електродинаміку) та теорію інших бозонних квантових полів когерентні стани увійшли завдяки роботі 1963 року Роя Глаубера. Когерентний стан описує стан системи, в якій хвильовий пакет основного стану зміщено з початку системи координат. Його можна асоціювати з класичним розв'язком коливань частинки з амплітудою, еквівалентною зміщенню.
Концепцію когерентних станів було узагальнено, що перевело її на новий рівень абстракції. Вона стала важливою темою досліджень математичної фізики та прикладної математики. Її застосовують для розв'язання широкого кола задач: від квантування до обробки сигналів та зображень. Тому когерентні стани власне гармонічного осцилятора іноді називають канонічними, стандартними, гаусовими або осциляторними.
У квантовій оптиці[ред. | ред. код]

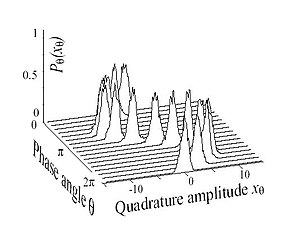

У квантовій оптиці когерентним станом називають стан квантованого електромагнітного поля[2][5][6], який найкраще описує когерентність та має поведінку схожу на класичну. Ервін Шредінгер 1926 року[1], намагаючись відшукати розв'язок рівняння Шредінгера, що задовольняв би принцип відповідності, вивів його як стан із найменшою невизначеністю гаусового хвильового пакету. Це стан найменшої невизначеності, єдиний параметр якого вибирається так, що зробити дисперсію (в натуральних безрозмірних одиницях стандартне відхилення) положення та імпульсу однаковими. При високій енергії обидві дисперсії однаково малі.
Далі, на відміну від власних станів енергії системи, еволюція когерентного стану зосереджена вздовж класичної траєкторії. Лінійний квантовий осцилятор, а отже, когерентні стани з'являються у широкому колі фізичних систем: в квантовій теорії світла та теорії інших бозонних квантових полів.
Тоді як гаусів хвильовий пакет із мінімальною невизначеністю був доволі відомим, на нього не звертали особливої уваги до того, як Рой Глаубер 1963 року не дав повного квантовотеоретичного опису когерентності електромагнітного поля[7]. У цьому відношенні не слід забувати паралельного внеску Сударшана[8] (у статті Глаубера є примітка, де написано: "Використання цих станів як генераторів для станів квантів належить Джуліану Швінгеру[9]). Глауберу потрібно було описати ефект Генбері-Брауна та Твісса, який дозволяє утворення інтерференційних картин із дуже широкою базою (сотні та тисячі кілометрів), які можна використати для визначення діаметрів зір. Одночасно відкрився шлях до глибшого розуміння когерентності.
Класична оптика описує світло як електромагнітні хвилі, що випромінюються джерелом. Когерентні лазери часто описують як світло, випромінене з багатьох джерел, що коливаються в фазі. Власне, в квантовій теорії говорити, що фотон перебуває в фазі з іншим, не зовсім правильно. Випромінювання лазера відбувається в резонаторі, власна частота якого дорівнює частоті електронного переходу в атомі, який постачає полю енергію. Енергія резонансної моди наростає, імовірність вимушеного випромінювання в цій моді зростає. Це створює додатний обернений зв'язок, завдяки якому амплітуда резонантної моди експоненціально росте до межі, визначеної якимось нелінійним ефектом. З іншого боку, випромінювання світла лампочкою відбувається в неперервний спектр мод, і немає жодного фактора, що міг би виділити одну моду серед інших. Тому випромінювання дуже випадкове в просторі й часі. А от у лазері, випромінювання відбувається в резонантну моду, яка має високий ступінь когерентності.
Власні енергетичні стани гармонічного осцилятора (наприклад, маси за пружинці, коливань кристалічної ґратки в твердому тілі, коливань електромагнітного поля) є станами з фіксованими числами. Стан Фока (наприклад, одиничний фотон) є найбільш корпускулярним: число частинок відоме точно, а фаза зовсім не визначена. У когерентному стані квантова невизначеність розподілена порівну між канонічно спряженими координатами: положенням та імпульсом, і відносні невизначеності фази та амплітуди приблизно однакові й малі при великих значеннях амплітуди.
Квантовомеханічне означення[ред. | ред. код]
Математично когерентний стан визначається як єдиний власний стан оператора знищення â, асоційований з власним значенням α. Формально:
Оскільки â не є ермітовим оператором, α — загалом комплексне число. Записуючи |α| та θ називають амплітудою та фазою стану .
Фізично ця формула означає, що когерентний стан не змінюється, якщо вилучити одне збудження поля, або, іншими словами, частинки. Власне значення оператора знищення, виражене через власні значення оператора енергії, має пуассонів розподіл. Розподіл Пуассона є необхідною та достатньою умовою того, щоб всі вимірювання були статистично незалежними. Для порівняння — в одночастинкових станах (стан Фока ): якщо частинку детектовано, то імовірність детектувати іншу дорівнює нулю.
Доведення використовує безрозмірні оператори, X та P, які зазвичай називають у квантовій оптиці польовими квадратурами. Ці оператори зв'язані з операторами положення та імпульсу матеріальної точки з масою m на пружинці жорсткості k,
- де

Для оптичного поля
- та
є дійсною та уявною частинами моди електричного поля.
Через ці безрозмірні оператори гамільтоніан системи записується
- де
Коли Ервін Шредінгер запровадив гаусові хвильові пакети з мінімальною невизначеністю, він шукав стани, що були б найбільше схожі на класичні. Квантовий стан гармонічного осцилятора, що мінімізує співвідношення невизначеності, в якому невизначеність була б рівно розподіленою між X та P, задовольняє рівняння
або еквівалентно
а тому
Отже, якщо (∆X−∆P)² ≥ 0, Шредінгер виявив, що стан гармонічного осцилятора із найменшою невизначеністю є власним станом (X+iP). Оскільки â є (X+iP), саме цей стан і є когерентним станом.
Використовуючи позначення багатофотонних станів, Глаубер визначив, що всі стани з повною когерентністю будь-якого порядку є власними станами оператора знищення — формально в математичному сенсі це саме той стан, який знайшов Шредінгер. Назва когерентний стан увійшла в ужиток після роботи Глаубера.
Якщо невизначеність мінімальна, але не обов'язково рівно розподілена між X та P, стан називають стисненим когерентним станом.
Положення когерентного стану на комплесній площині (фазовому прострі) центроване на значенні положення та імпульсу класичного осцилятора з фазою θ та амплітудою |α|, що визначаються власним значенням α (або тим самим значенням електричного поля, що й для електромагнітної хвилі). Як показано на рис. 5, невизначеність, рівно розподілена в усіх напрямках, представлена диском із діаметром 1⁄2. При зміні фази когерентний стан обертається навколо початку системи координат, а диск не спотворюється і не розпливається. Це виглядає майже так, наче квантовий стан — точка в фазовому просторі.

Оскільки невизначеність (а отже шум при вимірюваннях) залишається сталою зі значенням 1⁄2 при зростанні амплітуди коливань, стан дедалі більше нагадує синусоїдальну хвилю, показану на рис. 1. А, оскільки вакуумний стан є когерентним станом з α=0, усі когерентні стани мають однакову з вакуумом невизначеність. Тому квантовий шум можна трактувати як зумовлений флуктуаціями вакууму.
Позначення не є станом Фока. Наприклад, коли α=1, це не слід плутати з для однофотонного стану Фока, який теж позначають . Вираз з α=1 є насправді пуассоновим розподілом багатьох станів з одиничним середнім значенням кількості фотонів.
Формальний розв'язок рівняння на власні значення є вакуумним станом, зміщеним на α у фазовому просторі, тобто, його можна отримати дією унітарного оператора зміщення D(α) на вакуум
- ,
де â = X+iP, а ↠= X-iP.
У цьому легко переконатися, як практично в усіх результатах з когерентними станами, використовуючи представлення когерентних станів у базисі станів Фока
де |n〉 — власні вектори енергії (числа частинок) гамільтоніана
Для відповідного розподілу Пуассона імовірність детектування n фотонів дорівнює
Аналогічно, середнє число фотонів у когерентному стані дорівнює
а дисперсія:
- .
Тобто, стандартне відхилення числа детектованих частинок збільшується пропорційно квадратному кореню їхнього числа. Тому в граничному випадку великих α, детектування еквівалентні тому, що спостерігається для стабільної класичної хвилі.
Ці результати застосовні до детектувань одного детектора, а тому стосуються когерентності першого порядку. Однак, кореляції відліків кількох детекторів вимагають когерентності вищих порядків (наприклад, два детектори вимагають кореляції інтенсивності та когерентності другого порядку). Квантова когерентність, визначена за Глаубером, має справу з кореляціями n-го порядку (n-тий ступінь когерентності) для всіх n. Кореляції усіх порядків досконало когерентного стану дорівнюють 1.
Робота Глаубера побачила світ в зв'язку з результатами Генбері-Брауна та Твісса, що продемонстрували далеку (сотні й тисячі кілометрів) інтерференцію першого порядку, використовуючи флуктуації інтенсивності (відсутність когеренції другого порядку) та фільтр з вузькою смугою пропускання (часткова когерентність першого порядку в кожному з детекторів. (Можна уявити дуже короткоплинну, майже миттєву інтерференційну картину на двох детекторах, що виникає завдяки вузьким фільтрам і випадково стрибає через зсув відносної різниці фаз. При використанні лічильника збігів нестійка інтеренференційна картина проявляється сильніше під час зростання інтенсивності [спільне для обох фаз], і ця картина перекриватиме фоновий шум.) Майже вся оптика мала справу з когерентністю першого порядку. Результати Генбері-Брауна та Твісса змусили Глаубера розглянути когерентність вищих порядків, і він знайшов квантовомеханічний опис когерентності електромагнітного поля будь-якого порядку (і квантово теоретичний опис відношення сигналу плюс шуму). Він запропонував назву когерентний стан і показав, що ці стани виникають, коли класичний електричний струм взаємодіє з електромагнітним полем.
При α ≫ 1, виходячи з рис. 5, прості геметричні міркування дають Δθ |α | = 1/2. Виглядає, що виграш у невизначеності числа частинок спряжений з програшем у невизначеності фази, Δθ Δn = 1/2, що іноді інтерпретують як співвідношення невизначеності число-фаза; але таке співвідношення не є математично строгим: у квантовій механіці немає однозначно визначеного оператора фази[10] [11] [12] [13] [14] [15] [16] [17].
Хвильова функція когерентного стану[ред. | ред. код]

Щоб знайти хвильову функцію когерентного стану, тобто хвильовий пакет, що відповідає найменшій невизначеності, найлегше розпочати з квантового осцилятора в картині Гейзенберга для когерентного стану .
Когерентний стан є власним станом оператора знищення в картині Гейзернберга
Неважко переконатися, що те ж власне значення виникає і в картині Шредінгера
- .
У координатному поданні записується диференціальне рівняння
розв'язок якого
де θ(t) — ще не визначена фаза, яку можна знайти вимагаючи, щоб хвильова функція задовольняла рівняння Шредінгера.
- де
тож σ — початкова фаза.
Середнє положення та імпульс цього мінімального хвильового пакету Шредінгера ψ(α) осцилюють наче в класичній системі,
Густина ймовірності залишається гаусовою з центром на цьому залежному від часу середньому
Математичні властивості канонічних когерентних станів[ред. | ред. код]
Описані когерентні стани мають три взаємно еквівалентні риси, оскільки кожна з них повністю визначає стан . Ці риси:
- Когерентні стани є власними функціями оператора знищення: .
- Їх можна отримати з вакууму за допомогою унітарного оператора зміщення: .
- Вони є станами з мінімальною (збалансованою) невизначеністю: .
Кожну з цих рис можна узагальнити, і ці узагальнення, загалом різні, вивчаються математичною фізикою. Важливо відзначити, що когерентні стани мають риси дуже відмінні від станів Фока, наприклад два різні когерентні стани не ортогональні:
оскільки вони є власними векторами несамоспряженого опертора знищення â.
Тому, якщо осцилятор перебуває в квантовому стані , він також може з ненульовою імовірністю бути в іншому квантовому стані (але чим далі стани перебувають у фазовому просторі, тим менша ця імовірність). Однак будь-який стан можна розкласти на когерентні. Тому вони утворюють надповний базис, в якому можна діагонально розкласти будь-який стан. Це є характерною рисою зображення Сударшана-Глаубера.
Відношення замикання можна записати, резолювавши одиничний оператор I на векторному просторі квантових станів:
Іншою особливістю є те, що не має парного собі власного кет-вектора (а â не має парного власного бра-вектора). Наступне співвідношення задає найближчу формальну заміну і може пригодитися в технічних розрахунках
Останній стан відомий під назвами «стан Агарвала» або когерентний стан із доданим фотоном. Його позначають
Нормалізовані стани Агарвала порядку n можна записати як
Згадану резолюцію одиничного оператора можна вивести (обмежуючись для простоти однією просторовою розмірністю), взявши матричні елементи між станами положення: з обох сторін рівняння. Справа це одразу дає δ(x-y). Зліва теж саме виходить після вставки
з попереднього розділу (час довільний), а тоді проінтегрувавши по й використовуючи using the Фур'є образ дельта-функції, і далі беручи гаусів інтеграл по .
Гаусів хвильовий пакет Шредінгера можна отримати зі значення
Резолюцію одиничного оператора можна також виразити через положення та імпульс частинки. Для кожної з просторових координат (використовуючи адаптовану нотацію з новим значенням для ),
замикання когерентних станів набирає форми
Це можна вставити в будь-яке очікуване значення в квантовій механіці, співвідносячи його з деяким квазікласичним інтегралом у фазовому просторі та пояснюючи, зокрема, походження множника нормування в класичній функції розподілу, сумісній з квантовою механікою.
Окрім того, що когерентний стан є точним власним станом оператора знищення, він також є наближеним спільним власним станом положення та імпульсу. Знову обмежуючись одновимірним випадком,
Похибка в цих наближеннях вимірюється в невизначеностях положення та імпульсу:
Теплові когерентні стани[ред. | ред. код]
Одномодовий тепловий когерентний стан[18] можна отримати, зміщуючи змішаний стан у фазовому просторі, аналогічно до зміщення вакуумного стану з метою утворити когерентний стан. Матриця густини когерентного теплового стану записується через оператори у вигляді
де — оператор зміщення, що генерує когерентний стан з комплексною амплітудою , а . Статистична сума дорівнює
Використовуючи розклад одиничного оператора по станах Фока , оператор густини можна задати в наступній формі
де — зміщені фокові стани. Коли температура прямує до нуля
що є матрицею густини для когерентного стану. Середнє число фотонів у цьому стані можна розрахувати так
де для останнього члена можна записати
Як наслідок
де є середнім числом фотонів, обчисленим стосовно теплового стану. Тут, для спрощення позначень
і можна прямо записати
У граничному випадку , що сумісно з виразом для матриці густини при нулі температури. Аналогічно, дисперсію числа фотонів можна оцінити як
з . Звідси висновок — другий момент розподілу не можна розділити на тепловий та квантовий, на відміну від середнього значення (першого моменту). У цьому сенсі фононна статистика зміщеного теплового стану не описується сумою розподілів Пуассона та Больцмана. Розподіл початкового теплового стану в фазовому просторі уширюється внаслідок когерентного зміщення.
Когерентні стани в конденсаті Бозе-Ейнштейна[ред. | ред. код]
Бозе-конденсат виникає тоді, коли багато атомів-бозонів збираються в одному квантовому стані, стані з найнижчою енергією. Основний стан термодинамічної системи стає макроскопічно заселеним нижче певної критичної температури, приблизно коли температурна довжина хвилі де Бройля починає перевищувати міжатомну відстань. Вважається, що з Бозе-Ейнштейнівською конденсацією зв'язана надплинність в гелії-4. Але 4He має сильну міжатомну взаємодію, і рідинний структурний фактор (статистика другого порядку) грає важливу роль. Використання когерентного стану при описі надплинної компоненти 4He дає непогану оцінку для конденсованої та неконденсованої фракцій в надплинності, сумісну з результатами дослідів з розсіяння повільних нейтронів[19][20][21]. Більшість особливих надплинних властивостей прямо слідують з моделювання надплинної компоненти як когерентного стану; він діє наче макроскопічно заселений одночастинковий стан із добре визначеною амплітудою та фазою, що зберігаються в усьому об'ємі. (Частка надплинної компоненти зростає від нуля при температурі переходу до 100% при абсолютному нулі. Але фракція конденсату досягає при Т=0 К тільки приблизно 6%[22].).
Ще на початку дослідження надплинності Олівер Пенроуз та Ларс Онсагер запропонували характеризувати надплинність певним параметром порядку[23]. Його функцію виконувала факторизована макроскопічна компонента (макроскопічне власне значення) у зведеній матриці густини першого порядку. Пізніше Янг[24] запропонував загальніший параметр порядку для макроскопічної квантової конерентності, який отримав назву «недіагональний далекий порядок» (ODLRO)[25], що дозволило включити не тільки бозони, а й ферміони. ODLRO існує як лише є макроскопічно велика факторизована компонента (власне значення) у зведеній матриці густини будь-якого порядку. Надплинність відповідає великій факторизованій компоненті в зведеній матриці густини першого порядку. (А зведені матриці густини усіх вищих порядків мають аналогічну поведінку). Надпровідність вимагає великої факторизованої компоненти у зведеній матриці густини другого порядку (куперівські пари).
Зведені матриці густини, що описують квантову когерентність у надпровідних рідинах, формально аналогічні кореляційним функціям, що задають порядки когерентності у електромагнітному випромінюванні. Як одні, так і інші є прикладами макроскопічної квантової когеренції. Макроскопічно велика когерентна компонента в електромагнітному полі плюс шум формально аналогічні великій надплинній компоненті плюс нормальна компонента в дворідинній моделі надплинності.
Когерентність в надплинності не є властивістю будь-якої підмножини атомів гелію — це різновид колективного явища, в якому беруть участь усі атоми. Те ж саме можна сказати про утворення куперівських пар при надпровідності.
Узагальнення[ред. | ред. код]
Гілмор і Переломов незалежно один від одного показали, що побудову когерентного стану можна розглядати як задачу теорії груп, і що ці когерентні стани можна асоціювати з групами, відмінними від групи Гайзенберга, яка приводить до канонічних когерентних станів[26][27][28][29]. Що більше, ці когерентні стани можна узагальнити до квантових груп.
У квантовій теорії поля та теорії струн когерентні стани узагальнюються на випадок нескінченного числа ступенів вільності й використовуються для визначення вакуумного стану з вакуумним середнім іншим, ніж для початкового вакууму.
У одновимірних багаточастинкових квантових системах з ферміонними ступенями вільності низькоенергетичні збуджені стани можна апроксимувати когерентними станами з оператором бозонного поля, що описує збудження типу частинка-дірка. Це називають бозонізацією.
Гаусові когерентні стани нерелятивістської механіки можна узагальнити на релятивістські когерентні стани частинок, що описуються рівняннями Клейн-Гордона та Дірака[30][31][32].
Когерентні стани фігурують також у роботах із петльової квантової гравітації та для побудови напівкласичної канонічної квантової загальної теорії відносності[33][34]
Виноски[ред. | ред. код]
- ↑ а б E. Schrödinger, Der stetige Übergang von der Mikro- zur Makromechanik, Naturwissenschaften 14 (1926) 664-666.
- ↑ а б J.R. Klauder and B. Skagerstam, Coherent States, World Scientific, Singapore, 1985.
- ↑ J. R. Klauder, The action option and a Feynman quantization of spinor fields in terms of ordinary c-numbers, Ann. Physics 11 (1960) 123–168.
- ↑ G. Breitenbach, S. Schiller, and J. Mlynek, Measurement of the quantum states of squeezed light [Архівовано 4 Березня 2016 у Wayback Machine.], Nature 387 (1997) 471-475
- ↑ W-M. Zhang, D. H. Feng, and R. Gilmore, Coherent states: Theory and some applications, Rev. Mod. Phys. 62 (1990) 867-927.
- ↑ J-P. Gazeau, Coherent States in Quantum Physics, Wiley-VCH, Berlin, 2009.
- ↑ R.J. Glauber, Coherent and incoherent states of radiation field,Phys. Rev. 131 (1963) 2766-2788.
- ↑ E.C.G. Sudarshan, Equivalence of semiclassical and quantum mechanical descriptions of statistical light beams, Phys. Rev. Lett. 10 (1963) 277-279.
- ↑ J. Schwinger, Theory of quantized fields. III, Phys. Rev. 91 (1953) 728-740
- ↑ L. Susskind and J. Glogower, Quantum mechanical phase and time operator,Physics 1 (1963) 49.
- ↑ P. Carruthers and M.N. Nieto, Phase and angle variables in quantum mechanics,Rev. Mod. Phys. 40 (1968) 411-440.
- ↑ S.M. Barnett and D.T. Pegg, On the Hermitian optical phase operator,J. Mod. Opt. 36 (1989) 7-19.
- ↑ P. Busch, M. Grabowski and P.J. Lahti, Who is afraid of POV measures? Unified approach to quantum phase observables, Ann. Phys. (N.Y.) 237 (1995) 1-11.
- ↑ V.V. Dodonov, 'Nonclassical' states in quantum optics: a 'squeezed' review of the first 75 years, J. Opt. B: Quantum Semiclass. Opt. 4 (2002) R1-R33.
- ↑ V.V. Dodonov and V.I.Man'ko (eds), Theory of Nonclassical States of Light, Taylor \& Francis, London, New York, 2003.
- ↑ A. Vourdas, Analytic representations in quantum mechanics, J. Phys. A: Math. Gen. 39 (2006) R65-R141.
- ↑ J-P. Gazeau,Coherent States in Quantum Physics, Wiley-VCH, Berlin, 2009.
- ↑ J. Oz-Vogt, A. Mann and M. Revzen, Thermal coherent states and thermal squeezed states, J. Mod. Opt., 1991, VOL . 38, 2339-2347
- ↑ G. J. Hyland, G. Rowlands, and F. W. Cummings, A proposal for an experimental determination of the equilibrium condensate fraction in superfluid helium, Phys. Lett. 31A (1970) 465-466.
- ↑ J. Mayers, The Bose–Einstein condensation, phase coherence, and two-fluid behavior in He-4, Phys. Rev. Lett. 92 (2004) 135302.
- ↑ J. Mayers, The Bose–Einstein condensation and two-fluid behavior in He-4, Phys. Rev. B 74 (2006) 014516.
- ↑ A.C. Olinto, Condensate fraction in superfluid He-4, Phys. Rev. B 35 (1986) 4771-4774
- ↑ O. Penrose and L. Onsager, Bose–Einstein condensation and liquid Helium, Phys. Rev. 104(1956) 576-584.
- ↑ C. N. Yang, Concept of Off-Diagonal Long-Range Order and the quantum phases of liquid He and superconductors, Rev. Mod Phys. 34 (1962) 694-704.
- ↑ Yang, C. N. (1962) Concept of off-diagonal long-range order and the quantum phases of liquid He and of superconductors. Reviews of Modern Physics, 34(4), 694.
- ↑ A. M. Perelomov, Coherent states for arbitrary Lie groups, Commun. Math. Phys. 26 (1972) 222-236; arXiv: math-ph/0203002 [Архівовано 23 Червня 2020 у Wayback Machine.].
- ↑ A. Perelomov, Generalized coherent states and their applications, Springer, Berlin 1986.
- ↑ R. Gilmore, Geometry of symmetrized states, Ann. Phys. (NY) 74 (1972) 391-463.
- ↑ R. Gilmore, On properties of coherent states, Rev. Mex. Fis. 23 (1974) 143-187.
- ↑ G. Kaiser, Quantum Physics, Relativity, and Complex Spacetime: Towards a New Synthesis, North-Holland, Amsterdam, 1990.
- ↑ S.T. Ali, J-P. Antoine, and J-P. Gazeau, Coherent States, Wavelets and Their Generalizations, Springer-Verlag, New York, Berlin, Heidelberg, 2000.
- ↑ C. Anastopoulos, Generalized Coherent States for Spinning Relativistic Particles, J. Phys. A: Math. Gen. 37 (2004) 8619-8637
- ↑ A. Ashtekar, J. Lewandowski, D. Marolf, J. Mourão and T. Thiemann, Coherent state transforms for spaces of connections, J. Funct. Anal. 135 (1996) 519-551.
- ↑ H. Sahlmann, T. Thiemann and O. Winkler, Coherent states for canonical quantum general relativity and the infinite tensor product extension, Nucl. Phys. B 606 (2001) 401-440.










![{\displaystyle \left[{X},{P}\right]\equiv {XP}-{PX}={\frac {i}{2}}\,{I}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e35bac8ea4ffc007e45e074a2dbe8ce0b7240308)















![{\displaystyle ~\psi ^{(\alpha )}(x,t)=\left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}e^{-{\frac {m\omega }{2\hbar }}\left(x-{\sqrt {\frac {2\hbar }{m\omega }}}\Re [\alpha (t)]\right)^{2}+i{\sqrt {\frac {2m\omega }{\hbar }}}\Im [\alpha (t)]x+i\theta (t)}~,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3efcf4e45d4b8cabae301d58f4fc5551ea0e5876)


![{\displaystyle \langle {\hat {x}}(t)\rangle ={\sqrt {\frac {2\hbar }{m\omega }}}\Re [\alpha (t)]=|\alpha (0)|{\sqrt {\frac {2\hbar }{m\omega }}}\cos(\sigma -\omega t)~,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36fb28403c8a64a8c127d31272cbad03998d553a)
![{\displaystyle \langle {\hat {p}}(t)\rangle ={\sqrt {2m\hbar \omega }}\Im [\alpha (t)]=|\alpha (0)|{\sqrt {2m\hbar \omega }}\sin(\sigma -\omega t)~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4956870f5290bff7024214ceb840926edd1e73ed)










![{\displaystyle |\alpha ,n\rangle =[{{\hat {a}}^{\dagger }]}^{n}|\alpha \rangle /\|[{{\hat {a}}^{\dagger }]}^{n}|\alpha \rangle \|~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eac570439ba5abbe376f835d59aee705c7760239)































