Кваркова модель

Рисунок 1: Псевдоскалярний нонет мезонів. Члени оригінального октету мезонів позначені зеленим кольором, а синглет — пурпуровим. Хоча нині ці мезони згруповані в нонет, назва «восьмикратного шляху» походить від груп восьми мезонів (та 8 баріонів) у першій запропонованій класифікації.

У фізиці елементарних частинок кваркова модель є схемою класифікації адронів з точки зору їх валентних кварків — кварків та антикварків, які породжують квантові числа адронів. Кваркова модель має в своїй основі симетрію «аромату SU(3)», та побудована на основі «вісімкового шляху» — успішної схеми класифікації, що охоплює велику кількість легших адронів, які були відкриті починаючи з 1950-х і продовжуючи до 1960-х років. Кваркова модель витримала експериментальну перевірку, починаючи з кінця 1960-х років, і є чинною класифікацією на сьогоднішній день. Модель була незалежно запропонована фізиками Мюрреєм Гелл-Манном який назвав частинки «кварками», та Джорджем Цвейгом, який запропонував термін «тузів». Кваркова модель наразі є компонентом усталеної квантової теорії поля сильних та електрослабких взаємодій елементарних частинок, що отримала назву Стандартна модель фізики елементарних частинок.

Адрони насправді не є «елементарними», і їх можна розглядати як зв'язані стани їх «валентних кварків» та антикварків, що породжують квантові числа адронів. Ці квантові числа є мітками, що ідентифікують адрони, і бувають двох видів. Один набір квантових чисел походить від симетрії Пуанкаре — J ^PC, де J, P та C означають повний кутовий момент (спін) адрона, P-симетрію та C-симетрію відповідно.

Іншими квантовими числами є квантові числа аромату, такі як ізоспін, дивність, чарівність тощо. Сильні взаємодії, що зв'язують кварки, нечутливі до цих квантових чисел, тому їх варіація призводить до систематичних взаємозв'язків маси та зв'язків між адронами в мультиплеті одного аромату.

Усім кваркам присвоєно баріонне число ⅓. Кварки u, c та t мають позитивний електричний заряд + ⅔, тоді як кварки d, s та b — негативний заряд, −⅓. Антикварки мають протилежні квантові числа. Кварки мають спін 1/2, а отже є ферміонами .

Мезони складаються з валентної пари кварк-антикварк (таким чином, мають баріонне число 0), тоді як баріони складаються з трьох кварків (таким чином, мають баріонне число 1). У цій статті розглядається кваркова модель для u, d і s ароматів кварків (які утворюють приблизну симетрію SU(3) аромату). Саме для цих трьох ароматів була запропонована первісна кваркова модель. Після відкриття трьох інших кварків (c, b, t) модель була узагальнена для більшої кількості ароматів.

Історія

Розробка схем класифікації адронів стала актуальним питанням після того, як нові експериментальні методи виявили так багато адронів, що стало зрозуміло, що всі вони не можуть бути елементарними. Це розмаїття навіть отримало назву «зоопарк частинок» (Particle Zoo). Ці відкриття змусили Вольфганга Паулі вигукнути: «Якби я міг таке передбачити, я пішов би в ботаніку», а Енріко Фермі порадив своєму студенту Леону Ледерману: «Юначе, якби я міг запам'ятати назви цих частинок, я був би ботаніком». Ці відкриття принесли Нобелівські премії фізикам-експериментаторам, зокрема Луїсу Альваресу, який був на чолі багатьох з цих розробок.

Побудова адронів як пов'язаних станів певних менших частинок, таким чином, могла б організувати відповідний «зоопарк». Кілька ранніх пропозицій, таких як моделі Енріко Фермі та Чен-Нін Ян (1949), і модель Саката (1956), в кінцевому підсумку задовільно охоплювали мезони, але зазнали невдачі з баріонами, тому не змогли пояснити всі дані.

Формула Гелл-Манна — Нішідзіми, розроблена Мюрреєм Гелл-Манном та Кадзухіко Нісідзімою, призвела до класифікації Вісімкового шляху, винайденої Гелл-Манном, з важливими незалежними внесками Юваля Неемана, в 1961 році. Адрони були організовані в симетрію SU(3), що представляла мультиплети — октети та декуплети — частинок приблизно однакової маси, і менші відмінності в масі, пов'язані із квантовими числами аромату, невидимі для сильних взаємодій. Формула маси Гелла-Манна — Окубо систематизувала кількісне визначення цих невеликих різниць маси серед представників адронного мультиплета, контрольованого явним порушенням симетрії SU(3).

Ключовим передбаченням кваркової моделі був Ω⁻
-баріон, який мав мати спін 3/2 та бути останнім членом декуплету баріонів. Після того, як його було виявлено в експерименті в Брукхейвенській національній лабораторії, Гелл-Манн отримав Нобелівську премію з фізики за свою роботу в 1969 році.

Нарешті, в 1964 р. Гелл-Манн і, незалежно від цього, Джордж Цвайг, розібралися, що насправді кодує картина «Вісімкового шляху». Вони запропонували три елементарні ферміони — u, d та s кварки — які не спостерігаються у вільній формі. Комбінації цих трьох складових та їх античастинок у парах чи трійках давали можливість пояснити всі відомі на той час адрони. Адронні відмінності у масі тепер були пов'язані з різними масами складових кварків.

Кваркова модель отримала загальне визнання лише за 10 років, після відкриття J/ψ-мезона, що у кварковій моделі лего пояснювався як зв'язаний стан нового c-кварка та його антикварка. Властивості цього мезона неможливо було пояснити жодною альтернативною моделлю. Основним джерелом протиріч був той факт, що кварки ніколи не можна спостерігати ізольовано (обмеження конфайнменту кольору). У наш час, кварки є базовим блоком квантової хромодинаміки, фундаментальної теорії, що повністю описує сильні взаємодії; а «вісімковий шлях» тепер розуміється як наслідок структури симетрії аромату трьох найлегших кварків.

Мезони

Рисунок 2: Псевдоскалярні мезони спіна 0 утворюють нонет

Малюнок 3: Мезони спіна 1 утворюють нонет

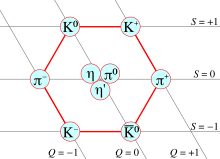
Класифікація «вісімкового шляху» названа за наступним фактом: якщо взяти три аромати кварків, то кварки лежать у фундаментальному представленні, 3 (так званому триплеті) симетрії аромату SU(3) . Антикварки лежать у комплексно-спряженому представленні 3. Дев'ять станів (нонет), складені з пари кварк-антикварк, можуть бути розкладені на тривіальне представлення, 1 (яке називається синглетом), і приєднане представлення, 8 (яке називається октетом). Стандартним позначенням цього розкладання є

$\mathbf {3} \otimes \mathbf {\overline {3}} =\mathbf {8} \oplus \mathbf {1}$ .

На рисунку 1 показано застосування цього розкладу до мезонів. Якби симетрія аромату була точною (як у умовній межі, де діють лише сильні взаємодії, але електрослабкі взаємодії умовно вимкнені), то всі дев'ять мезонів мали б однакову масу. Однак насправді треба враховувати порушення симетрії, спричинене різницею у масах кварків, та можливе змішування між різними мультиплетами (такими як октет та синглет).

Мезони мають нульове значення кольору (є колір-синглетом) — відтак, кварк та антикварк мають мати однаковий колір, але протилежний за знаком. Суперпозиція можливих станів кольору кварків (R, G, B — синій, зелений, червоний), та антикварків (анти-синій, анти-зелений, анти-червоний) дає

$\psi _{color}^{singlet}={\frac {1}{\sqrt {3}}}\left(R{\bar {R}}+B{\bar {B}}+G{\bar {G}}\right)$.

Відкритим питанням у кварковій моделі є пояснення великої різниці мас між η та η′ мезонами. Сучасна квантова хромодинаміка пояснює цю різницю топологічними особливостями вакууму сильної взаємодії, таких як конфігурації інстантону.

Мезони є адронами з нульовим баріонним числом. Якщо пара кварк-антикварк перебуває в стані з орбітальним моментом імпульсу L і має спін S, тоді

• |L — S| ≤ J ≤ L + S, де S = 0 (якщо спіни кварка та антикварка різнонаправлені) або 1 (якщо спіни направлені в один бік);
• P = (−1)^L+1, де 1 в показнику походить від власної парності пари кварк-антикварк.
• C = (–1)^L+S для мезонів, які не мають аромату (тобто складаються з кварка та антикварка одного аромату). Мезони з ненульовим ароматом не мають визначеного значення С.
• Для станів з ізоспіном I = 1 та 0 можна визначити нове мультиплікативне квантове число, яке називається G-парність, таке, що G = (−1)^{I + L + S}.

Якщо P = (–1)^J (так звана «натуральна парність», $J^{P}=0^{+},1^{-},2^{+}$ тощо), тоді S = 1, отже, PC = +1. Таким чином, можуть існувати стани з $J^{PC}=0^{++},1^{--},2^{++},3^{--}$тощо.

Якщо ж P = (–1)^J+1 (так звана «ненатуральна парність», $J^{P}=0^{-},1^{+},2^{-}$ тощо), тоді дозволені не лише квантові стани $J^{PC}=0^{-+},1^{++},2^{-+},3^{++}$ тощо, але й $J^{PC}=1^{+-},2^{--},3^{+-}$ тощо.

Усі інші квантові стани (наприклад, стан $J^{PC}=0^{--}$, або стани з $J^{PC}=0^{+-},1^{-+},2^{+-}$ тощо з P = (–1)^J, але PC = –1) не можуть бути сформовані в моделі кварк-антикварк, та називаються екзотичними. Мезони з такими квантовими числами мусять мати складнішу структуру — наприклад, бути тетракварками.

Баріони

Малюнок 4. Основні стани баріонів з S =  1/2 утворюють октет.

Малюнок 5. Баріони з S = 3/2 утворюють декуплет.

Оскільки кварки є ферміонами, теорема спінової статистики (принцип Паулі) передбачає, що хвильова функція баріона повинна бути антисиметричною при перестановці будь-яких двох кварків.

При цьому, можна записати хвильову функцію як добуток її частин, залежних від кольору, аромату, спіну та просторових координат:

$\psi =\psi _{color}\times \psi _{spin}\times \psi _{flavor}\times \psi _{spatial}$

Хвильова функція баріона визначається тим фактом, що баріони мають нульовий колір (є колір-синглетом) — відтак, усі три кварки мусять мати різний колір. Суперпозиція можливих станів кольору кварків (R, G, B — синій, зелений, червоний) дає

$\psi _{color}^{singlet}={\frac {1}{\sqrt {6}}}\left(RGB-RBG+BRG-BGR+GBR-GRB\right)$

Ця комбінація є повністю антисиметричною за кольором, оскільки змінює знак при перестановці будь-якої пари кварків.

Через це, для отримання антисиметричної повної хвильової функції баріона, вона має бути симетричною за ароматом, спіном та простором взятими разом. З трьома ароматами, розкладання за ароматом можна записати як

$\mathbf {3} \otimes \mathbf {3} \otimes \mathbf {3} =\mathbf {10} _{S}\oplus \mathbf {8} _{M}\oplus \mathbf {8} _{M}\oplus \mathbf {1} _{A}$ .

Хвильова функція членів декуплета є симетричною за ароматом, синглета — антисиметрична, а два октети мають змішану симетрію.

Просторова частина хвильової функції фіксується, коли задано орбітальний кутовий момент: для прикладу, в основному стані (орбітальний момент $L=0$) просторова частина хвильової функції, пропорційна $(-1)^{L}$, є симетричною.

Іноді корисно розглядати кварки як шість станів із трьома ароматами та двома спінами на аромат. Ця наближена симетрія спіну-аромату називається SU(6). З точки зору цієї симетрії, розкладання є

$\mathbf {6} \otimes \mathbf {6} \otimes \mathbf {6} =\mathbf {56} _{S}\oplus \mathbf {70} _{M}\oplus \mathbf {70} _{M}\oplus \mathbf {20} _{A}~.$

56 станів із симетричним поєднанням спіна та аромату розкладаються під ароматом SU(3) на

$\mathbf {56} =\mathbf {10} ^{\frac {3}{2}}\oplus \mathbf {8} ^{\frac {1}{2}}~,$

де верхній індекс позначає спін S баріона. Оскільки ці стани симетричні за спіном та ароматом, вони також повинні бути симетричними в просторі — умова, яка легко задовольняється, якщо орбітальний момент руху L = 0. Це баріони основного стану.

Октет баріонів з S=1/2 представлений двома нуклонами ( p⁺
, n⁰
), трьома Сигма-баріонами ( Σ⁺
, Σ⁰
, Σ⁻
), двома Ксі-баріонами ( Ξ⁰
, Ξ⁻
), і Лямбда-баріоном ( Λ⁰
). Декуплет баріонів зі спіном S=3/2 містить чотири Дельта-баріони ( Δ⁺⁺
, Δ⁺
, Δ⁰
, Δ⁻
), три збуджених Сигма-баріони ( Σ^∗+
, Σ^∗0
, Σ^∗−
), два збуджених Ксі-баріони ( Ξ^∗0
, Ξ^∗−
), і Омега-баріон ( Ω⁻
).

Наприклад, хвильова функція спіну-аромату для протона має вигляд

$|p_{\uparrow }\rangle ={\frac {1}{\sqrt {18}}}[2|u_{\uparrow }d_{\downarrow }u_{\uparrow }\rangle +2|u_{\uparrow }u_{\uparrow }d_{\downarrow }\rangle +2|d_{\downarrow }u_{\uparrow }u_{\uparrow }\rangle -|u_{\uparrow }u_{\downarrow }d_{\uparrow }\rangle -|u_{\uparrow }d_{\uparrow }u_{\downarrow }\rangle -|u_{\downarrow }d_{\uparrow }u_{\uparrow }\rangle -|d_{\uparrow }u_{\downarrow }u_{\uparrow }\rangle -|d_{\uparrow }u_{\uparrow }u_{\downarrow }\rangle -|u_{\downarrow }u_{\uparrow }d_{\uparrow }\rangle ].$

Кваркова модель успішно передбачає різниці мас між баріонами всередині одного мультиплета та між мультиплетами, а також магнітні моменти баріонів.

Відкриття кольору

Квантове число кольору є характерним зарядом сильної взаємодії і абсолютно не бере участі в електрослабких взаємодіях. Воно було запропоноване як наслідок класифікації кваркової моделі, коли було зрозуміло, що для баріона з S=3/2, Δ⁺⁺
(кварковий склад $uuu$), потрібні три u-кварки з паралельними спінами (щоб утворити загальний спін 3/2) та нульовим орбітальним кутовим моментом. Такий баріон не міг би мати антисиметричну хвильову функцію (вимагається принципом виключення Паулі), якби не існувало ще одного квантового числа. Оскар Грінберг припустив у 1964 році, що кварки можуть бути параферміонами.

Натомість за півроку Му-Янг Хань та Йоїчіро Намбу запропонували існування трьох триплетів кварків, щоб вирішити цю проблему, але аромат і колір перепліталися в цій моделі: вони не комутували.

Сучасна концепція кольору, що повністю комутує з усіма іншими зарядами та забезпечує сильну взаємодію, була сформульована в 1973 році Вільямом Бардіном, Харальдом Фріцшем та Мюрреєм Гелл-Манном.

Частинки поза кварковою моделлю

Хоча кваркова модель випливає з теорії квантової хромодинаміки, структура реальних адронів є більш складною. Повна квантово-механічна хвильова функція будь-якого адрону повинна включати віртуальні пари кварків, а також віртуальні глюони, і дозволяє різноманітні змішування квантових станів.

Можуть існувати адрони, які лежать поза моделлю кварків. Серед них — глюболи (що містять лише валентні глюони), гібриди (які містять валентні кварки, а також глюони) та «екзотичні адрони» (наприклад, тетракварки або пентакварки).

Див. також

• Субатомні частинки
• Адрони, баріони, мезони та кварки
• Кварконій
• Квантова хромодинаміка

Список літератури

• S. Eidelman et al. Particle Data Group (2004). Review of Particle Physics (PDF). Physics Letters B. 592 (1–4): 1. arXiv:astro-ph/0406663. Bibcode:2004PhLB..592....1P. doi:10.1016/j.physletb.2004.06.001. Архів оригіналу (PDF) за 3 Березня 2016. Процитовано 24 Лютого 2021.
• Lichtenberg, D B (1970). Unitary Symmetry and Elementary Particles. Academic Press. ISBN 978-1483242729.
• Томсон, Массачусетс (2011), Конспект лекцій [Архівовано 5 Липня 2016 у Wayback Machine.]
• J.J.J. Kokkedee (1969). The quark model. W. A. Benjamin. ASIN B001RAVDIA.