Дискретна математика
| Ця стаття містить правописні, лексичні, граматичні, стилістичні або інші мовні помилки, які треба виправити. |
Дискре́тна матема́тика — галузь математики, що вивчає властивості будь-яких дискретних структур. Як синонім іноді вживається термін дискре́тний ана́ліз, що вивчає властивості структур скінченного характеру. До таких структур може бути віднесено скінченні групи, скінченні графи, а також деякі математичні моделі перетворювачів інформації, скінченні автомати, машини Тюрінга тощо. Розділ дискретної математики, що вивчає їх, називається скінче́нною матема́тикою. Іноді саме це поняття розширюють до дискретної математики. Крім вказаних скінченних структур, дискретна математика вивчає деякі системи алгебри, нескінченні графи, обчислювальні схеми певного вигляду, клітинні автомати тощо.
Історія дискретної математики[ред. | ред. код]

Історія дискретної математики пов'язана з розв'язанням складних проблем, які привернули увагу в цій області. В теорії графів багато досліджень було викликано спробами довести теорему чотирьох кольорів, вперше сформульовану 1852 року, але не доведену до 1976 (Кеннет Аппель і Вольфганг Хакен — довели використовуючи суттєву допомогу комп'ютера).
У логіці прикладом таких задач є друга проблема зі списку Давида Гільберта, який був представлений в 1900 році. В ній йдеться про доведення, що арифметичні аксіоми є несуперечливими. Друга теорема Геделя про неповноту формалізованої арифметики, доведена 1931 року, показала, що це довести неможливо — принаймні, в межах арифметики. Десята проблема Гільберта повинна була визначити, чи має дане діофантове рівняння цілі коефіцієнти та цілі рішення. У 1970 році Юрій Матіясевич довів, що цього не може бути.
Необхідність розкрити німецькі коди Другої світової війни призвела до досягнень в області криптографії та теоретичної інформатики, а також до появи першої програмованої цифрової електронної обчислювальної машини, розробленої в Англії. У той же час, військові вимоги мотивували досягнення в галузі дослідження операцій. Холодна війна означала, що криптографія залишалася важливою наукою з фундаментальними досягненнями, такими як шифрування з відкритим ключем, які розроблялися в наступних десятиліттях. Дослідження операцій залишається важливим розділом, як інструмент управління бізнесом і проєктами. Телекомунікаційна промисловість також спонукала прогрес у дискретній математиці, особливо в теорії графів та теорії інформації. Формальна перевірка тверджень в логіці була необхідною для розробки програмного забезпечення безпеково критичних систем[en].
В даний час однією з найвідоміших відкритих проблем в теоретичній інформатиці є P = NP проблема, яка включає в себе відношення між класами складності P та NP. Математичний інститут Clay запропонував приз $ 1 млн. USD за перше правильне доведення, поряд із призами для шести інших математичних проблем.
Теоретична інформатика[ред. | ред. код]
Теоретична інформатика включає в себе області дискретної математики, що мають відношення до обчислень. В значній мірі вона спирається на теорію графів та логіку. В межах теоретичної інформатики вивчаються алгоритми для обчислення математичних результатів. Обчислюваність вивчає, які задачі можуть бути обчислені в принципі, і близько пов'язана з логікою, а складність визначає час, якого ці обчислення потребують. Теорія автоматів і теорія формальної мови близько пов'язані з обчислюваністю. Мережі Петрі та числення процесів використовуються при моделюванні обчислювальних систем, а методи дискретної математики використовуються в аналізі електричних схем VLSI.
При вирішенні геометричних задач застосовують алгоритми обчислювальної геометрії, тоді як до представлення зображень використовують дискретний аналіз комп'ютерного зображення. Теоретична інформатика також включає вивчення різних неперервних обчислювальних тем.
Теорія інформації[ред. | ред. код]
Теорія інформації — це розділ кібернетики, в якому за допомогою математичних методів вивчаються способи вимірювання інформації та методи її кодування з метою стиснення і надійної передачі каналами зв'язку.

При формальному поданні знань кожному досліджуваному об'єктові ставиться у відповідність числовий код, зв'язки між об'єктами так само подаються кодами. Для переведення неформальних даних до формального цифрового вигляду застосовуються спеціальні таблиці кодування. Найпростіший приклад такої таблиці — ASCII (American Standard Code for Information Interchange), що керує символами чисел від 0 до 127.
Інформація може бути двох видів: дискретна (цифрова) та неперервна (аналогова). Неперервна інформація — це дані, що одержані при неперервному за часом процесі змінювання деякої випадкової величини і описуються неперервними (аналоговими) функціями.
Дискретна інформація — це цифрові дані, одержані в результаті квантування (дискретизації) неперервної величини за часом, рівнем або тим і іншим одночасно. Дискретну інформацію зберігати й обробляти набагато простіше, оскільки вона являє собою послідовність чисел. У двійковій системі числення дискретна інформація являє собою послідовність 0 та 1.
Логіка[ред. | ред. код]
Математична логіка (теоретична логіка, символічна логіка) — розділ математики, що вивчає докази і питання підстав математики. «Предмет сучасної математичної логіки різноманітний.»[на чию думку?]. Відповідно до визначення П. С. Порецького, «математична логіка є логіка по предмету, математика за методом». Відповідно до визначення Н. І. Кондакова, «математична логіка — друга, після традиційної логіки, щабель у розвитку формальної логіки, що застосовує математичні методи та спеціальний апарат символів і досліджує мислення за допомогою числень (формалізованих мов).» Це визначення відповідає визначенню С. К. Кліні: математична логіка — це «логіка, що розвивається за допомогою математичних методів». Також А. А. Марков визначає сучасну логіку «точною наукою, яка застосовує математичні методи». Всі ці визначення не суперечать, а доповнюють одне одного.
Застосування в логіці математичних методів стає можливим тоді, коли судження формулюються деякою точною мовою. Такі точні мови мають дві сторони: синтаксис і семантику. Синтаксисом називається сукупність правил побудови об'єктів мови (зазвичай званих формулами). Семантикою називається сукупність угод, що описують наше розуміння формул (або деяких з них) і дозволяють вважати одні формули вірними, а інші — ні.
Важливу роль в математичній логіці мають поняття дедуктивної теорії та обчислення. Обчисленням називається сукупність правил виводу, що дозволяють вважати деякі формули виведеними. Правила виведення поділяються на два класи. Одні з них безпосередньо кваліфікують деякі формули як виведені. Такі правила виведення прийнято називати аксіомами. Інші ж дозволяють вважати виведеними формули , синтаксично пов'язані деяким заздалегідь певним способом з кінцевими наборами виведених формул. Широко застосовуваним правилом другого типу є правило modus ponens: якщо виведено формули , то виводиться й формула .
Відношення числень до семантики виражається поняттями семантичної придатності та семантичної повноти обчислення. Обчислення О називається семантично придатним для мови М, якщо будь-яка вивідна в О формула мови М є вірною. Аналогічно, обчислення О називається семантично повним в мові Я, якщо будь-яка вірна формула мови М є вивідною в О.
Математична логіка вивчає логічні зв'язки та відношення, що лежать в основі логічного (дедуктивного) виводу з використанням мови математики.
Багато які з розглянутих в математичній логіці мов мають семантично повні й семантично придатні обчислення. Зокрема, відомий результат К. Геделя про те, що так зване класичне числення предикатів є семантично повним і семантично придатним для мови класичної логіки предикатів першого порядку. З іншого боку, є чимало мов, для яких побудова семантично повного і семантично придатного обчислення неможливе. В цій області класичним результатом є теорема Геделя про неповноту, яка стверджує неможливість семантично повного й семантично придатного числення для мови формальної арифметики.
Варто зазначити, що на практиці множина елементарних логічних операцій є обов'язковою частиною набору інструкцій всіх сучасних мікропроцесорів, і відповідно входить до мови програмування. Це є одним з найважливіших практичних додатків методів математичної логіки, що вивчаються в сучасних підручниках інформатики.
Теорія множин[ред. | ред. код]
В основі теорії множин лежать первинні поняття: множина та елемент множини. Елемент множини перебуває щодо множини у відношенні бути елементом множини (позначається як [2] — «x є елемент множини A»). Серед похідних понять найважливішими є наступні:
- порожня множина — множина, яка не містить елементів, позначається зазвичай ;
- підмножина і надмножина — множина, яка складається тільки з елементів іншої множини, та множина, до якої належать усі елементи іншої множини, відповідно;
- сімейство множин;
- простір (універсум) — множина, що є надмножиною всіх множин;
- конституента.
Над множинами визначено наступні операції:
- об'єднання (або сума) (позначається як );
- перетин (або добуток) (позначається як );
- різниця (позначається як рідше );
- симетрична різниця (позначається як рідше ).
- доповнення (позначається як або );
Для множин визначено наступні бінарні відношення:
- відношення рівності (позначається як );
- відношення включення (позначається як або ).
Комбінаторика[ред. | ред. код]
Комбінато́рика (комбінаторний аналіз) — розділ математики, присвячений розв'язанню задач вибору та розташування елементів деякої, зазвичай скінченної, множини відповідно до заданих правил. Кожне таке правило визначає спосіб побудови деякої конструкції із елементів вихідної множини, що зветься комбінаторною конфігурацією. Тому на меті комбінаторного аналізу стоїть дослідження комбінаторних конфігурацій, алгоритмів їх побудови, оптимізація таких алгоритмів, а також розв'язання задач переліку.
Найпростішими прикладами комбінаторних конфігурацій є перестановки, розміщення, комбінація та розбиття.
Комбінаторика пов'язана з багатьма іншими розділами математики. Термін «комбінаторика» ввів Лейбніц, який у 1666 році опублікував свою працю «Міркування про комбінаторне мистецтво». Іноді під комбінаторикою розуміють ширший розділ дискретної математики, що включає теорію графів.
Приклади комбінаторних конфігурацій і задач[ред. | ред. код]
Для формулювання та розв'язання комбінаторних задач використовують різні моделі комбінаторних конфігурацій. Прикладами комбінаторних конфігурацій є:
- Розміщення з елементів по — упорядкований набір з різних елементів деякої -елементної множини;
- Перестановка з елементів (наприклад чисел ) — всякий упорядкований набір з цих елементів. Перестановка також є розміщенням з елементів по ;
- Поєднання з по — набір елементів, вибраних з даних елементів. Набори, що відрізняються тільки порядком проходження елементів (але не складом), вважаються однаковими, цим поєднання відрізняється від розміщення;
- Композиція числа — всяке представлення у вигляді впорядкованої суми цілих додатних чисел;
- Розбиття числа — всяке представлення у вигляді невпорядкованою суми цілих додатних чисел.
Прикладами комбінаторних завдань є:
- Скількома способами можна розмістити предметів в скриньках так, щоб виконувалися задані обмеження?
- Скільки існує функцій з -елементної множини в -елементній, що задовольняють заданим обмеженням?
- Скільки існує різних перестановок з гральних карт?
- Відповідь: ( факторіал), тобто, або приблизно 8,0658 × 1067.
- При грі в кості кидаються два кубики, і кількість очок, що випали, складаються; скільки існує таких комбінацій, що сума очок на верхніх гранях дорівнює дванадцяти?
- Рішення: Кожен можливий результат відповідає функції (Аргумент функції — це номер кубика, значення — число на верхній грані). Очевидно, що лише дає потрібний результат . Таким чином існує лише одна функція, яка ставить у відповідність 1 число , і число . Або, іншими словами, існує лише одна комбінація, така, що сума очок на верхніх гранях дорівнює дванадцяти.
Теорія графів[ред. | ред. код]

Теорія графів — розділ дискретної математики, що вивчає властивості графів. У загальному значенні граф подається як множина вершин (вузлів), з'єднаних ребрами. У строгому визначенні графом називається така пара множин , де V є підмножина будь-якої числової множини, а E — підмножина .
Теорія графів має застосування, наприклад, в геоінформаційних системах (ГІС). Побудовані або спроєктовані будинки, споруди, квартали тощо розглядаються як вершини, поєднані дорогами, інженерними мережами, лініями електропередач тощо — як ребра. Застосування різних обчислень на такому графі, дозволяє, наприклад, знайти найкоротший об'їзний шлях або найближчий продуктовий магазин, спланувати оптимальний маршрут.
Родоначальником теорії графів вважається Леонард Ейлер. У 1736 році в одному зі своїх листів він формулює і пропонує рішення задачі про сім Кеніґсберських мостів, що стала згодом однією з класичних задач теорії графів.
Термінологія теорії графів понині строго не визначена. Зокрема, в монографії «Введення в розробку та аналіз алгоритмів» Гудман та Хідетніемі, 1977, сказано: «У світі програмістів немає єдиної думки про те, який з двох термінів „граф“ або „мережа“ краще використовувати. Ми вибрали термін „мережа“, так як він, мабуть, частіше зустрічається у прикладних областях. Аналогічна ситуація для „вершина / точка“».[3]
При зображенні графів найчастіше використовується наступна система позначень: кожній вершині зіставляється точка на площині, і якщо між вершинами існує ребро, то відповідні точки з'єднуються відрізком. У разі орієнтованого графу відрізки замінюють стрілками.
Не слід плутати зображення графу із власне графом (абстрактною структурою), оскільки одному графу можна зіставити не одне графічне представлення. Зображення покликане лише показати, які пари вершин з'єднані ребрами, а які — ні. Часто на практиці буває важко відповісти на питання, чи є два зображення моделями одного і того ж графу чи ні. Залежно від завдання, одні зображення можуть давати більш наочну картину, ніж інші.
Теорія графів містить велику кількість невирішених проблем і поки не доведених гіпотез.[яких?]
Ймовірності[ред. | ред. код]
Ймові́рність (лат. probabilitas, англ. probability) — числова характеристика можливості того, що випадкова подія відбудеться в умовах, які можуть бути відтворені необмежену кількість разів. Імовірність є основним поняттям розділу математики, що називається теорія імовірностей.
Випадковою подією називається подія, результат якої не може бути відомий наперед. Навіть у тому разі, коли насправді подія детермінована своїми передумовами, вплив цих передумов може бути настільки складним, що вивести з них наслідок логічно й послідовно, неможливо. Наприклад, при підкидуванні монети, сторона на яку монета впаде визначається положенням руки і монети в руці, швидкістю, обертовим моментом тощо, однак відслідкувати всі ці фактори неможливо, тому результат можна вважати випадковим.
Існують два підходи до означення імовірності: математично-аксіоматичний і Баєсів. Аксіоматичний підхід, строго сформульований Колмогоровим, будується на припущенні, що імовірності елементарних випадкових подій задані, і зосереджується на визначенні ймовірностей складних подій, що є сукупністю елементарних. Так, наприклад, при підкидуванні шестигранного кубика гральної кості, ймовірності випадіння будь-якого числа, вважаються однаковими й рівними 1/6. Виходячи з цієї аксіоми, теорія ймовірності може розрахувати ймовірність того, що сума чисел на двох костях буде, наприклад, 8.
Баєсів підхід не робить припущень про ймовірності елементарних подій, а намагається отримати їх із аналізу попереднього досвіду, спираючись на теорему Баєса і на попередні гіпотези. Баєсів підхід ближчий до того, як визначаються імовірності випадкових подій у природознавстві. Оскільки ці ймовірності наперед невідомі, результати серії дослідів розбиваються на сприятливі й несприятливі, і експериментально визначена ймовірність дорівнює відношенню числа сприятливих подій до числа дослідів, тобто частоті подій.
Надалі в цій статті використовується аксіоматичний математичний підхід.
Означення[ред. | ред. код]
Нехай Ω = {ω1, ω2 , … , ωn} — простір елементарних подій. Припустімо, що кожній елементарній події ωk можна поставити у відповідність невід'ємне число pk (імовірність події ωk), причому .
Якщо — випадкова подія і , то
- ,
де називається імовірністю події .
Визначення термінів[ред. | ред. код]
- Умовна імовірність — імовірність події B, вирахувана в припущенні, що подія А вже відбулася;
- Несумісні події — дві випадкові події, якщо вони не можуть відбутися одночасно. Якщо події А та В несумісні, то ;
- Повна група подій — система випадкових подій така, що в результаті проведеного випадкового експерименту неодмінно станеться одне з них.
Властивості[ред. | ред. код]
- Імовірність достовірної події дорівнює 1;
- Імовірність неможливої події дорівнює 0;
- Імовірність випадкової величини є позитивним числом, що міститься між нулем та одиницею:
Теорія чисел[ред. | ред. код]
Теорія чисел або вища арифметика — розділ математики, що вивчає цілі числа і подібні об'єкти. Залежно від використовуваних методів теорію чисел поділяють на кілька підтеорій.
1) Елементарна теорія чисел У елементарної теорії чисел цілі числа вивчаються без використання методів інших розділів математики. Такі питання, як подільність цілих чисел, алгоритм Евкліда для обчислення найбільшого спільного дільника і найменшого спільного кратного, розкладання числа на прості множники, побудова магічних квадратів, досконалі числа, числа Фібоначчі, мала теорема Ферма, теорема Ейлера, задача про чотири куби відносяться до цього розділу.
2) Аналітична теорія чисел В аналітичній теорії чисел для виводу і доказів тверджень про числа та числові функції використовується потужний апарат математичного аналізу. Велику роль в аналітичній теорії чисел грає метод тригонометричних сум, що дозволяє оцінювати кількість розв'язків тих чи інших рівнянь або систем рівнянь у цілих числах. Основи методу тригонометричних сум розробив і вперше застосував до завдань теорії чисел І. М. Виноградов.
Першим успіхом аналітичної теорії чисел було застосування комплексного аналізу в доведенні теореми про розподіл простих чисел. Найбільш відомою і досі не вирішеною проблемою аналітичної теорії чисел є доказ гіпотези Рімана про нулі дзета-функції, яка стверджує, що всі нетривіальні корені рівняння лежать на так званій критичній прямій , Де — дзета-функція Рімана.
3) Алгебраїчна теорія чисел В алгебраїчній теорії чисел поняття числа розширюється, як алгебраїчні числа розглядають корені многочленів з раціональними коефіцієнтами. При цьому аналогом цілих чисел виступають цілі алгебраїчні числа, тобто корені унітарних многочленів з цілими коефіцієнтами. На відміну від цілих чисел, в кільці цілих алгебраїчних чисел не обов'язково виконується властивість факторіального, тобто єдиності розкладання на прості множники.
До алгебраїчної теорії чисел належать такі розділи, як теорія дивізорів, теорія Галуа, теорія полів класів, дзета- і L-функції Дирихле, когомологій груп і багато іншого. Одним з основних прийомів є вкладення поля алгебраїчних чисел свого поповнення в якийсь із метрик — Архімедова (наприклад, в поле речових або комплексних чисел) або неархімедовой (наприклад, у полі p-адіческіх чисел).
Алгебра[ред. | ред. код]
Є як дискретні, так і неперервні приклади алгебраїчних структур. До дискретної алгебри належать: булева алгебра, використовується в логічних вентилях і програмуванні; реляційна алгебра, використовується в базах даних; дискретні та скінченні групи, кільця і поля відіграють важливу роль в алгебраїчній теорії кодування; дискретні напівгрупи і моноїди з'являються в теорії формальних мов.
Дискретний аналіз[ред. | ред. код]
Дискретний аналіз — це сукупність математичних дисциплін, які можуть вивчатися та розвиватися як самостійні, незалежні теорії (хоча в будь-якому разі ці дисципліни є взаємопроникними та тісно переплітаються навіть при окремому вивченні кожної з них). Незважаючи на це, їх об'єднує дослідження явищ, що мають дискретний характер, або таких, що можуть бути приведені до дискретного виду для спрощення обчислень без втрати актуальності та належного ступеня точності. Необхідність вивчення дискретного аналізу стає більш зрозумілою, якщо врахувати, що практично всі соціально-економічні процеси є дискретними. Навіть якщо такий процес розвивається неперервно, то інформація потрапляє до дослідника дискретно. В дискретний аналіз зазвичай включають такі дисципліни: теорія множин, математична логіка, комбінаторний аналіз, теорія графів, теорія нечітких підмножин та чисельні методи.
Обчислення кінцевих різниць — кінцевою різницею функції від однієї або декількох змінних називається приріст функції при даних кінцевих прирости змінних незалежних. Під І. кінцевих різниць розуміють сукупність правил: для визначення змін, яким піддаються функції при кінцевих приростах змінних, що до них входять, і для визначення первісних функцій, коли змінені їх види відомі (прямий і зворотний способи). При першій появі диференціального обчислення прирощення змінних величин розглядалися як нескінченно малі величини, другими і вищими ступенями яких нехтували, внаслідок чого у багатьох з математиків з'явився сумнів у строгості самого способу і правильності результатів, одержуваних диференціальним численням. Щоб довести правильність нового способу, англійський математик Тейлор у творі «Methodus incrementorum Directa та ін Inversa», виданому в 1715 році, запропонував спосіб обчислення кінцевих різниць, в якому прирощення змінних розглядалися як кінцеві величини, вищими ступенями яких вже не можна нехтувати. Однак обчислення кінцевих різниць, що представляє по суті обчислення рядів, має, як зауважив Лагранж, мало спільного з диференціальним численням, предмет якого є обчислення похідних функцій. Перші сліди дослідження кінцевих різниць видно в деяких прийомах Фермата, Баррова і Лейбніца, але засновником способу, як самостійного обчислення, слід вважати Тейлора. Пізнішими дослідниками були Ніколь, Кондорсе, Емерсон, Ейлер, Лагранж і Лаплас. Вони удосконалили цю важливу галузь чистого аналізу і показали різні її додатки до інтерполяції і підсумовування рядів, до теорії з'єднань і особливо до теорії ймовірностей.
Геометрія[ред. | ред. код]

Обчислювальна геометрія (англ. computational geometry) — галузь комп'ютерних наук присвячена вивченню алгоритмів що описуюються в термінах геометрії.
Основним стимулом розвитку обчислювальної геометрії як дисципліни був прогрес у комп'ютерній графіці та системах автоматизованого проектування та автоматизованих систем технологічної підготовки виробництва, проте багато задач обчислювальної геометрії є класичними за своєю природою і можуть з'являтись при математичній візуалізації.
Іншим важливим застосуванням обчислювальної геометрії є робототехніка (планування руху та задачі розпізнавання образів), геоінформаційні системи (геометричний пошук, планування маршруту), дизайн мікросхем, програмування верстатів з числовим програмним керуванням.
Основними розділами обчислювальної геометрії є:
- Комбінаторна обчислювальна геометрія, чи також названа алгоритмічна геометрія, яка розглядає геометричні об'єкти як дискретні сутності;
- Чисельна обчислювальна геометрія, також названа машинна геометрія чи геометричне моделювання, яка має справу в основному з представленням об'єктів реального світу в формі, придатній для подальшої комп'ютерної обробки.
Топологія[ред. | ред. код]
Хоча топологія є областю математики, що формалізує та узагальнює інтуїтивне поняття «неперервної деформації» об'єктів, вона дає початок багатьом темам дискретної математики; це може бути приписано зокрема до центру на топологічних інваріантах, які безпосередньо зазвичай беруть дискретні значення. Є такі розділи, як комбінаторна топологія, топологічна теорія графів, топологічна комбінаторика, обчислювальна топологія, дискретний топологічний простір, обмежений топологічний простір, топологія (хімія).
Дослідження операцій[ред. | ред. код]
Дослідження операцій — це дисципліна, що займається розробкою й застосуванням методів знаходження оптимальних рішень на основі математичного моделювання у різних областях людської діяльності. дисципліна тісно пов'язана з системним аналізом, математичним програмуванням, теорією оптимальних рішень.
Дослідження операцій — застосування математичних, кількісних методів для обґрунтування рішень у всіх галузях цілеспрямованої людської діяльності. Дослідження операцій починається тоді, коли для обґрунтування рішень використовується той чи інший математичний апарат.[4]
Теорія ігор, теорія рішень, теорія корисності, теорія суспільного вибору[ред. | ред. код]
Теорія ігор[ред. | ред. код]
Теорія ігор — розділ прикладної математики, який використовується в соціальних науках (найбільше в економіці), біології, політичних науках, комп'ютерних науках (головним чином для штучного інтелекту) і філософії. Теорія ігор намагається математично зафіксувати поведінку в стратегічних ситуаціях, в яких успіх суб'єкта, що робить вибір залежить від вибору інших учасників.
Теорія ігор широко використовує різноманітні математичні методи і результати теорії ймовірностей, класичного аналізу, функціонального аналізу (особливо важливими є теореми про нерухомі точки), комбінаторної топології, теорії диференціальних та інтегральних рівнянь, та інші. Специфіка теорії ігор сприяє розробці різноманітних математичних напрямів (наприклад, теорія опуклих множин, лінійне програмування, і так далі).
Теорія рішень[ред. | ред. код]
Теорія рішень — розділ прикладної математики, який математичними методами досліджує закономірності вибору людьми найвигідніших із можливих альтернатив. Має застосування в економіці, менеджменті, когнитивній психології, інформатиці та обчислювальній техніці. Розрізняють нормативну теорію, яка описує раціональний процес вибору та дескриптивну теорію, що стосується практики вирішування.
Теорія рішень базується на шести аксіомах. Лотереєю називається гра з двома виходами: х із ймовірністю р та виходом у з імовірністю 1-р; символьний запис для лотереї: .
- Аксіома 1. Виходи х, у, z належать множині виходів.
- Аксіома 2. Нехай означає відношення нестрогої переваги, а — відношення байдужості (еквівалентності). Виконуються дві умови:
- зв'язності: ;
- транзитивності: з випливає .
- Аксіома 3. Лотереї і перебувають у відношенні байдужости.
- Аксіома 4. Якщо , то .
Теорія корисності[ред. | ред. код]
Теорія корисності — складова частина економічної теорії, яка прагне пояснити економічну поведінку раціонального індивіда через використання понять «корисність» та «максимізація корисності».
Теорія суспільного вибору[ред. | ред. код]
Теорія суспільного вибору — один з розділів економіки, що вивчає різні способи і методи, за допомогою яких люди використовують урядові установи у своїх власних інтересах.
Дискретизація[ред. | ред. код]
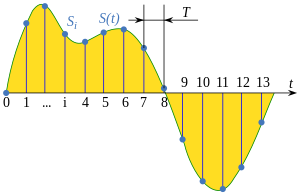
Дискретиза́ція — перетворення функцій неперервних змінних у функції дискретних змінних, за якими початкові неперервні функції можуть бути відновлені із заданою точністю. Роль відліків виконують квантовані значення функцій. Під квантуванням розуміють перетворення неперервної за значеннями величини у величину з дискретною шкалою значень з скінченної множини дозволених, які називають рівнями квантування. Якщо рівні квантування нумеровані, то результатом перетворення є число, яке може бути виражене в будь-якій системі числення.
Дискретні аналоги неперервної математики[ред. | ред. код]
Є багато концепцій в неперервній математиці, які мають дискретні версії, таких як дискретні обчислення, дискретний розподіл ймовірності, дискретні перетворення, дискретна геометрія, дискретні логарифми, дискретна диференціальна геометрія, дискретне зовнішнє обчислення, дискретні динамічні системи і дискретні векторні міри.
Література[ред. | ред. код]
Українською[ред. | ред. код]
- Базилевич Л. Є. Дискретна математика у прикладах і задачах : теорія множин, математична логіка, комбінаторика, теорія графів. — Математичний практикум. — Львів, 2013. — 486 с. — ISBN 9789662645095.
- Бондарчук Ю. В., Олійник Б. В. Основи дискретної математики. — Київ : Видавничий дім «Києво-Могилянська Академія», 2009. — 160 с. — ISBN 978-966-518-484-3.
- Вступ до дискретної математики / В. І. Андрійчук, М. Я. Комарницький, Ю. Б. Іщук; Львів. нац. ун-т ім. І.Франка. — Л., 2003. — 254 c. — Бібліогр.: 21 назв.
- Дискретна математика для програмістів: навч. посіб. / Л. М. Журавчак. — Львів: Львівська політехніка, 2019. — 420 с. — ISBN 966-941-325-3.
- Дискретна математика: Навч. посіб. для студ. ВНЗ / Р. М. Трохимчук. — К. : Вид. дім «Професіонал», 2010. — 528 c.
- Дискретна математика: навч. посіб. для студентів напрямів підгот. «Комп'ютерні науки» та «Економічна кібернетика» / Є. В. Гвоздьова, М. О. Гірник; Укоопспілка, Львів. комерц. акад. — Львів: Вид-во Львів. комерц. акад., 2015. — 123 c. — Бібліогр.: с. 123.
- Дискретна математика: підручник / Ю. В. Нікольський, В. В. Пасічник, Ю. М. Щербина ; за наук. ред. В. В. Пасічника ; М-во освіти і науки. молоді та спорту України. — 3-тє вид., виправл. та доповн. — Львів: Магнолія-2006, 2013. — 432 с. : іл. — (Серія «Комп'ютинг»). — Бібліогр.: с. 430—431 (52 назви). — ISBN 978-966-2025-76-7
- Дрозд Ю. А. Дискретна математикаPDF. — Київ : Київський Національний університет імені Тараса Шевченка, 2004. — 71 с.
- С. Л. Кривий. Курс дискретної математики : навчальний посібник. — Київ : Книжкове видавництво Національного авіаційного університету, 2007. — 430 с. — ISBN 9665983539.
- Основи дискретної математики: навч. посіб. Ч. 2. Математична логіка. Теорія графів / В. С. Ільків, П. І. Каленюк, І. В. Когут, З. М. Нитребич, П. Я. Пукач, П. Л. Сохан, Р. Р. Столярчук, У. Б. Ярка; МОНМС України, Нац. ун-т «Львів. політехніка». — Львів, 2011. — 184 c. — Бібліогр.: с. 177—179.
- Ямненко Р. Є. Дискретна математика: навчально-методичний посібник PDF. — Київ : Четверта хвиля, 2010. — 105 с. — ISBN 978-966-529-232-6.
- Дискретна математика (Електронний ресурс): розрахункові роботи для студентів спеціальностей 124 «Системний аналіз», 122 «Комп'ютерні науки» / КПІ ім. Ігоря Сікорського ; уклад. І. Я. Спекторський, О. В. Стусь, В. М. Статкевич. — Електронні текстові дані (1 файл: 578 Кбайт). — Київ: КПІ ім. Ігоря Сікорського, 2017. — 84 с. — Назва з екрана.
Іншими мовами[ред. | ред. код]
- Epp, Susanna S. (2010). Discrete Mathematics (вид. Fourth). Cengage Learning. с. 984. ISBN 978-0495391326. (англ.)
- Grimaldi, Ralph (1998). Discrete and Combinatorial Mathematics: An Applied Introduction (вид. Fourth). Addison Wesley Publishing Company. с. 896. ISBN 978-0201199123. (англ.)
- Rosen, Kenneth (2006). Discrete Mathematics and Its Applications (вид. 6th). McGraw-Hill Education. с. 1006. ISBN 978-0073229720. (англ.)
- Anderson, James A. (2000). Discrete Mathematics with Combinatorics (вид. First). Prentice Hall. с. 799. ISBN 978-0130869982. (англ.)
- Белоусов А. И., Ткачев С. Б. Дискретная математика. Серия: Математика в техническом университете. Изд-во: МГТУ им. Н. Э. Баумана, 2001.- 744 с. ISBN 5-7038-1769-2, ISBN 5-7038-1270-4 (рос.)
- Ерусалимский Я. М. Дискретная математика. — М., 2000. (рос.)
- Иванов Б. Н. Дискретная математика. Алгоритмы и программы. Издательство: Физматлит, 2007. — 408 с. ISBN 978-5-9221-0787-7 (рос.)
- Редькин Н. П. Дискретная математика. Издательство: Лань, 2006. — 96 с. ISBN 5-8114-0522-7 (рос.)
- Яблонский С. В. Введение в дискретную математику. — М. : Наука, 1979. — С. 272. (рос.)
Примітки[ред. | ред. код]
- ↑ Wilson, Robin (2002). Four Colors Suffice. London: Penguin Books. ISBN 0-691-11533-8.
- ↑ Символ (від грец. εστι — «бути») введений італійським математиком Джузеппе Пеано.
- ↑ S. E. Goodman, S. Hedentiemi (1977). Introduction to the Design and Analysis of Algorithms [Введення в розробку та аналіз алгоритмів] (англійська) . с. 47. Архів оригіналу за 28 лютого 2020. Процитовано 30 листопада 2020.
- ↑ Вентцель Е. С. Исследование операций: задачи, принципы, методология. — М. : Наука, Главная редакция физико-математической литературы, 1980. — ISBN 5-02-013900-9.
Посилання[ред. | ред. код]
- Юрій Дрозд. Дискретна математика.PDF — підручник до вступного курсу дискретної математики. (укр.)
- Карнаух Т. О., Ставровський А. Б. Вступ до дискретної математики Навчальний посібник [Архівовано 5 липня 2016 у Wayback Machine.]. (укр.)
- Дискретна Математика :: ВступPDF
- ДИСКРЕ́ТНИЙ АНА́ЛІЗ [Архівовано 22 квітня 2016 у Wayback Machine.] //ЕСУ
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Це незавершена стаття з математики. Ви можете допомогти проєкту, виправивши або дописавши її. |



















































