Показник заломлення
| Показник заломлення | ||||
| Символи: | ||||
|---|---|---|---|---|
| Одиниці вимірювання | ||||
| Розмірність: | безрозмірнісна | |||
|
| ||||

Показник заломлення — безрозмірнісна фізична величина, що характеризує відмінність фазових швидкостей світла в двох середовищах.
Для прозорих ізотропних середовищ, як-от гази, більшість рідин, аморфні речовини (наприклад, скло), вживають термін абсолютний показник заломлення (позначається латинською літерою ), який визначають як відношення швидкості світла у вакуумі до фазової швидкості світла в даному середовищі:
де — швидкість світла у вакуумі, — фазова швидкість світла в середовищі. Наприклад, показник заломлення води становить 1,333, що означає, що у воді світло рухається в 1,333 рази повільніше, ніж у вакуумі (приблизно 225 000 км/с).
У випадку двох довільних середовищ говорять про відносний показник заломлення одного середовища відносно іншого. Якщо не зазначено інше, то зазвичай йдеться про абсолютний показник заломлення.
Значення абсолютного показника заломлення залежить від складу та будови речовини, її агрегатного стану, температури, тиску тощо. Для деяких речовин показник заломлення змінюється під дією зовнішнього електричного поля (ефект Керра — в рідинах і газах; ефект Покельса — в кристалах).
Для вимірювання показника заломлення застосовують рефрактометри.
Для конкретної речовини фазова швидкість, а отже й показник заломлення, залежить від частоти світла — це явище має назву дисперсії. Показник можна обчислити й для електромагнітного випромінювання поза видимим діапазоном.
Абсолютний показник заломлення здебільшого перевищує одиницю, оскільки швидкість розповсюдження світла в будь-якому середовищі менша за швидкість світла у вакуумі. Однак фазова швидкість світла за деяких умов може перевищувати швидкість його розповсюдження, і тоді показник заломлення може набувати значень менших за одиницю.
Закони заломлення для прозорих середовищ можна формально узагальнити й на середовища з поглинанням, якщо показник заломлення розглядати як комплексну величину:
- , де — уявна одиниця, — показник поглинання.
Заломлення на межі двох середовищ[ред. | ред. код]

Коли світло проходить межу двох середовищ, то для обчислення кута заломлення використовують відносний показник заломлення, що дорівнює відношенню абсолютних показників заломлення першого і другого середовищ. Відносний показник заломлення може бути більшим за одиницю, якщо промінь переходить в середовище з більшою оптичною густиною і меншим у протилежному випадку[1].
Якщо промінь переходить з середовища з меншим показником заломлення в середовище з більшим (наприклад, з повітря у воду), то кут між променем і нормаллю до межі розділу зменшується після заломлення і навпаки, у випадку переходу в середовище з меншою оптичною густиною кут збільшується. У другому випадку кут заломлення може перевищувати 90° і в такому випадку заломлення не відбувається взагалі, тобто все світло відбивається; це явище називається повне внутрішнє відбиття[2].
Частота світла не змінюється при заломленні. Тому довжина хвилі світла у середовищі зменшується порівняно з довжиною хвилі у вакуумі пропорційно сповільненню світла[3].
Зв'язок між швидкістю та кутом заломлення світла[ред. | ред. код]

За принципом Ферма світло розповсюджується траєкторією, яка потребує найменше часу, щоб здолати шлях з однієї точки до іншої[4].
Якщо швидкість у двох середовищах становить і відповідно, то час руху з точки А в точку В залежить від вибору точки P на межі між середовищами:
У мінімумі функції її похідна набуває нульового значення:
Враховуючи, що
- ,
- ,
вираз спрощується до
- ,
із чого випливає, що
- або .
Останнє рівняння також відоме як закон Снеліуса[5].
Коефіцієнт відбиття[ред. | ред. код]

Під час падіння на межу поділу двох середовищ лише частина світла проходить з середовища з меншим показником заломлення у середовище з більшим, а частина — відбивається назад. Частина світла, що відбивається, є тим більшою, чим сильніше відрізняються показники заломлення середовищ. У випадку падіння світла по нормалі до поверхні коефіцієнт відбиття виражається як[6]:
- .
У такому випадку, під час переходу світла з повітря в скло (показник заломлення 1,33) відбивається 4 % падаючого світла, а у випадку діаманта (показник заломлення 2,42[7]) — понад 17 %.
Розрахувати відбиття світла для довільних кутів падіння й поляризації можна за допомогою формул Френеля.
Поляризація заломленого світла[ред. | ред. код]

Інтенсивності заломленої і відбитої хвилі залежать від поляризації падаючого світла — s-поляризоване світло більше відбивається, тоді як p-поляризоване проходить у середовище. Через це, навіть якщо на границю середовищ падає неполяризоване світло, і заломлений, і відбитий промені є частково поляризованими (якщо кут падіння не нульовий). У випадку, якщо кут між відбитим і заломленим променями становить 90°, відбите світло стає повністю поляризованим. Кут падіння, за якого це відбувається, називається кутом Брюстера. Його значення залежить від показника заломлення другого середовища відносно першого[8]:
- .
У випадку падіння під таким кутом заломлений промінь не стає повністю поляризованим, але ступінь його поляризації є максимальним[8].
Механізм сповільнення світла у середовищі[ред. | ред. код]
Причини сповільнення світла у речовині можуть бути (зі спрощеннями) пояснені з позицій класичної електродинаміки.
Будь-яка заряджена частинка в полі електромагнітної хвилі зазнає дії періодичних сил, що спричинюють її коливання. Зазвичай важливішою є дія періодичного електричного поля, а не магнітного, оскільки швидкості частинок в середовищі є відносно невисокими. Під дією періодичного електричного поля носії електричного заряду також починають коливатись з деякою частотою, а отже самі стають джерелами електромагнітних хвиль[9].
Атоми всіх речовин містять електрони — легкі заряджені частинки, які легко змусити коливатися. У випадку хвиль оптичного діапазону (частотою порядку 1015 Гц) поле, створюване електронами, зазвичай майже повністю описує наведене поле. Для хвиль меншої частоти (інфрачервоного або мікрохвильового випромінювання) помітними стають і ефекти, що спричинені перерозподілом електронів між атомами у молекулі, коливанням іонів у іонних кристалах або обертанням полярних молекул[10].
Хвилі, що створюються кожним електроном, інтерферують між собою, створюючи хвилю, що розповсюджується у тому ж напрямку, що і падаюча хвиля (а також у протилежному — що сприймається як відбиття від границі середовищ)[11].
Інтерференція падаючої хвилі з наведеною створює ефект сповільнення електромагнітної хвилі (хоча насправді, обидві хвилі рухаються з однаковою швидкістю — швидкістю світла)[12].
У загальному випадку обчислення поля, яке створюється коливанням електронів, є складною задачею, оскільки кожен електрон зазнає дії не тільки падаючої хвилі, але і хвилі, створеної коливаннями всіх інших електронів[11]. Найпростіша модель виводиться з припущення, що дія електронів один на одного є нульовою, що справедливо для дуже розріджених середовищ з низьким показником заломлення, таких як гази[11].
Нехай на тонкий шар речовини товщиною падає монохроматична плоска хвиля з циклічною частотою , що розповсюджується вздовж напрямку . Електричне поле у ній змінюється за законом:
- .
Інтенсивність звичайних (не лазерних) джерел світла порівняно невелика й напруженість електричного поля світлової хвилі значно менша від напруженості електричного поля в атомі. За таких умов електрон в атомі можна розглядати як гармонічний осцилятор[1] (це припустимо з позицій квантової механіки) з резонансною частотою (для більшості речовин ця частота лежить в ультрафіолетовому діапазоні). Рівняння руху електрона, що знаходиться на самому початку пластинки (у точці z=0) під дією зовнішньої періодичної сили буде описуватися звичайним для такої системи рівнянням[13]:
,
де і — маса і заряд електрона відповідно.
Розв'язок такого рівняння має вигляд[14]:
- .
Якщо джерело випромінювання знаходиться достатньо далеко і фронт падаючої хвилі плаский, всі електрони, що знаходяться у цій площині, рухаються однаково. Поле, що створюється такою площиною дорівнює[14]:
- ,
де — число заряджених частинок на одиницю площі.
З іншого боку, якщо у пластинці хвиля сповільнюється в разів, рівняння хвилі після проходження через пластинку буде мати вигляд[15]:
- .
Це рівняння описує хвилю, ідентичну падаючій, але з затримкою по фазі (яку виражає перша експонента).
У випадку малої товщини пластинки можна розкласти першу експоненту у ряд Тейлора[16]:
Таким чином, поле, що створюється речовиною, описується формулою:
- .
Порівнюючи цей вираз з виразом, отриманим для поля, створеного коливаннями електронів, можна отримати:
- .
Оскільки число зарядів на одиницю площі дорівнює концентрації електронів , помноженій на товщину пластинки, величина показника заломлення дорівнює[17]:
- ,
де — діелектрична проникність вакууму.
Ця формула також описує залежність показника заломлення від частоти падаючої хвилі — явище дисперсії[17].
Для правильного обчислення необхідно враховувати, що кожен атом містить багато електронів, що мають різні резонансні частоти. Їх внески мають сумуватися у правій частині рівняння[18].
В інтенсивних світлових потоках напруженість електричного поля хвилі може бути співвимірною з внутрішньоатомною. У таких умовах модель гармонічного осцилятора стає неприйнятною [1].
Нелінійна оптика[ред. | ред. код]
Показник заломлення змінюється в електричному полі — це явище відоме як ефект Керра (у рідинах і газах) або ефект Покельса (у кристалах). Оскільки сама електромагнітна хвиля також несе змінне електричне поле, показник заломлення залежить від інтенсивності світла. Залежність має вигляд , де - падаючої хвилі, — нелінійний індекс рефракції , який має значення 10−14 — 10−16 см2/Вт[19], тому ефект стає помітним лише за високої інтенсивності світла. Для потужних лазерів він виявляється в явищах самофокусування[en], генерації другої гармоніки тощо.
Дисперсія[ред. | ред. код]

Показник заломлення залежить від частоти світла. Ця залежність називається дисперсією.
У тих діапазонах, де речовина прозора, заломлення збільшується з частотою[20]. Наприклад, вода та безбарвне скло заломлюють блакитне світло сильніше, ніж червоне.
У природі цей ефект призводить до виникнення веселки. Розкладання світла скляною призмою заклало основи спектрального аналізу, що широко застосовується в науці й техніці.
Водночас дисперсія призводить до труднощів у виготовленні оптичних систем. Коли на скляну лінзу падає пучок немонохроматичного світла, то промені різних кольорів фокусуються на різній відстані й навколо контрастних деталей зображення утворюється райдужна облямівка. Явище отримало назву хроматичної аберації. Її компенсують шляхом виготовлення лінз із різних сортів оптичного скла, що мають різні показники заломлення[21].
Через залежність показника від довжини хвилі в таблицях зазначають для якої частоти його виміряно. Зазвичай застосовується частота жовтої лінії натрію (точніше, оскільки ця спектральна лінія є подвійною, застосовується середнє арифметичне від довжин ліній дублету, 5893 Å), у цьому випадку показник заломлення позначається через [22].
Для оцінки дисперсії в оптичному діапазоні застосовують середню дисперсію (), що дорівнює різниці показників заломлення для червоної (λC=6563 Å) та синьої ліній водню (λF=4861 Å)[22]. F і C — позначення відповідних фраугоферових ліній[23].
Іншим показником є число Аббе, що дорівнює[24]:
Більше число Аббе відповідає меншій середній дисперсії.

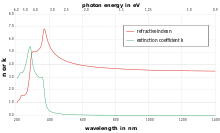
У широкому діапазоні електромагнітних хвиль залежність показника заломлення від частоти є нелінійною і складається з ділянок, де показник заломлення зростає з частотою — цей випадок називається нормальною дисперсією (оскільки така ситуація є типовою), — і невеликих ділянок, де показник заломлення стрімко падає, що називається аномальною дисперсією. Ділянки аномальної дисперсії зазвичай розташовані поблизу ліній поглинання речовини[25].
Показник заломлення менший за одиницю[ред. | ред. код]
Фазова швидкість світла в речовині може бути більшою за швидкість світла у вакуумі (це не суперечить СТО, оскільки енергія та інформація передається груповою швидкістю, яка не перевищує швидкості світла). У таких випадках показник заломлення може бути менший за одиницю. В оптичному діапазоні показник заломлення практично завжди більший за одиницю, проте в ультрафіолетовому, а особливо в рентгенівському діапазоні показники менші одиниці є типовими[26].
Висока фазова швидкість рентгенівського випромінювання в речовині зумовлена взаємодією випромінювання й електронних оболонок атомів — у м'якому рентгенівському діапазоні лежить багато ліній поглинання (K-серії). Показник заломлення для цього діапазону дуже близький до одиниці, і часто записується як , де — додатне й має значення порядку 10−4..10−6[27].
Такі показники заломлення призводять до особливих ефектів, наприклад, увігнуті лінзи для такого випромінювання працюють як опуклі і навпаки. Оскільки вакуум є оптично густішим середовищем, ніж речовина, то при падінні на речовину під малим кутом рентгенівське випромінювання може зазнавати повного внутрішнього відбиття[28]. Цей ефект застосовують у рентгенівських телескопах.
Показник заломлення для непрозорих середовищ[ред. | ред. код]
На відміну від ідеальних для реальних середовищ часто необхідно враховувати згасання сигналу при проходженні через них. Для цього застосовують комплексну величину[29]
- ,
де — уявна одиниця, — показник поглинання світла у речовині.
У цій формі можна записати хвильове рівняння у речовині (для хвилі, що рухається в напрямку і поляризована в напрямку x) як[30]
- .
Після підстановки комплексного показника заломлення в це рівняння, експонента розпадеться на дві, одна з яких має дійсне від'ємне значення показника. Таким чином, інтенсивність світла у речовині спадає за експоненційним законом.
Комплексні показники заломлення застосовуються:
- для опису взаємодії світла з непрозорими речовинами, такими як метали (у цьому випадку показник поглинання значний, більший за одиницю, і хвиля повністю поглинається за кілька мікрометрів)
- для опису проходження електромагнітної хвилі через середовище, якщо її частота є близькою до частоти поглинання атомів цього середовища (зони аномальної дисперсії)[31]
- для опису заломлення полярними рідинами (наприклад, водою), особливо у випадку низькочастотного випромінювання[32]
- в інших випадках, коли шар речовини достатньо товстий, щоб необхідно було враховувати поглинання.
Зв'язок із іншими показниками[ред. | ред. код]
Діелектрична проникність[ред. | ред. код]
З рівнянь Максвелла можна отримати формулу, що пов'язує швидкість світла в середовищі з його діелектричною й магнітною проникністю (позначаються літерами та відповідно)[33]
- .
Таким чином, показник заломлення визначається характеристиками середовища[34]:
- .
У більшості реальних прозорих речовин магнітна проникність дуже близька до одиниці, тому останню формулу іноді спрощують до .
Діелектрична проникність у цій формулі може значно відрізнятись від табличних значень, оскільки в таблицях зазвичай наведено значення проникності у постійному електричному полі. У полі, що швидко змінюється (саме таке поле створює електромагнітна хвиля), молекули не встигають поляризуватись, що призводить до зменшення діелектричної проникності. Особливо це стосується полярних молекул таких як вода: діелектрична проникність води в постійному електричному полі = 81, проте для полів, що змінюються з частотою 1014 — 1015 Гц (оптичний діапазон), вона падає до 1,78[35].
У випадку кристалів й інших анізотропних середовищ діелектрична проникність залежить від напрямку й описується тензором, тому показник заломлення є тензорною величиною[36].
Поляризовність[ред. | ред. код]
Важливим рівнянням, що пов'язує показник заломлення з мікроскопічними властивостями речовини, є рівняння Лоренца — Лоренца[37]:
- ,
де — електронна поляризовність молекул (залежить від частоти), а — їх концентрація.
У випадку, якщо заломлююче середовище є сумішшю кількох речовин, то у правій частині рівняння буде стояти кілька доданків, кожен з яких відповідає окремому компоненту.
Величину
- ,
де — молекулярна маса, іноді називають молекулярною рефракцією[38]. Вона майже не залежить від тиску, температури й навіть агрегатного стану і є характеристикою поляризовності молекул конкретної речовини.
У простішому випадку газу з невеликим тиском показник заломлення виражається як[29]
- .
Формула Лоренца — Лоренца виведена у припущенні ізотропності середовища, тому є справедливою для газів, рідин, аморфних тіл. Проте і для багатьох інших речовин вона часто виконується з хорошою точністю (похибка не перевищує кількох відсотків). Придатність формули для конкретної речовини визначається експериментально. Для деяких класів речовин, наприклад, пористих матеріалів, похибка може досягати десятків відсотків[39]. Область використання формули обмежується видимим і ультрафіолетовим діапазоном світла та виключає діапазони поглинання випромінювання у речовині[37]. Для нижчих частот необхідно враховувати не тільки електронну поляризацію, але й атомну (оскільки іони в іонних кристалах і атоми в молекулах встигають зміститися в полі низької частоти).
Для полярних діелектриків у випадку хвиль великої довжини також необхідно враховувати орієнтаційну поляризовність, природа якої полягає у зміні орієнтації дипольних молекул вздовж силових ліній поля. Для газів, що складаються з полярних молекул або сильно розведених розчинів полярних речовин у неполярних розчинниках, замість формули Лоренца — Лоренца необхідно використовувати формулу Ланжевена — Дебая[10]:
- ,
де — молекулярна маса, — густина, — стала Авогадро, — сума атомної й електронної поляризовності.
Густина[ред. | ред. код]
У цілому речовини з більшою густиною мають вищий показник заломлення. Для рідин показник заломлення зазвичай більший ніж у газів, а у твердих тіл — більший ніж у рідин[40]. Проте кількісний зв'язок може бути різним для різних класів речовин. Існує кілька емпіричних формул, що дозволяють оцінити цей зв'язок чисельно[41]. Найбільш відомим є рівняння, що виводиться з Формули Лоренца — Лоренца:
- .
Вона добре описує гази, а також задовільно виконується у випадку зміни агрегатного стану речовини[41].
Величину іноді називають як питомою рефракцією[42].
У випадку газів низького тиску цей вираз зводиться до ще простішого, відомого як закон Гладстона — Дела[43]:
- .
Зменшення густини повітря з висотою (відповідно, зменшення показника заломлення) спричиняє рефракцію світла в атмосфері, що призводить до зсуву видимого положення небесних світил. Поблизу горизонту такий зсув сягає 30 кутових мінут (тобто, розміру диску Сонця чи Місяця)[44].
Для деяких немагнітних середовищ точнішу оцінку можна отримати за допомогою формули, виведеної Макдональдом:
- .
Вона краще описує показник заломлення для води, бензену та інших рідин[41].

Також існує залежність показника заломлення від деяких інших, пов'язаних з густиною величин: він зменшується при збільшенні температури (через зменшення концентрації частинок внаслідок термічного розширення)[40]. Із тих самих причин при збільшенні тиску показник заломлення зростає[45].
Із рівняння Ланжевена — Дебая видно, що для полярних діелектриків ця залежність є складнішою, але якісно такою ж (при підвищенні температури показник заломлення падає, при підвищенні тиску — росте).
У нерівномірно нагрітому повітрі внаслідок змін показника заломлення траєкторія променів світла викривлюється й спостерігаються міражі.
Похідні величини[ред. | ред. код]
У нафтохімії застосовується похідний від густини показник — рефрактометрична різниця або інтерцепт рефракції:
- .
Ця величина однакова для вуглеводнів одного гомологічного ряду[46].
Особливі випадки[ред. | ред. код]
Від'ємний показник заломлення[ред. | ред. код]
У 1967 році В. Г. Веселаго висловив гіпотезу про існування матеріалів із від'ємним значенням показника заломлення — у таких матеріалах фазова і групова швидкості хвиль мають різний напрям[47].
В 1999 р. Джон Пендрі з Імперського коледжу в Лондоні запропонував конструкції штучних матеріалів, що мали від'ємні ефективні значення діелектричної й магнітної проникності[48].
В 2000 р. Девід Сміт (англ. David R. Smith) з колегами з Каліфорнійського університету в Сан-Дієго, застосував комбінацію елементів конструкцій Джона Пендрі і його рекомендації, щоб експериментально довести можливість реалізації штучних матеріалів із від'ємним значенням показника заломлення[49].
Такі метаматеріали можуть дозволити подолати дифракційну межу при створенні оптичних систем («суперлінз»), що дозволить підвищити роздільну здатність мікроскопів, створити мікросхеми наномасштабу, підвищити щільність запису на оптичні носії інформації[50].
Вимірювання[ред. | ред. код]
Показник заломлення вимірюють за допомогою рефрактометрів, а метод аналізу, що базується на такому вимірюванні, називається рефрактометрією. Існує кілька принципових схем вимірювання цього показника.
Найпоширенішим є вимірювання кута повного внутрішнього відбиття. Перевагами цього способу є мала кількість речовини, необхідна для дослідження, а також їх компактність — наприклад, у рефрактометрі Аббе рідина заливається в тонку щілину між гіпотенузними гранями двох прямокутних призм, що мають високий показник заломлення[51]. За схожим принципом працює рефрактометр Пульфриха, але у ньому навпаки, світло спрямовується паралельно межі поділу двох середовищ і вимірюється кут, на який воно відхилилося.
Для дрібних твердих часток використовують імерсійний метод — частки занурюють у ряд рідин із відомими показниками заломлення і спостерігають за інтерференційної картиною, що утворюється. Таким чином знаходиться пара рідин, одна з яких матиме менший показник заломлення ніж досліджувана речовина, а друга — більший[52].
Значення показника заломлення для деяких середовищ[ред. | ред. код]
| Середовище | |
|---|---|
| Вакуум | 1 (за визначенням)[53] |
| Гелій | 1,000034388[54] |
| Повітря | 1,00028821[55] |
| Вуглекислий газ | 1,0004408[56] |
| Дисилан | 1,0016574[57] |
| Аерогель[58] | 1,02 |
| Лід | 1,3098[59] |
| Вода | 1,3333[35] |
| Ацетон | 1,3592[60] |
| Етанол | 1,3617[61] |
| Тефлон | 1,38[62] |
| Кухонна сіль | 1,5442[63] |
| ПЕТ | 1,5693[64] |
| Скло[Прим. 1] | 1,4645 — 2,1[65][66] |
| Алмаз | 2,419[7] |
| Муассаніт | 2,65[67] |
Деякі напівпровідники, непрозорі у видимому світлі, пропускають інфрачервоне випромінювання. Показники заломлювання у цьому діапазоні є значними: 3,46[68] для арсеніду галію і 3,56 для кремнію[69].
Наразі найбільший показник заломлення у вузькому діапазоні має сконструйований у 2011 році метаматеріал. Для частот поблизу 0,3 ТГц його показник заломлення досягає 38,6[70].
Рекордний від'ємний показник заломлення (-700) досягнуто у радіодіапазоні[71].
Значення показника заломлення може значно відрізнятися для кристалів, тонких плівок і наночастинок однієї і тієї ж речовини[72].
Історія[ред. | ред. код]
Першим із європейців, хто вивчав заломлення, був Архімед. Досліджуючи заломлення на межі води з повітрям, він правильно описав кілька законів заломлення й зору (наприклад, те, що падаючий і заломлений промінь лежать в одній площині, а люди сприймають зображення так, ніби промені світла завжди розповсюджуються прямолінійно). Також він встановив, що кут заломлення завжди менший за кут падіння (коли промінь йде з повітря у воду)[73].
Через 100 років після Архімеда питання рефракції вивчав інший видатний античний вчений Птолемей. Він вимірював кути заломлення при переході світла між повітрям і водою, повітрям і склом, водою й склом[74], намагаючись знайти залежність між ними, проте вважав, що така залежність має вигляд квадратичної функції, тому виведене ним рівняння лише наближено описувало закони заломлення[73]. Втім, це було перше математичне рівняння для цього процесу. У формулі Птолемея був наявний аналог показника заломлення — число, що залежало від пари середовищ і визначало залежність кута падіння від кута заломлення. Птолемей пов'язував сильніше заломлення з різницею густини середовищ. Також він, аналізуючи видимий рух зір, зробив правильне припущення, що світло зазнає заломлення при переході в атмосферу з навколишнього простору, подібно до заломлення під час переходу з повітря у воду (а отже, що оптична густина повітря відрізняється від порожнечі), проте не зміг описати це явище кількісно[73].
Правильно сформулювати закон заломлення вперше зміг перський вчений Ібн Сахл[en] у 984 році[73]. На жаль, його роботи не були відомими в Європі, тому зараз цей закон відомий як закон Снеліуса на честь Вілеброрда Снеліуса, який відкрив його у 1621 році.
У 1658 році П'єр Ферма сформулював принцип найменшого часу, що дозволив пов'язати заломлення на межі середовищ зі швидкістю світла у них[75].
На початку XVIII століття показники заломлення багатьох речовин виміряли Ісаак Ньютон і Френсіс Хоксбі[76]. Ньютон також помітив зв'язок між густиною середовища й показником заломлення та зміг сформулювати емпіричне рівняння, що пов'язувало ці величини (відоме зараз як правило Ньютона — Лапласа), згідно з яким величина прямо пропорційна густині[77]. Також Ньютон у 1666 році описав явище дисперсії під час проходження світла через скляну призму[78].
Розвиваючи зроблені Ньютоном дослідження дисперсії, у 1802 Волластон, а пізніше, незалежно від нього, Фраунгофер у 1814 створили спектроскоп і спостерігали темні лінії у спектрі Сонця і зір[79].
Також Волластон створив перший рефрактометр. 1869 року Ернст Аббе вдосконалив його схему і створив модель рефрактометра (рефрактометр Аббе), яка є однією з найпопулярніших і донині[80].
Термін «показник заломлення» (англ. index of refraction) вперше використав Томас Юнг у 1807[81].
Ймовірно, близько 1840 року Фокс Талбот вперше спостерігав явище аномальної дисперсії, проте кількісно проаналізував його П'єр Леру[en] у 1862[82].
У період з 1869 до 1875 року данський фізик Людвіг Лоренц сформулював у кількох роботах теорію, що пов'язувала показник заломлення з мікроскопічними властивостями речовини — електронною поляризовністю. Такий же результат у 1878 році незалежно отримав голландський фізик Гендрік Лоренц, який не був знайомий з роботами Людвіга Лоренца, оскільки ті були написані данською. Виведене ними рівняння відоме як формула Лоренца — Лоренца[77].
Див. також[ред. | ред. код]
Примітки[ред. | ред. код]
- ↑ Показник заломлення скла лежить у широкому діапазоні, залежно від його складу й якості.
Джерела[ред. | ред. код]
- ↑ а б в Прохоров, 1994, Преломления показатель.
- ↑ Прохоров, 1994, Полное внутреннее отражение.
- ↑ Фейнман, Лейтон, 1967, с. 86.
- ↑ Кикоин, А. (1984). Принцип Ферма. Квант. № 1. с. 36—38. Архів оригіналу за 18 січня 2020. Процитовано 26 січня 2020.
- ↑ Прохоров, 1998, Снелля закон.
- ↑ Light at Interfaces. University of Delaware. 2010. Архів оригіналу за 14 травня 2021. Процитовано 1 квітня 2021.
- ↑ а б Optical constants of C (Carbon, diamond, graphite, graphene, carbon nanotubes). Refractive index database. Архів оригіналу за 28 квітня 2021. Процитовано 28 квітня 2021.
- ↑ а б Савельев, 1988, с. 432.
- ↑ Фейнман, Лейтон, 1967, с. 84.
- ↑ а б Прохоров, 1983, с. 344.
- ↑ а б в Фейнман, Лейтон, 1967, с. 85.
- ↑ Фейнман, Лейтон, 1967, с. 83.
- ↑ Фейнман, Лейтон, 1967, с. 89.
- ↑ а б Фейнман, Лейтон, 1967, с. 90.
- ↑ Фейнман, Лейтон, 1967, с. 87.
- ↑ Фейнман, Лейтон, 1967, с. 88.
- ↑ а б Фейнман, Лейтон, 1967, с. 91.
- ↑ Фейнман, Лейтон, 1967, с. 94.
- ↑ Dr. Rüdiger Paschotta (2008). Nonlinear Index. RP Photonics Encyclopedia. Архів оригіналу за 7 березня 2021. Процитовано 30 березня 2021.
- ↑ Кузнецов С.И. Нормальная и аномальная дисперсия. Колебания и волны. Геометрическая и волновая оптика (Электронный учебник). Архів оригіналу за 12 серпня 2020. Процитовано 2 квітня 2021.
{{cite book}}: Проігноровано|вебсайт=(довідка) - ↑ Вакуленко, 2008, c. 30 (Апохромат).
- ↑ а б Барковский, Горелик, Городенцева, 1963, с. 105.
- ↑ Index of Refraction of Liquids (Refractometry) (PDF). Universität Leipzig. Архів оригіналу (PDF) за 17 червня 2021. Процитовано 31 березня 2021.
- ↑ Dr. Rüdiger Paschotta. Chromatic Dispersion. RP Photonics Encyclopedia. Архів оригіналу за 29 червня 2015. Процитовано 2 квітня 2021.
- ↑ Прохоров, 1988, с. 211.
- ↑ Prof. David Attwood (2009). Reflection And Refraction (PDF). berkeley.edu. Архів оригіналу (PDF) за 26 січня 2020. Процитовано 26 січня 2020.
- ↑ X-ray refraction. x-ray-optics.de. Архів оригіналу за 26 січня 2020. Процитовано 26 січня 2020.
- ↑ Сторижко, В.Е.; Ильяшенко, М.В.; Молодкин, В.Б.; Гаевский, А.Ю.; Денисенко, В.Л.; Денисенко, О.И.; Вершинский, С.А. (2010). Способы фокусировки рентгеновского излучения (PDF). Успехи физики металлов. 11: 1—17. Архів оригіналу (PDF) за 30 квітня 2019. Процитовано 26 січня 2020.
- ↑ а б Прохоров, 1994, с. 107.
- ↑ Фейнман, Лейтон, 1977, с. 58.
- ↑ Фейнман, Лейтон, 1967, с. 96.
- ↑ Fatuzzo, E.; Mason, P.R. (1967). A calculation of the complex dielectric constant of a polar liquid by the librating molecule method. Proceedings of the Physical Society. 90 (3). doi:10.1088/0370-1328/90/3/318. Архів оригіналу за 14 травня 2021. Процитовано 1 квітня 2021.
- ↑ Сивухин, 1977, с. 358.
- ↑ Прохоров, 1994.
- ↑ а б Optical constants of H2O, D2O (Water, heavy water, ice). Refractive index database. Архів оригіналу за 28 квітня 2021. Процитовано 28 квітня 2021.
- ↑ Шен, 1980, с. 67.
- ↑ а б Прохоров, 1983, с. 352.
- ↑ Прохоров, 1992, с. 195.
- ↑ Schwarz, Daniel; Wormeester, Herbert; Poelsema, Bene (2011). Validity of Lorentz–Lorenz equation in porosimetry studies. Thin Solid Films. 519 (9): 2994—2997. doi:10.1016/j.tsf.2010.12.053.[недоступне посилання]
- ↑ а б Иоффе, 1983, с. 23.
- ↑ а б в Burnett, D. (1927). The Relation between Refractive Index and Density. Mathematical Proceedings of the Cambridge Philosophical Society. 23 (8): 907—911. doi:10.1017/S0305004100013773. Архів оригіналу за 14 травня 2021. Процитовано 19 березня 2021.
- ↑ Прохоров, 1998, с. 211.
- ↑ Куинн, 1985, с. 133.
- ↑ Рефракція світла в атмосфері. Український астрономічний портал. Архів оригіналу за 14 травня 2021. Процитовано 7 квітня 2021.
- ↑ Иоффе, 1983, с. 25.
- ↑ Проскуряков, Драбкин, 1981, с. 57.
- ↑ Веселаго В. Г. Электродинамика веществ с одновременно отрицательными значениями ε и μ // УФН. — 1967. — Т. 92. — С. 517.
- ↑ Слюсар, Вадим. Метаматериалы в антенной технике: история и основные принципы // Электроника: наука, технология, бизнес. — 2009. — № 7. — С. 70—79.
- ↑ John B. Pendry; David R. Smith. Reversing Light with Negative Refraction : [англ.] // Physics Today : magazine [1]. — 2004. — Vol. 57, № 6. — С. 37—43.
- ↑ Дж. Пендри, Д. Смит (2006). В поисках суперлинзы. Elementy.ru. Архів оригіналу за 14 травня 2021. Процитовано 19 березня 2021.
- ↑ Костіна Т.А. Рефрактометрія. Фармацевтична енциклопедія. Архів оригіналу за 14 травня 2021. Процитовано 1 квітня 2021.
- ↑ Вакуленко, 2008, с. 317—318 (Метод імерсійний).
- ↑ The Speed of Light and the Index of Refraction. Rensselaer Polytechnic Institute. Архів оригіналу за 10 квітня 2021. Процитовано 30 квітня 2021.
- ↑ Optical constants of He (Helium). Refractive index database. Архів оригіналу за 28 квітня 2021. Процитовано 28 квітня 2021.
Standard conditions. 0 °C, 760 torr (101.325 kPa)
- ↑ Optical constants of Air. Refractive index database. Архів оригіналу за 28 квітня 2021. Процитовано 28 квітня 2021.
Wavelength: 0.5893μm, Standard conditions. 0 °C, 760 torr (101.325 kPa).
- ↑ Optical constants of CO2 (Carbon dioxide). Refractive index database. Архів оригіналу за 28 квітня 2021. Процитовано 28 квітня 2021.
- ↑ Watson, H.E.; Ramaswamy, K.L. (1936). The Refractive Index Dispersion and Polarization of Gases. Proceedings of the Royal Society of London. 156 (887): 144—157. Архів оригіналу за 14 травня 2021. Процитовано 26 січня 2020.
- ↑ Bellunato, T.; Calvi, M.; Matteuzzi, C.; Musy, Marco; Perego, D.L.; Storaci, B. (2007). Refractive index dispersion law of silica aerogel. European Physical Journal C. 52 (3): 759—764. doi:10.1140/epjc/s10052-007-0431-3. Архів оригіналу за 10 березня 2020. Процитовано 26 січня 2020.
- ↑ Optical constants of H2O, D2O (Water, heavy water, ice). Refractive index database. Архів оригіналу за 28 квітня 2021. Процитовано 28 квітня 2021.
- ↑ Optical constants of C3H6O (Acetone). Refractive index database. Архів оригіналу за 28 квітня 2021. Процитовано 28 квітня 2021.
- ↑ Optical constants of C2H5OH (Ethanol). Refractive index database. Архів оригіналу за 28 квітня 2021. Процитовано 28 квітня 2021.
- ↑ Gauch, M.; Ließmann, M.; Ehlers, H.; Ristau, D. (2013). Optical properties of fluorocarbon thin films prepared by ion beam sputtering of PTFE. Optical Interference Coatings. 2013: 16—21. doi:10.1364/OIC.2013.ThA.2. Архів оригіналу за 28 квітня 2021. Процитовано 28 квітня 2021.
- ↑ Optical constants of NaCl (Sodium chloride). Refractive index database. Архів оригіналу за 28 квітня 2021. Процитовано 28 квітня 2021.
- ↑ Optical constants of (C10H8O4)n (Polyethylene terephthalate, PET). Refractive index database. Архів оригіналу за 28 квітня 2021. Процитовано 28 квітня 2021.
- ↑ Optical constants of OHARA - BBH (Barium borate, high-index). Refractive index database. Архів оригіналу за 28 квітня 2021. Процитовано 28 квітня 2021.
- ↑ Optical constants of OHARA - FSL (Fluorosilicate, low-index). Refractive index database. Архів оригіналу за 28 квітня 2021. Процитовано 28 квітня 2021.
- ↑ Brilliance & Refractive Index. Moissanite & Jewelry Education.
- ↑ Optical constants of GaAs (Gallium arsenide). Refractive index database. Архів оригіналу за 28 квітня 2021. Процитовано 28 квітня 2021.
- ↑ Optical constants of Si (Silicon). Refractive index database. Архів оригіналу за 28 квітня 2021. Процитовано 28 квітня 2021.
- ↑ Muhan, Choi; Seung, Hoon Lee; Yushin, Kim; Seung, Beom Kang; Jonghwa, Shin; Min, Hwan Kwak; Kwang-Young, Kang; Yong-Hee, Lee; Namkyoo, Park (2011). A terahertz metamaterial with unnaturally high refractive index. Nature. 470: 369—373. doi:10.1038/nature09776. Архів оригіналу за 9 березня 2021. Процитовано 19 березня 2021.
- ↑ Donhee Ham (2012). Reluctant electrons enable «extraordinarily strong» negative refraction. Harvard.edu. Архів оригіналу за 26 січня 2020. Процитовано 26 січня 2020.
- ↑ Optical constants of TiO2 (Titanium dioxide). Refractive index database. Архів оригіналу за 17 березня 2020. Процитовано 26 січня 2020.
- ↑ а б в г Waldemar H. Lehn and Siebren van der Werf (2005). Atmospheric refraction: a history (PDF). University of Manitoba. Архів оригіналу (PDF) за 6 травня 2021. Процитовано 19 березня 2021.
- ↑ Jean-Luc Godet. A short recall about the history of the concept of refractive index (PDF). Université d'Angers. Архів оригіналу (PDF) за 6 травня 2021. Процитовано 19 березня 2021.
- ↑ Fermat’s principle. Britannica. 1998. Архів оригіналу за 10 серпня 2020. Процитовано 1 квітня 2021.
- ↑ Hutton, 1815, с. 299.
- ↑ а б Kragh, Helge (2018). The Lorenz-Lorentz Formula: Origin and Early History. Substantia. 2 (2): 7—18. doi:10.13128/substantia-56. Архів оригіналу за 14 травня 2021. Процитовано 1 квітня 2021.
- ↑ A spectrum of colours: the dispersion of light. Institute of Physics. Архів оригіналу за 14 квітня 2021. Процитовано 1 квітня 2021.
- ↑ Bursey, Maurice M. (2017). A brief history of spectroscopy. AccessScience. doi:10.1036/1097-8542.BR0213171. Архів оригіналу за 5 березня 2021. Процитовано 2 квітня 2021.
- ↑ History of refractometer. refractometer.pl. Архів оригіналу за 19 квітня 2021. Процитовано 2 квітня 2021.
- ↑ Wolfe, 2020, ch. 32.
- ↑ Williams, S.R. (1908). A Study of Dispersion in Highly Absorbing Media by Means of Channeled Spectra. Physical Review. 27 (1): 27—32. doi:10.1103/PhysRevSeriesI.27.27. Архів оригіналу за 14 травня 2021. Процитовано 1 квітня 2021.
Література[ред. | ред. код]
- Романюк М. О., Крочук А. С., Пашук І. П. Оптика. — Л. : ЛНУ ім. Івана Франка, 2012. — 564 с.
- Сивухин Д. В. Электричество // Общий курс физики. — М. : «Наука», 1977. — Т. 3. — 704 с.
- Шен И. Р. Принципы нелинейной оптики. — М. : «Наука», 1980. — 558 с.
- Проскуряков В. А., Драбкин А. Е. Химия нефти и газа. — Ленинград : «Химия», 1981. — 359 с.
- Барковский В. Ф., Горелик С. М., Городенцева Т. Б. Практикум по физико-химическим методам анализа. — М. : «Высшая школа», 1963. — 349 с.
- Иоффе Б. В. Рефрактометрические методы химии. — Ленинград : ГХИ, 1983. — 399 с.
- Прохоров О. М. Физический энциклопедический словарь. — М. : «Советская энциклопедия», 1983. — 928 с.
- Прохоров О. М. Ааронова — Бома эффект — Длинные линии // Физическая энциклопедия. — М. : «Советская энциклопедия», 1988. — Т. 1. — 703 с.
- Прохоров О. М. Магнитоплазменный — Поинтинга теорема // Физическая энциклопедия. — М. : Научное издательство «Большая российская энциклопедия», 1992. — Т. 3. — 672 с. — ISBN 5-8527-0019-3.
- Прохоров О. М. Поинтинга — Робертсона эффект — Стриммеры // Физическая энциклопедия. — М. : Научное издательство «Большая российская энциклопедия», 1994. — Т. 4. — 704 с. — ISBN 5-8527-0087-8.
- Прохоров О. М. Стробоскопические приборы — Яркость // Физическая энциклопедия. — М. : Научное издательство «Большая российская энциклопедия», 1998. — Т. 5. — 691 с.
- Фейнман Р. Ф., Лейтон Р. Излучение, волны, кванты // Фейнмановские лекции по физике. — М. : Мир, 1967. — Т. 3. — 235 с.
- Фейнман Р. Ф., Лейтон Р. Физика сплошных сред // Фейнмановские лекции по физике. — М. : Мир, 1977. — Т. 7. — 286 с.
- Hutton C. A Philosophical and Mathematical Dictionary. — London, 1815. — Т. 2. — 628 с.
- Wolfe W. L. Rays, Waves and Photons. — Iop Publishing Ltd, 2020. — 350 с. — ISBN 978-0-7503-2612-4.
- Куинн Т. Температура. — М. : Мир, 1985. — 448 с.
- Вакуленко М. О., Вакуленко О. В. Тлумачний словник із фізики. — К. : Видавничо-поліграфічний центр "Київський університет", 2008. — 767 с.
- Савельев И. В. Электричество и магнетизм. Волны. Оптика. // Курс общей физики: Учеб. пособие. — М. : «Наука», 1988. — Т. 2. — 496 с.
|
| ||||||||||||||||
|
|
Ця стаття належить до добрих статей української Вікіпедії. |



































































