| Рівняння Максвелла |
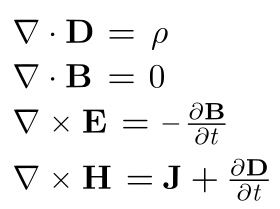 |
| Названо на честь |
Джеймс Клерк Максвелл |
|---|
| Дата публікації |
1861 |
|---|
| Формула |
 і і ![{\displaystyle {\begin{aligned}\partial _{[\alpha }F_{\beta \gamma ]}&=0,\\\partial _{\alpha }F^{\alpha \beta }&=\mu _{0}J^{\beta }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d0f82f0ab75cbffd5199c326253e1abe35d65d0) |
|---|
 |
| Підтримується Вікіпроєктом |
Вікіпедія:Проєкт:Математика |
|---|
| Є об'єднанням |
див. список:d |
|---|
 Рівняння Максвелла у Вікісховищі Рівняння Максвелла у Вікісховищі |
Рівня́ння Ма́ксвелла — це основні рівняння класичної електродинаміки, які описують електричне та магнітне поле, створене зарядами й струмами.
Рівняння електродинаміки в диференціальній формі[ред. | ред. код]
Форма запису рівнянь Максвелла залежить від системи одиниць. Здебільшого фізики користуються формою запису в системі СГСГ. У Міжнародній системі величин (ISQ), на базі якої побудована Міжнародна система одиниць (SI), вибрана форма запису, в якій не фігурують множник  та швидкість світла с. Ідея полягала в тому, щоб записати рівняння Максвелла як найфундаментальніші рівняння в найпростішій формі. Однак це призвело до появи зайвих множників в інших основних рівняннях, наприклад, законі Кулона. Крім того напруженості електричних та магнітного полів отримали різні розмірності, що з точки зору фізики є великим недоліком. Оскільки рівняння Максвелла описують розповсюдження електромагнітних хвиль, то бажано також, щоб їхня швидкість (швидкість світла) входила в рівняння.
та швидкість світла с. Ідея полягала в тому, щоб записати рівняння Максвелла як найфундаментальніші рівняння в найпростішій формі. Однак це призвело до появи зайвих множників в інших основних рівняннях, наприклад, законі Кулона. Крім того напруженості електричних та магнітного полів отримали різні розмірності, що з точки зору фізики є великим недоліком. Оскільки рівняння Максвелла описують розповсюдження електромагнітних хвиль, то бажано також, щоб їхня швидкість (швидкість світла) входила в рівняння.
У диференційній формі рівняння Максвелла для вакууму мають такий вигляд
 ,
,
 ,
,

 .
.
Рівняння записані в системі СГС. Тут  — напруженість електричного поля,
— напруженість електричного поля,  — вектор магнітної індукції,
— вектор магнітної індукції,
 — густина електричного заряду,
— густина електричного заряду,  — густина електричного струму,
— густина електричного струму,  — швидкість світла.
— швидкість світла.
У речовині електричне та магнітні поля характеризуються додатковими векторами: електричною індукцією та напруженістю магнітного поля, зв'язаних з, відповідно, напруженістю електричного поля й магнітною індукцією співвідношення, які називають матеріальними. У загальному вигляді матеріальні співвідношення мають складну нелокальну форму, тому при запису основних рівнянь електродинаміки їх не наводять. Рівняння набирають вигляду
 ,
,
 ,
,

 .
.
Тут  — густина вільних зарядів. Внесок зв'язаних зарядів враховується при визначенні вектора електричної індукці
— густина вільних зарядів. Внесок зв'язаних зарядів враховується при визначенні вектора електричної індукці  .
.
Міжнародна система величин[ред. | ред. код]
У Міжнародній системі величин (ISQ) навіть для вакууму вводяться дві додаткові характеристики електромагнітного поля: вектор електричної індукції та напруженість магнітного поля. У вакуумі вони пов'язані з напруженістю електричного поля та магнітною індукцією за допомогою сталих множників


 ,
,
де  — електрична стала,
— електрична стала,  — магнітна стала,
— магнітна стала,  — поляризація та намагніченість (сумарні дипольні моменти
— поляризація та намагніченість (сумарні дипольні моменти  ), тому система диференційних рівнянь Максвелла має такий вигляд:
), тому система диференційних рівнянь Максвелла має такий вигляд:
 ,
,
 ,
,
 .
.
У речовині рівняння зберігають свій вигляд, за винятком того, що матеріальні співвідношення, тобто зв'язкок між  та
та  ,
,  та
та  мають складнішу форму, і замість густини усіх електричних зарядів
мають складнішу форму, і замість густини усіх електричних зарядів  враховуються тільки вільні електричні заряди.
враховуються тільки вільні електричні заряди.
Перше рівняння Максвелла (закон Ампера) визначає магнітне поле, створене струмом із густиною  або ж наведене змінним електричним полем.
або ж наведене змінним електричним полем.
Друге рівняння Максвелла (закон Фарадея) визначає електричне поле, яке виникає при зміні напруженості магнітного поля.
Третє рівняння Максвелла (теорема Гауса) стверджує, що не існує монопольних магнітних зарядів.
Четверте рівняння Максвелла (рівняння Пуассона) стверджує, що навколо електричних зарядів існує електричне поле. Це рівняння аналогічне закону Кулона.
Згідно з легендою, приступаючи до роботи над створенням загальної теорії електромагнітних явищ, Джеймс Клерк Максвелл вирішив, що читатиме тільки експериментальні роботи. При виведенні своїх рівнянь він опирався на закон Кулона, який визначав силу взаємодії між зарядами, закон Ампера, що визначав силу взаємодії між струмами, закон електромагнітної індукції Фарадея, відсутність експериментальних даних, що вказували б на існування магнітного монополя та математичний апарат, розвинутий при вивченні явищ в області механіки й гідродинаміки.
Електричне та магнітні поля Максвелл уявляв собі, як механічні збурення певного середовища — ефіру. В 1820 році Ганс Крістіан Ерстед виявив[1], що проходячи через дріт гальванічний струм, змушує відхилятися магнітну стрілку компаса. Таке відкриття притягло широку уваги вчених того часу. В тому ж 1820 році Жан-Батіст Біо та Фелікс Савар експериментально знайшли вираз[2] для магнітної індукції, яка виникає (закон Біо — Савара — Лапласа), і Андре-Марі Ампер виявив, що взаємозв'язок на відстані з'являється також між двома дротами, через які проходить струм. Ампер увів термін «електродинамічний» і висунув гіпотезу, що природний магнетизм пов'язаний з існуванням в магніті кільцевих струмів[3].
Вплив струму на магніт, виявлений Ерстедом, призвело Майкла Фарадея до ідеї про те, що повинен існувати зворотний вплив магніту на струми. Після тривалих експериментів, в 1831 році, Фарадей відкрив, що магніт, який переміщається біля провідника, породжує в провіднику електричний струм. Це явище було названо електромагнітною індукцією. Фарадей ввів поняття «поля сил» — деякого середовища, що знаходиться між зарядами і струмами. Його міркування мали якісний характер, однак вони зробили величезний вплив на дослідження Максвелла.
Після відкриттів Фарадея стало ясно, що старі моделі електромагнетизму (Ампер, Пуассон та інші) неповні. Незабаром з'явилася теорія Вебера, заснована на далекодії. Проте відтоді вся фізика, крім теорії тяжіння, мала справу лише з близькодією (оптика, термодинаміка, механіка суцільних середовищ тощо). Гаус, Ріман і ряд інших вчених висловлювали припущення, що світло має електромагнітну природу, так що теорія електромагнітних явищ теж повинна бути близькодієвою. Цей принцип став суттєвою особливістю теорії Максвелла.
Максвелл вперше опублікував свої рівняння в 1861 році. В 1864 побачила світ інша його праця, в якій рівнянь було вісім, оскільки вони включали інші закони, які зараз не заведено включати в число рівнянь Максвелла. В 1884 Гевісайд за допомоги Гіббса вибрали першу систему 4-х рівнянь і переписали її у векторній формі, близькій до сучасної.
Рівняння Максвелла змінюють свій вигляд при переході від одної інерційної системи координат до іншої, якщо правила цього переходу задавати класичними перетвореннями Галілея. Ця обставина мало хвилювала Максвелла й інших вчених XIX сторіччя, оскільки вважалося, що рівняння справедливі лише в одній системі координат — тій, що зв'язана з непорушним ефіром.
У 1887 році Лармор знайшов перетворення, при яких рівняння Максвелла не змінюють вигляду при переході від одної неінерційної системи координат до іншої. Ці перетворення були названі перетвореннями Лоренца (Лоренц отримав їх у наближеному вигляді трошки раніше). Саме ці перетворення Ейнштейн поклав в основу спеціальної теорії відносності, яка відмовилася від ідеї про існування ефіру. Після цього рівняння Максвелла набули статусу універсального закону природи, справедливого в будь-якій системі координат. Проте їхня інтерпретація докорінно відрізняється від ідей, на основі яких Максвелл їх вивів.
Таблиця рівнянь у ISQ[ред. | ред. код]
У ISQ рівняння електродинаміки мають наступний вигляд:
| Lp. |
Диференціальне рівняння |
Інтегральне рівняння |
Назва |
Явище, котре описує рівняння
|
| 1.
|

|

|
закон Фарадея
|
Змінне у часі магнітне поле викликає вихрове електричне поле.
|
| 2.
|

|

|
Закон Ампера, розширений Максвеллом
|
Електричний струм і змінне електричне поле створюють магнітне поле.
|
| 3.
|

|

|
закон Гауса для електрики
|
Джерело електричного поля — заряди
|
| 4.
|

|

|
Закон Гауса для магнітного поля
|
Не існує заряду магнітного поля, силові лінії магнітного поля замкнені.
|
де:
 — оператор дивергенції [1/м],
— оператор дивергенції [1/м], — оператор ротора [1/м].
— оператор ротора [1/м].
Отримання рівнянь Максвелла у вакуумі із використанням СТВ, принципу суперпозиції та закону Кулона[ред. | ред. код]
Із отримання виразу для сили Лоренца, напруженістю електричного поля заряду, що рухається, є вираз
 ,
,
а індукцією магнітного поля —
![{\displaystyle \ \mathbf {B} ={\frac {1}{c}}[\mathbf {u} \times \mathbf {E} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b843a0d32d6506aeaf443e334a6bb9d996adfdba) .
.
Якщо у  підставити
підставити  , то значення відповідно напруженості та індукції буде нескінченно великим. Для уникнення цього можна штучно ввести константу
, то значення відповідно напруженості та індукції буде нескінченно великим. Для уникнення цього можна штучно ввести константу  як доданок у знаменник
як доданок у знаменник  (регуляризація). Тоді модифікований вираз набуде вигляду
(регуляризація). Тоді модифікований вираз набуде вигляду
 .
.
Для того, щоб показати, у якій мірі точки простору є джерелами та стоками електричного та магнітного полів, треба взяти дивергенцію від напруженості електричного поля та від індукції магнітного поля. З урахуванням попередніх перетворень,
Попередні перетворення.
 .
.
 .
.
 .
.
 .
.
,
з виразу  можна отримати:
можна отримати:
 ,
,
виведення.

 .
.
,
де

- тривимірна дельта-функція Дірака, яка дозволяє записати просторову густину заряду, зосередженого в одній точці. З неї видно, що  у кожній точці, крім як при
у кожній точці, крім як при  , у якій
, у якій  . Звідси можна стверджувати, базуючись на визначенні дивергенції, що електричний заряд — точка (у даному випадку), яка є джерелом електричної індукції.
. Звідси можна стверджувати, базуючись на визначенні дивергенції, що електричний заряд — точка (у даному випадку), яка є джерелом електричної індукції.
Перейшовши до неперервного розподілення зарядів у об'ємі та використавши аксіому принципа суперпозиції полів, суму тривимірних дельта-функцій Дірака можна замінити об'ємною густиною:
 .
.
Рівняння  є першим рівнянням Максвелла. Із нього можна отримати багато фізичних наслідків. Один з цих наслідків полягає у тому, що силові лінії поля починаються на додатному заряді і можуть замикатися лише на від'ємному, оскільки для додатного заряду
є першим рівнянням Максвелла. Із нього можна отримати багато фізичних наслідків. Один з цих наслідків полягає у тому, що силові лінії поля починаються на додатному заряді і можуть замикатися лише на від'ємному, оскільки для додатного заряду  відповідає витоку поля, а для від'ємного — його стоку.
відповідає витоку поля, а для від'ємного — його стоку.
Аналогічно можна отримати величину дивергенції магнітної індукції.
Для цього треба урахувати наступні попередні виведення.
Попередні перетворення.
![{\displaystyle [\nabla \times \varphi \mathbf {a} ]=\varphi [\nabla \times \mathbf {a} ]+[\mathbf {a} \times grad(\varphi )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba451817731c76b734e5b44bd207ae3732ecc239) .
.
![{\displaystyle [\nabla \times \mathbf {r} ]={\begin{vmatrix}\mathbf {\mathbf {i} } &\mathbf {\mathbf {j} } &\mathbf {\mathbf {k} } \\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\r_{x}&r_{y}&r_{z}\end{vmatrix}}={\frac {\partial z}{\partial y}}\mathbf {i} +{\frac {\partial x}{\partial z}}\mathbf {j} +{\frac {\partial y}{\partial x}}\mathbf {k} -{\frac {\partial x}{\partial y}}\mathbf {k} -{\frac {\partial y}{\partial z}}\mathbf {j} -{\frac {\partial z}{\partial x}}\mathbf {i} =0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e3b437d191d32fa9dc574af1608177c6284c32a) .
.
Тоді, користуючись тим, що, одразу,  , можна отримати, що
, можна отримати, що
 .
.
Виведення.
![{\displaystyle \ \nabla \mathbf {B} =(\nabla \cdot {\frac {1}{c}}[\mathbf {u} \times \mathbf {E} ])=-{\frac {1}{c}}(\mathbf {u} \cdot [\nabla \times \mathbf {E} ])=-{\frac {1}{c}}\left(\mathbf {u} \cdot [\nabla \times \mathbf {r} ]{\frac {Q\gamma }{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {3}{2}}}}\right)-{\frac {1}{c}}\left(\mathbf {u} \cdot \left[\mathbf {r} \times grad\left({\frac {kQ\gamma }{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {3}{2}}}}\right)\right]\right)=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c72cb6dabb4ea94345e109086ed3aaf83640d9ac)
![{\displaystyle \ =|[\nabla \times \mathbf {r} ]=0|={\frac {1}{c}}\left(\mathbf {u} \cdot \left[\mathbf {r} \times {\frac {3}{2}}{\frac {Q\gamma }{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {5}{2}}}}\left({\frac {\mathbf {r} }{r}}2r+2\gamma ^{2}\mathbf {u} {\frac {(\mathbf {r} \cdot \mathbf {u} )}{c^{2}}}\right)\right]\right)=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fedc773b1e648fc9d6fd2159639fbdecdac6ce4)
![{\displaystyle \ ={\frac {1}{c}}\left(\mathbf {u} \cdot \left[\mathbf {r} \times {\frac {3\mathbf {r} Q\gamma }{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {5}{2}}}}\right]\right)+{\frac {1}{c}}\left(\mathbf {u} \cdot \left[\mathbf {r} \times {\frac {3\mathbf {u} (\mathbf {r} \cdot \mathbf {u} )Q\gamma ^{3}}{c^{2}(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {5}{2}}}}\right]\right)={\frac {1}{c}}\left(\mathbf {u} \cdot {\frac {3[\mathbf {r} \times \mathbf {u} ](\mathbf {r} \cdot \mathbf {u} )Q\gamma ^{3}}{c^{2}(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {5}{2}}}}\right)=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e75888c102e9d563ddc24a765c70f5d950ff3ce)
![{\displaystyle \ =-{\frac {1}{c}}(\mathbf {r} \cdot [\mathbf {u} \times \mathbf {u} ]){\frac {3(\mathbf {r} \cdot \mathbf {u} )Q\gamma ^{3}}{c^{2}(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {5}{2}}}}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d8abb0d5432cfd9e854442f46127abe76078f49) .
.
Звідси очевидно, виходячи з поняття дивергенції, що жодна з точок простору у полі заряду, що рухається, включаючи точку положення самого заряду, не є джерелом магнітного поля.
Рівняння  є другим рівнянням Максвелла.
є другим рівнянням Максвелла.
Тепер, для визначеності закрученості поля в точках, можна взяти ротор від  .
.
З урахуванням же того, що швидкість руху ІСВ постійна, можна записати явний вираз для ротора магнітного поля:
![{\displaystyle \ [\nabla \times \mathbf {B} ]=[\nabla \times {\frac {1}{c}}[\mathbf {u} \times \mathbf {E} ]]={\frac {1}{c}}\mathbf {u} (\mathbf {E} \cdot \nabla )-{\frac {1}{c}}\mathbf {E} (\mathbf {u} \cdot \nabla )\qquad (.5)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad6b543d79f436643adf126cc057f98ac9453a52) .
.
Доведення.
![{\displaystyle \ [\nabla \times \mathbf {B} ]={\frac {1}{c}}{\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial x}}\\u_{y}E_{z}-u_{z}B_{y}&u_{z}E_{x}-u_{x}B_{z}&u_{x}E_{y}-u_{y}E_{x}\end{vmatrix}}={\frac {1}{c}}[u_{x}(E'_{y}+E'_{z})\mathbf {i} +u_{y}(E'_{x}+E'_{z})\mathbf {j} +u_{z}(E'_{x}+E'_{y})\mathbf {k} ]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8633034ac1217e12c9eb2395f53e0bce41b6929f)
![{\displaystyle \ ={\frac {1}{c}}[u_{x}(E'_{y}+E'_{y}+E'_{z})\mathbf {i} +u_{y}(E'_{y}+E'_{y}+E'_{z})\mathbf {j} +u_{z}(E'_{y}+E'_{y}+E'_{z})\mathbf {k} ]-{\frac {1}{c}}[E'_{x}u_{x}\mathbf {i} +E'_{y}u_{y}\mathbf {j} +E'_{z}u_{z}\mathbf {k} ]={\frac {1}{c}}\mathbf {u} (\mathbf {E} \cdot \nabla )-{\frac {1}{c}}\mathbf {E} (\mathbf {u} \cdot \nabla )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee8d4e0fe174f6f4812b8935eb25e49fd2b36021) .
.
Цей вираз можна видозмінити за допомогою наступних міркувань.
При аналізі руху ІСВ відносно заряду треба виразити радіус-вектор  у явному вигляді:
у явному вигляді:
 .
.
Тоді частинна похідна по часу напруженості електричного поля буде рівна
 .
.
Підставивши  у
у  , можна отримати:
, можна отримати:
![{\displaystyle \ [\nabla \times \mathbf {B} ]={\frac {1}{c}}\mathbf {u} (\mathbf {E} \cdot \nabla )-{\frac {1}{c}}\mathbf {E} (\mathbf {u} \cdot \nabla )={\frac {1}{c}}4\pi Q\delta _{a}(\mathbf {r} )\mathbf {u} +{\frac {1}{c}}{\frac {\partial \mathbf {E} }{\partial t}}={\frac {1}{c}}4\pi \mathbf {j} +{\frac {1}{c}}{\frac {\partial \mathbf {E} }{\partial t}}\qquad (.7)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc9943e1d897fc3431343d9d3ad662eba5f9bf81) ,
,
де  — густина струму.
— густина струму.
Рівняння  є третім рівнянням Максвелла. З нього видно, що при електричний струм або зміна його у часі породжують вихрове магнітне поле.
є третім рівнянням Максвелла. З нього видно, що при електричний струм або зміна його у часі породжують вихрове магнітне поле.
Ротор же від напруженості електричного поля буде рівен
![{\displaystyle \ [\nabla \times \mathbf {E} ]=[\nabla \times {\frac {Q\gamma \mathbf {r} }{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {3}{2}}}}]=[\nabla \times \mathbf {r} ]{\frac {Q\gamma }{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {3}{2}}}}-3Q\gamma {\frac {\left[\left(\mathbf {r} +{\frac {\gamma ^{2}}{c^{2}}}\mathbf {u} (\mathbf {u} \cdot \mathbf {r} )\right)\times \mathbf {r} \right]}{\left(r^{2}+{\frac {\gamma ^{2}}{c^{2}}}(\mathbf {u} \cdot \mathbf {r} )^{2}\right)^{\frac {5}{2}}}}=-{\frac {3[\mathbf {u} \times \mathbf {r} ](\mathbf {r} \cdot \mathbf {u} )Q\gamma ^{3}}{c^{2}(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {5}{2}}}}\qquad (.8)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0349c7d7b58306260315f9bb2078cf41b938c053) .
.
Вираз  , аналогічно до
, аналогічно до  , можна перетворити. Тоді
, можна перетворити. Тоді
![{\displaystyle \ [\nabla \times \mathbf {E} ]=-{\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}\qquad (.9)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a487cc74dd532eabff7bf0a6c164a43abad1ee34) .
.
Доведення.
Аналогічно до похідної по часу напруженості  , можна обчислити похідну від індукції магнітного поля
, можна обчислити похідну від індукції магнітного поля  :
:
![{\displaystyle \ {\frac {\partial \mathbf {B} }{\partial t}}=\sum _{i=1}^{3}{\frac {\partial \mathbf {B} }{\partial (r_{0_{i}}-u_{i}t)}}{\frac {\partial (r_{0_{i}}-u_{i}t)}{\partial t}}=-(\mathbf {u} \nabla )\mathbf {B} =-{\frac {Q\gamma }{c}}(\mathbf {u} \nabla )\left({\frac {[\mathbf {u} \times \mathbf {r} ]}{\left(r^{2}+{\frac {\gamma ^{2}}{c^{2}}}(\mathbf {u} \cdot \mathbf {r} )^{2}\right)^{\frac {3}{2}}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e53401af1933906052f69357ef533c26948e0af) .
.
Оскільки ![{\displaystyle \ (\mathbf {u} \nabla )[\mathbf {u} \times \mathbf {r} ]=[\mathbf {u} \times (\mathbf {u} \nabla )\mathbf {r} ]=[\mathbf {u} \times \mathbf {u} ]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4271c4bf065d772336299b2e61a2140c43528b9) , то векторний добуток можна винести за знак оператора похідної. Тоді
, то векторний добуток можна винести за знак оператора похідної. Тоді
![{\displaystyle \ =-{\frac {1}{c}}[\mathbf {u} \times \mathbf {r} ]{\frac {Q\gamma (\mathbf {u} \nabla )}{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {3}{2}}}}=-{\frac {1}{c}}{\frac {3Q\gamma (1+\gamma ^{2}u^{2})[\mathbf {u} \times \mathbf {r} ](\mathbf {u} \cdot \mathbf {r} )}{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {5}{2}}}}=-{\frac {1}{c}}{\frac {3Q\gamma ^{3}[\mathbf {u} \times \mathbf {r} ](\mathbf {u} \cdot \mathbf {r} )}{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {5}{2}}}}=-c[\nabla \times \mathbf {E} ]\Rightarrow }](https://wikimedia.org/api/rest_v1/media/math/render/svg/236f9c39110afdd3064f5a52bbd471d8e5af7811)
![{\displaystyle \ \Rightarrow [\nabla \times \mathbf {E} ]=-{\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b636a33b8731766b512b004e9d23e5353a1b36ba) .
.
Рівняння  є четвертим рівнянням Максвелла. З нього видно, що ротор напруженості електричного поля змінюється тільки тоді, коли є нестаціонарне магнітне поле (і, відповідно, напруженість електричного поля не сферично-симетрична через релятивістські ефекти — є виділений напрям руху заряду). У випадку із зарядом, який покоїться, поле сферично-симетричне, тому для нього ротор рівен нулю.
є четвертим рівнянням Максвелла. З нього видно, що ротор напруженості електричного поля змінюється тільки тоді, коли є нестаціонарне магнітне поле (і, відповідно, напруженість електричного поля не сферично-симетрична через релятивістські ефекти — є виділений напрям руху заряду). У випадку із зарядом, який покоїться, поле сферично-симетричне, тому для нього ротор рівен нулю.
На остачу залишилось написати про дві аксіоми, кожна з яких має досить вагомий внесок у можливість застосування отриманих рівнянь для електродинаміки.
Перша аксіома полягає у постулюванні векторної природи електромагнітного поля. Якщо б природа електромагнітного поля була тензорною, то для його описання знадобилися б рівняння на кшталт рівнянь ЗТВ. Наприклад, якщо формально застосувати ту ж методику, що продемонстрована у цьому розділі, до закону Всесвітнього тяжіння, то можна отримати рівняння, схожі до рівнянь Максвелла, як і вираз для сили, подібний до виразу сили Лоренца. Проте їх вірність не підтверджується експериментально, хоч якісно вони і вірно описують динаміку тіл у гравітаційному полі за умови справедливості принципу суперпозиції.
Друга ж аксіома пов'язана з постулюванням незалежності рівнянь Максвелла від прискорення заряду, що створює поле. Тобто, вони справедливі для будь-яких можливих випадків руху заряду.
Окрім цього, варто написати про принцип суперпозиції. Він може бути застосований до тих пір, поки поля, що створюються зарядами, не стануть настільки сильними, що будуть впливати на простір-час, унеможливлюючи представлення векторів-характеристик поля системи через лінійну комбінацію векторів зарядів цієї системи.
Незалежність рівнянь Максвелла[ред. | ред. код]
Користуючись рівнянням неперервності, можна перевірити систему рівнянь Максвелла на невиродженість. Взявши дивергенцію від роторного рівняння для індукції магнітного поля без підстановки  і виразивши з рівняння неперервності
і виразивши з рівняння неперервності  , можна отримати:
, можна отримати:
 .
.
Аналогічно можна взяти дивергенцію від четвертого рівняння Максвелла:
![{\displaystyle \ (\nabla \cdot [\nabla \times \mathbf {E} ])={\frac {\partial \nabla \mathbf {B} }{\partial t}}=0\Rightarrow \nabla \mathbf {B} =g(x,y,z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7833938bc25dbebf2e4181d524659b253e4543a4) .
.
Таким чином, із другої пари рівнянь Максвелла можна отримати першу тільки з точністю до функцій від координат, які не залежать від часу. Строго довести же, користуючись лише цими двома рівняннями, що функції рівні нулю, неможливо. Тому у цьому сенсі рівняння Максвелла (усього їх вісім — дві пари по три рівняння (оскільки роторні рівняння розпадаються на три компонентних рівняння)) є незалежними.
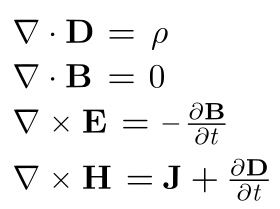

![{\displaystyle {\begin{aligned}\partial _{[\alpha }F_{\beta \gamma ]}&=0,\\\partial _{\alpha }F^{\alpha \beta }&=\mu _{0}J^{\beta }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d0f82f0ab75cbffd5199c326253e1abe35d65d0)





































![{\displaystyle \ \mathbf {B} ={\frac {1}{c}}[\mathbf {u} \times \mathbf {E} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b843a0d32d6506aeaf443e334a6bb9d996adfdba)



















![{\displaystyle [\nabla \times \varphi \mathbf {a} ]=\varphi [\nabla \times \mathbf {a} ]+[\mathbf {a} \times grad(\varphi )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba451817731c76b734e5b44bd207ae3732ecc239)
![{\displaystyle [\nabla \times \mathbf {r} ]={\begin{vmatrix}\mathbf {\mathbf {i} } &\mathbf {\mathbf {j} } &\mathbf {\mathbf {k} } \\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\r_{x}&r_{y}&r_{z}\end{vmatrix}}={\frac {\partial z}{\partial y}}\mathbf {i} +{\frac {\partial x}{\partial z}}\mathbf {j} +{\frac {\partial y}{\partial x}}\mathbf {k} -{\frac {\partial x}{\partial y}}\mathbf {k} -{\frac {\partial y}{\partial z}}\mathbf {j} -{\frac {\partial z}{\partial x}}\mathbf {i} =0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e3b437d191d32fa9dc574af1608177c6284c32a)


![{\displaystyle \ \nabla \mathbf {B} =(\nabla \cdot {\frac {1}{c}}[\mathbf {u} \times \mathbf {E} ])=-{\frac {1}{c}}(\mathbf {u} \cdot [\nabla \times \mathbf {E} ])=-{\frac {1}{c}}\left(\mathbf {u} \cdot [\nabla \times \mathbf {r} ]{\frac {Q\gamma }{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {3}{2}}}}\right)-{\frac {1}{c}}\left(\mathbf {u} \cdot \left[\mathbf {r} \times grad\left({\frac {kQ\gamma }{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {3}{2}}}}\right)\right]\right)=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c72cb6dabb4ea94345e109086ed3aaf83640d9ac)
![{\displaystyle \ =|[\nabla \times \mathbf {r} ]=0|={\frac {1}{c}}\left(\mathbf {u} \cdot \left[\mathbf {r} \times {\frac {3}{2}}{\frac {Q\gamma }{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {5}{2}}}}\left({\frac {\mathbf {r} }{r}}2r+2\gamma ^{2}\mathbf {u} {\frac {(\mathbf {r} \cdot \mathbf {u} )}{c^{2}}}\right)\right]\right)=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fedc773b1e648fc9d6fd2159639fbdecdac6ce4)
![{\displaystyle \ ={\frac {1}{c}}\left(\mathbf {u} \cdot \left[\mathbf {r} \times {\frac {3\mathbf {r} Q\gamma }{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {5}{2}}}}\right]\right)+{\frac {1}{c}}\left(\mathbf {u} \cdot \left[\mathbf {r} \times {\frac {3\mathbf {u} (\mathbf {r} \cdot \mathbf {u} )Q\gamma ^{3}}{c^{2}(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {5}{2}}}}\right]\right)={\frac {1}{c}}\left(\mathbf {u} \cdot {\frac {3[\mathbf {r} \times \mathbf {u} ](\mathbf {r} \cdot \mathbf {u} )Q\gamma ^{3}}{c^{2}(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {5}{2}}}}\right)=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e75888c102e9d563ddc24a765c70f5d950ff3ce)
![{\displaystyle \ =-{\frac {1}{c}}(\mathbf {r} \cdot [\mathbf {u} \times \mathbf {u} ]){\frac {3(\mathbf {r} \cdot \mathbf {u} )Q\gamma ^{3}}{c^{2}(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {5}{2}}}}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d8abb0d5432cfd9e854442f46127abe76078f49)


![{\displaystyle \ [\nabla \times \mathbf {B} ]=[\nabla \times {\frac {1}{c}}[\mathbf {u} \times \mathbf {E} ]]={\frac {1}{c}}\mathbf {u} (\mathbf {E} \cdot \nabla )-{\frac {1}{c}}\mathbf {E} (\mathbf {u} \cdot \nabla )\qquad (.5)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad6b543d79f436643adf126cc057f98ac9453a52)
![{\displaystyle \ [\nabla \times \mathbf {B} ]={\frac {1}{c}}{\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial x}}\\u_{y}E_{z}-u_{z}B_{y}&u_{z}E_{x}-u_{x}B_{z}&u_{x}E_{y}-u_{y}E_{x}\end{vmatrix}}={\frac {1}{c}}[u_{x}(E'_{y}+E'_{z})\mathbf {i} +u_{y}(E'_{x}+E'_{z})\mathbf {j} +u_{z}(E'_{x}+E'_{y})\mathbf {k} ]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8633034ac1217e12c9eb2395f53e0bce41b6929f)
![{\displaystyle \ ={\frac {1}{c}}[u_{x}(E'_{y}+E'_{y}+E'_{z})\mathbf {i} +u_{y}(E'_{y}+E'_{y}+E'_{z})\mathbf {j} +u_{z}(E'_{y}+E'_{y}+E'_{z})\mathbf {k} ]-{\frac {1}{c}}[E'_{x}u_{x}\mathbf {i} +E'_{y}u_{y}\mathbf {j} +E'_{z}u_{z}\mathbf {k} ]={\frac {1}{c}}\mathbf {u} (\mathbf {E} \cdot \nabla )-{\frac {1}{c}}\mathbf {E} (\mathbf {u} \cdot \nabla )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee8d4e0fe174f6f4812b8935eb25e49fd2b36021)





![{\displaystyle \ [\nabla \times \mathbf {B} ]={\frac {1}{c}}\mathbf {u} (\mathbf {E} \cdot \nabla )-{\frac {1}{c}}\mathbf {E} (\mathbf {u} \cdot \nabla )={\frac {1}{c}}4\pi Q\delta _{a}(\mathbf {r} )\mathbf {u} +{\frac {1}{c}}{\frac {\partial \mathbf {E} }{\partial t}}={\frac {1}{c}}4\pi \mathbf {j} +{\frac {1}{c}}{\frac {\partial \mathbf {E} }{\partial t}}\qquad (.7)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc9943e1d897fc3431343d9d3ad662eba5f9bf81)


![{\displaystyle \ [\nabla \times \mathbf {E} ]=[\nabla \times {\frac {Q\gamma \mathbf {r} }{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {3}{2}}}}]=[\nabla \times \mathbf {r} ]{\frac {Q\gamma }{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {3}{2}}}}-3Q\gamma {\frac {\left[\left(\mathbf {r} +{\frac {\gamma ^{2}}{c^{2}}}\mathbf {u} (\mathbf {u} \cdot \mathbf {r} )\right)\times \mathbf {r} \right]}{\left(r^{2}+{\frac {\gamma ^{2}}{c^{2}}}(\mathbf {u} \cdot \mathbf {r} )^{2}\right)^{\frac {5}{2}}}}=-{\frac {3[\mathbf {u} \times \mathbf {r} ](\mathbf {r} \cdot \mathbf {u} )Q\gamma ^{3}}{c^{2}(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {5}{2}}}}\qquad (.8)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0349c7d7b58306260315f9bb2078cf41b938c053)


![{\displaystyle \ [\nabla \times \mathbf {E} ]=-{\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}\qquad (.9)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a487cc74dd532eabff7bf0a6c164a43abad1ee34)


![{\displaystyle \ {\frac {\partial \mathbf {B} }{\partial t}}=\sum _{i=1}^{3}{\frac {\partial \mathbf {B} }{\partial (r_{0_{i}}-u_{i}t)}}{\frac {\partial (r_{0_{i}}-u_{i}t)}{\partial t}}=-(\mathbf {u} \nabla )\mathbf {B} =-{\frac {Q\gamma }{c}}(\mathbf {u} \nabla )\left({\frac {[\mathbf {u} \times \mathbf {r} ]}{\left(r^{2}+{\frac {\gamma ^{2}}{c^{2}}}(\mathbf {u} \cdot \mathbf {r} )^{2}\right)^{\frac {3}{2}}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e53401af1933906052f69357ef533c26948e0af)
![{\displaystyle \ (\mathbf {u} \nabla )[\mathbf {u} \times \mathbf {r} ]=[\mathbf {u} \times (\mathbf {u} \nabla )\mathbf {r} ]=[\mathbf {u} \times \mathbf {u} ]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4271c4bf065d772336299b2e61a2140c43528b9)
![{\displaystyle \ =-{\frac {1}{c}}[\mathbf {u} \times \mathbf {r} ]{\frac {Q\gamma (\mathbf {u} \nabla )}{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {3}{2}}}}=-{\frac {1}{c}}{\frac {3Q\gamma (1+\gamma ^{2}u^{2})[\mathbf {u} \times \mathbf {r} ](\mathbf {u} \cdot \mathbf {r} )}{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {5}{2}}}}=-{\frac {1}{c}}{\frac {3Q\gamma ^{3}[\mathbf {u} \times \mathbf {r} ](\mathbf {u} \cdot \mathbf {r} )}{(r^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}+a^{2})^{\frac {5}{2}}}}=-c[\nabla \times \mathbf {E} ]\Rightarrow }](https://wikimedia.org/api/rest_v1/media/math/render/svg/236f9c39110afdd3064f5a52bbd471d8e5af7811)
![{\displaystyle \ \Rightarrow [\nabla \times \mathbf {E} ]=-{\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b636a33b8731766b512b004e9d23e5353a1b36ba)



![{\displaystyle \ (\nabla \cdot [\nabla \times \mathbf {E} ])={\frac {\partial \nabla \mathbf {B} }{\partial t}}=0\Rightarrow \nabla \mathbf {B} =g(x,y,z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7833938bc25dbebf2e4181d524659b253e4543a4)
