Дошка Гальтона

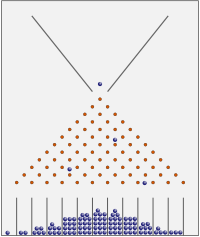
Дошка Гальтона

Рисунки Гальтона варіантів виконання приладу (1889)

До́шка Га́льтона (англ. Galton box), інші поширені назви квінкункс (англ. quincunx), машина Гальтона (англ. Galton machine) та англ. bean machine — пристрій, винайдений англійським вченим Френсісом Гальтоном (перший зразок було виготовлено у 1873 році, згодом описаний Гальтоном в книзі «Natural inheritance», виданій у 1889 році), що призначався для наглядного демонстрування центральної граничної теореми.

Будова пристрою

Пояснення до розрахунку ймовірностей потрапляння кульок у різні стовпці

Приклад виконання дошки Гальтона

Дошка Гальтона має вигляд ящика з прозорою передньою стінкою. В задню стінку в шаховому порядку вбиті штирі, що розташовані по площі, яка має форму трикутника, з вершиною, спрямованою вгору. Згори в ящик через лійку (вихід з якої розташований точно посередині між лівою і правою стінками) кидаються кульки. В ідеальному випадку стикаючись з штирем, кулька кожен раз з однаковою ймовірністю може повернути або праворуч, або ліворуч. Нижня частина ящика розділена перегородками (число яких дорівнює числу штирів у нижньому ряду), в результаті чого кульки, падаючи на дно ящика, утворюють стовпчики, які є тим вищими, чим ближче стовпчик розташований до середини дошки (при досить великій кількості кульок крива, що огинає вершини стовпчиків наближається до кривої нормального розподілу).

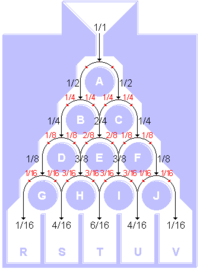
Якщо зобразити на задній стінці трикутник Паскаля, то можна побачити, скількома шляхами можна добратись до кожного із штирів (чим ближчим є штир до центру, тим більшою є кількість шляхів).

В деяких настільних іграх, а також в японському ігровому автоматі Патінко, використовується дошка Гальтона або схожі з нею пристрої.

Розподіл кульок

Позначимо як n загальну кількість зіткнень кульки зі штирями; за k число разів, коли кулька повертає праворуч (таким чином, він опиняється в k-му за порядком стовпці). Тоді кількість варіантів шляхів, якими він може добратись до k-го стовпця, визначається біноміальним коефіцієнтом ${n \choose k}$. Звідси випливає, що ймовірність опинитись в k-му стовпці дорівнює

${n \choose k}p^{k}(1-p)^{n-k}$,

де p — ймовірність повороту праворуч (зазвичай вважається, що $p=0,5$).

Це функція ймовірностей біноміального розподілу, який згідно з центральною граничною теоремою при достатньо великому n апроксимує нормальний розподіл.

Див. також

• Трикутник Паскаля

Посилання

• Нормальний розподіл. Дошка Гальтона (рос.)
• Відео, що демонструє роботу пристрою(англ.)
• Симуляція на сайті університету Джона Керрола(англ.)
• Quincunx and its relationship to normal distribution(англ.)
• The Bean Machine and the Central Limit Theorem (анімація)(англ.)
• Galton game (англ.)