Парадокс драбини
Парадокс драбини (або Парадокс комори та жердини) — це уявний експеримент в рамках спеціальної теорії відносності. В ньому розглядають драбину, яка рухається паралельно до землі і тому підлягає лоренцевому скороченню довжини. В результаті драбина може вміститись у гараж, для якого в звичайних умовах вона була б завеликою. З іншого боку, з точки зору спостерігача, що рухається разом з драбиною, саме драбина перебуває в стані спокою, а гараж перебуває в русі. Отже скоротиться довжина гаража і він не зможе вмістити драбину, оскільки й так був для неї замалим. Уявний парадокс виникає через помилкове припущення про абсолютну одночасність. Драбина поміщається в гараж лише якщо обидва її кінці одночасно перебувають всередині гаража. У релятивістиці одночасність відносна для кожного спостерігача, тому питання про те, чи перебуває драбина в гаражі, необхідно розглядати щодо кожного спостерігача і таким чином можна вирішити парадокс.
У найпростішій версії парадоксу є гараж з відкритими дверима спереду і позаду, а також драбина, яка є занадто довгою щоб уміститись у гараж, якщо вона перебуває в стані спокою відносно нього. Тепер ми починаємо рухати драбину крізь гараж із високою горизонтальною швидкістю. Через високу швидкість драбина підлягає ефекту скорочення довжини, і стає значно коротшою. В результаті цього, пролітаючи через гараж, драбина протягом певного часу повністю поміщається всередині нього. Щоб це показати, ми могли б одночасно закрити обидві двері гаража на короткий час, щоб показати, що драбина перебуває всередині.
Дотепер не було жодного парадоксу. Він виникає тоді, коли ми розглянемо той самий ефект з точки зору гаража. Оскільки спостерігач на драбині рухається з постійною швидкістю відносно інерціальної системи відліку гаража, то система відліку цього спостерігача також інерціальна. А отже, згідно з принципом відносності, для системи відліку драбини справедливі ті самі закони фізики. З точки зору нашого спостерігача, драбина стоїть на місті, а гараж навпаки летить на нього з високою швидкістю. Отже, скорочується довжина гаража і можна зробити висновок, що при прольоті драбини гараж не може її повністю вмістити. Таким чином ми не можемо закрити двері гаража з обох сторін. У цій суперечності й полягає суть парадоксу.
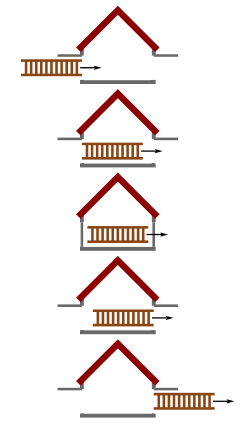
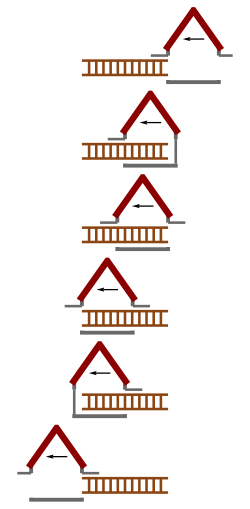
Секрет розв'язання парадоксу лежить у відносності одночасності: все, що здається одночасним спостерігачеві в одній системі відліку (наприклад, гаража), може бути неодночасним спостерігачеві в іншій системі відліку (в нашому випадку драбини). Коли ми говоримо, що драбина «поміщається» в гараж, насправді ми маємо на увазі, що і передній і задній кінці драбини перебувають всередині гаража. Іншими словами, обидва кінці драбини перебувають в гаражі одночасно. Оскільки одночасність відносна, у двох різних системах відліку драбина може як поміститися, так і не поміститися, причому спостерігачі в обох системах будуть праві. З точки зору спостерігача в гаражі, передня і задня частина драбини в якийсь момент одночасно перебували всередині гаража, тому драбина поміщається. Однак з точки зору спостерігача на драбині ці події відбулися не одночасно, і гараж не вмістив її.
Це легко побачити, якщо розглянути таку ситуацію. В системі відліку гаража двері одночасно на короткий час закриваються, як тільки драбина повністю увійде в гараж. Тепер розглянемо цю подію в системі відліку драбини. Спочатку передня частина драбини досягає задніх дверей гаража. Ці двері зачиняються, а потім відчиняються, давши жердини можливість пролетіти наскрізь. Через деякий час до вхідних дверей гаража долітає задній кінець драбини, і, в свою чергу, зачиняються і відчиняються передні двері. Звідси видно, що оскільки одночасність відносна, то двері не обов'язково мають бути закритими одночасно, і драбині не потрібно повністю поміщатися в гараж.
Доброю ілюстрацією до цієї ситуації є наведена нижче діаграма Мінковського. Вона побудована в системі відліку гаража. Вертикальний блакитний діапазон показує простір-час гаража, червоний — драбини. x і t позначають простір і час гаража, відповідно x' і t' — драбини.
В системі відліку гаража в кожен момент часу драбина зображена на діаграмі набором точок у вигляді горизонтальної лінії, що проходить паралельно осі x всередині червоного діапазону. Жирна синя лінія, що лежить в синьому сегменті гаража, зображає драбину в момент, коли вона повністю перебуває в гаражі. Однак у системі відліку драбини одночасні події розташовані по лініях, які паралельні до осі x'. Таким чином, положення драбини в будь-який момент часу виражене перетином цих ліній з червоним сегментом. Згідно зі схемою, жирна червона лінія ніколи повністю не лежить у синьому діапазоні, а отже, драбина ніколи повністю не перебуває в гаражі.

- Wells, Willard H. (1961). Length paradox in relativity. American Journal of Physics. 29 (12): 858—858. Bibcode:1961AmJPh..29..858W. doi:10.1119/1.1937641.
- Shaw, R. (1962). Length contraction paradox. American Journal of Physics. 30 (1): 72—72. Bibcode:1962AmJPh..30...72S. doi:10.1119/1.1941907.
- Martins, Roberto De A. (1978). Length paradox in relativity. American Journal of Physics. 46 (6): 667—670. Bibcode:1978AmJPh..46..667M. doi:10.1119/1.11227.
- Sastry, G. P. (1987). Is length contraction really paradoxical?. American Journal of Physics. 55 (10): 943—946. Bibcode:1987AmJPh..55..943S. doi:10.1119/1.14911.
- Grøn, Øyvind; Johannesen, Steinar (1993). Computer simulation of Rindler's length contraction paradox. European Journal of Physics. 14 (3): 97—100. Bibcode:1993EJPh...14...97G. doi:10.1088/0143-0807/14/3/001.
- van Lintel, Harald; Gruber, Christian (2005). The rod and hole paradox re-examined. European Journal of Physics. 26 (1): 19—23. Bibcode:2005EJPh...26...19V. doi:10.1088/0143-0807/26/1/003.
- Iyer, Chandru; Prabhu, G. M. (2008). Reversal in the time order of interactive events: the collision of inclined rods. European Journal of Physics. 27 (4): 819—824. arXiv:0809.1721. Bibcode:2006EJPh...27..819I. doi:10.1088/0143-0807/27/4/013.
- Pierce, Evan (2007). The lock and key paradox and the limits of rigidity in special relativity. American Journal of Physics. 75 (7): 610—614. Bibcode:2007AmJPh..75..610P. doi:10.1119/1.2711827.
- Iyer, Chandru; Prabhu, G. M. (2008). Differing observations on the landing of the rod into the slot. American Journal of Physics. 74 (11): 998—1001. arXiv:0809.1740. Bibcode:2006AmJPh..74..998I. doi:10.1119/1.2346686.
- McGlynn, Enda; van Kampen, Paul (2008). A note on linking electric current, magnetic fields, charges and the pole in a barn paradox in special relativity. European Journal of Physics. 29 (6): N63—N67. Bibcode:2008EJPh...29...63M. doi:10.1088/0143-0807/29/6/N03.
- Edwin F. Taylor and John Archibald Wheeler, Spacetime Physics (2nd ed) (Freeman, NY, 1992)
- Rindler, Wolfgang (2001). Relativity: Special, General and Cosmological. Oxford University Press. ISBN 0-19-850836-0.
- Ferraro, Rafael (2007). Einstein's space-time: an introduction to special and general relativity. Springer. ISBN 978-0-387-69946-2.



