Симетрична різниця множин

Діаграма Ейлера — Венна для симетричної різниці

Теоретико-множинні операції

${\overline {A}}\!$ доповнення

$A\cup B\!$ об'єднання
$A\cap B\!$ перетин

$A\setminus B\!$ різниця

$A\triangle B\!$ симетрична різниця
$A\times B\!$ декартів добуток

Симетрична різниця двох множин — теоретико-множинна операція, результатом якої є нова множина, що включає всі елементи вихідних множин, які не належать одночасно обом вихідним множинам. Іншими словами, якщо є дві множини A і B, їх симетрична різниця є об'єднання елементів A, що не входять в B, з елементами B не членами A. На письмі для позначення симетричної різниці множин A і B використовується позначення A △ B.

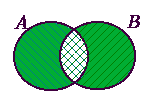
В математиці та теорії множин, симетричною різницею двох множин є така множина елементів, які містяться в одній з цих двох множин, але не в обох.

Визначення

Симетричну різницю можна визначити двома способами:

• симетрична різниця двох заданих множин А та В — це така множина A △ B, куди входять всі ті елементи першої множини, які не входять в другу множину, а, також ті елементи другої множини, які не входять в першу множину:

$(A\triangle B)=(A\setminus B)\cup (B\setminus A)$

• симетрична різниця двох заданих множин A і B — це така множина A △ B, куди входять всі ті елементи обох множин, які не є загальними для двох заданих множин.

$(A\triangle B)=(A\cup B)\setminus (A\cap B)$

Властивості

• Симетрична різниця є бінарною операцією у будь-якому булеані;
• Симетрична різниця є комутативною: $A\bigtriangleup B=B\,\triangle \,A;$
• Симетрична різниця є асоціативною: $\left(A\bigtriangleup B\right)\,\triangle \,C=A\bigtriangleup \left(B\,\triangle \,C\right);$
• Перетин множин  є дистрибутивним відносно симетричної різниці: $A\cap \left(B\bigtriangleup C\right)=\left(A\cap B\right)\bigtriangleup \left(A\cap C\right);$
• Порожня множина є нейтральним елементом симетричної різниці:  $A\bigtriangleup \varnothing =A;$
• Будь-яка множина обернена сама собі відносно операції симетричної різниці: $A\bigtriangleup A=\varnothing ;$
• Булеан з операцією симетричної різниці є абелевою групою;
• $\left(A_{1}\cap A_{2}\right)\bigtriangleup \left(B_{1}\cap B_{2}\right)\subset \left(A_{1}\bigtriangleup B_{1}\right)\cup \left(A_{2}\bigtriangleup B_{2}\right);$
• $\left(A_{1}\cup A_{2}\right)\bigtriangleup \left(B_{1}\cup B_{2}\right)\subset \left(A_{1}\bigtriangleup B_{1}\right)\cup \left(A_{2}\bigtriangleup B_{2}\right);$
• $\left(A_{1}\setminus A_{2}\right)\bigtriangleup \left(B_{1}\setminus B_{2}\right)\subset \left(A_{1}\bigtriangleup B_{1}\right)\cup \left(A_{2}\bigtriangleup B_{2}\right);$
• Об'єднання симетричної різниці з перетином двох множин дорівнює об'єднанню вихідних множин $(A\bigtriangleup B)\cup (A\cap B)=A\cup B$;
• Між симетричною різницею та об'єднанням множин такий зв'язок:

$A\triangle B=(A\setminus B)\cup (B\setminus A)$

• Зв'язок з операцією перетину множин такий:

$(A\triangle B)=(A\cup B)\setminus (A\cap B)$

Приклади

Симетрична різниця AΔB

1. Нехай

$A=\{1,2,3,4,5\},\quad B=\{3,4,5,6,7\}.$

Тоді

$A\,\triangle \,B=\{1,2,6,7\}.$

2. Симетрична різниця множини усіх студентів та усіх осіб жіночої статі, містить множину усіх студентів-чоловіків та усіх жінок, які не є студентами.

Дивитися також

• Множина
• Базис циклів

Література

• Куратовский К., Мостовский А. Теория множеств = Set Theory (Teoria mnogości). — М. : Мир, 1970. — 416 с.(рос.)