Розподіл Райса

Розподіл Райса є узагальненням розподілу Рейлі. Введено американським ученим Стефаном Райсом.

Якщо ${X}$ і ${Y}$ - незалежні випадкові величини, що мають нормальний розподіл з однаковими дисперсіями ${\sigma }^{2}$ і ненульовими математичними сподіваннями (у загальному випадку нерівними), то величина $Z={\sqrt {X^{2}+Y^{2}}}$ має розподіл Райса, щільність імовірності якої визначається у виді

$f(x|\nu ,\sigma )={\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right),$

де І₀(z) - модифікована функція Бесселя нульового порядку.

Щільність розподілу Райса при σ = 1.0


Щільність розподілу Райса для σ = 0.25


Функція розподілу Райса при σ = 1.0


Функція розподілу Райса при σ = 0.25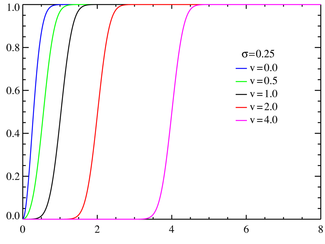

Застосування

• Розподіл Райса часто використовують для опису амплітудних флуктуацій радіосигналу, у тому числі в багатопроменевих каналах поширення радіосигналу.

Зв'язок з іншими розподілами

• Якщо ${X}$ і ${Y}$ - незалежні випадкові величини, що мають нормальний розподіл з нульовими математичними чеканнями й однаковими дисперсіями ${{\sigma }^{2}}$, те випадкова величина $Z={\sqrt {{{X}^{2}}+{{Y}^{2}}}}$ має розподіл Релея.

Див. також

• Розподіл Рейлі