Розподіл Леві

Леві
Функція розподілу ймовірностей
Параметри	$\mu$ ; $c>0\,$
Носій функції	$x\in [\mu ,\infty )$
Розподіл імовірностей	${\sqrt {\frac {c}{2\pi }}}~~{\frac {e^{-{\frac {c}{2(x-\mu )}}}}{(x-\mu )^{3/2}}}$
Функція розподілу ймовірностей (cdf)	${\textrm {erfc}}\left({\sqrt {\frac {c}{2(x-\mu )}}}\right)$
Середнє	$\infty$
Медіана	$c/2({\textrm {erfc}}^{-1}(1/2))^{2}\,$, for $\mu =0$
Мода	${\frac {c}{3}}$, for $\mu =0$
Дисперсія	$\infty$
Коефіцієнт асиметрії	undefined
Коефіцієнт ексцесу	undefined
Ентропія	${\frac {1+3\gamma +\ln(16\pi c^{2})}{2}}$ де $\gamma$ — Стала Ейлера—Маскероні
Твірна функція моментів (mgf)	невизначена
Характеристична функція	$e^{i\mu t-{\sqrt {-2ict}}}$

В теорії ймовірностей і математичній статистиці, розподіл Леві — неперервний розподіл ймовірностей для невід'ємної випадкової величини, названий на честь французького математика Поля Леві.

Цей розподіл є одним з кількох стійких розподілів, густина імовірності яких може бути записана аналітично. Іншими прикладами є нормальний розподіл і розподіл Коші.

Визначення

Густина імовірності розподілу Леві на множині $x\geq \mu$ визначається

$f(x;\mu ,c)={\sqrt {\frac {c}{2\pi }}}~~{\frac {e^{-{\frac {c}{2(x-\mu )}}}}{(x-\mu )^{3/2}}}$

де $\mu$ — параметр розміщення, $c$ — коефіцієнт масштабування. Функція розподілу ймовірностей:

$F(x;\mu ,c)={\textrm {erfc}}\left({\sqrt {c/2(x-\mu )}}\right)$

де ${\textrm {erfc}}(z)$ — доповнююча функція помилок. Параметр $\mu$ зміщує криву вправо на відстань $\mu$, змінюючи носій функції на множину [$\mu$, $\infty$). Як усі стійкі розподіли, розподіл Леві має стандартну форму f(x;0,1) з властивістю:

$f(x;\mu ,c)dx=f(y;0,1)dy\,$

де y визначено як

$y={\frac {x-\mu }{c}}\,$

Характеристична функція розподілу Леві визначається формулою:

$\varphi (t;\mu ,c)=e^{i\mu t-{\sqrt {-2ict}}}.$

Для $\mu =0$, the nth момент незміщеного розподілу Леві формально визначаються:

$m_{n}\ {\stackrel {\mathrm {def} }{=}}\ {\sqrt {\frac {c}{2\pi }}}\int _{0}^{\infty }{\frac {e^{-c/2x}\,x^{n}}{x^{3/2}}}\,dx$

Проте для всіх значень n > 0 інтеграл у формулі розбігається і моменти для розподілу є невизначеними. Твірна функція моментів формально визначається:

$M(t;c)\ {\stackrel {\mathrm {def} }{=}}\ {\sqrt {\frac {c}{2\pi }}}\int _{0}^{\infty }{\frac {e^{-c/2x+tx}}{x^{3/2}}}\,dx$

і розбігається для $t>0$ і, відповідно, теж не є визначеною.

Як і всі стійкі розподіли окрім нормального, для розподілу Леві характерний «важкий хвіст». Хвіст функції густини розподілу асимптотично поводиться як степенева функція:

$\lim _{x\rightarrow \infty }f(x;\mu ,c)={\sqrt {\frac {c}{2\pi }}}~{\frac {1}{x^{3/2}}}.$

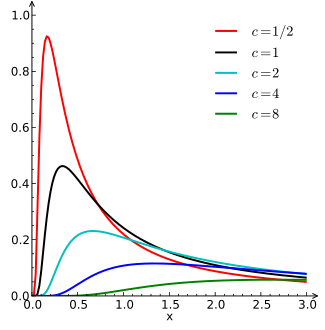
Це легко побачити на графіку де функції густини для різних значень c при $\mu =0$ показані в логарифмічному масштабі:

Функції густини розподілу Леві в лог-лог масштабі.

Пов'язані розподіли

• Якщо $X\sim {\textrm {Levy}}(\mu ,c)\,$ тоді $kX+b\sim {\textrm {Levy}}(k\mu +b,kc)\,$
• Якщо $X\,\sim \,{\textrm {Levy}}(0,c)$ тоді $X\,\sim \,{\textrm {Inv-Gamma}}({\tfrac {1}{2}},{\tfrac {c}{2}})$ (обернений гамма-розподіл)
• Розподіл Леві є частковим випадком розподілу Пірсона типу 5.
• Якщо $Y\,\sim \,{\textrm {Normal}}(\mu ,\sigma ^{2})$ (нормальний розподіл) тоді ${(Y-\mu )}^{-2}\sim \,{\textrm {Levy}}(0,1/\sigma ^{2})$
• Якщо $X\sim {\textrm {Normal}}(\mu ,{\tfrac {1}{\sqrt {\sigma }}})\,$ тоді ${(X-\mu )}^{-2}\sim {\textrm {Levy}}(0,\sigma )\,$
• Якщо $X\,\sim \,{\textrm {Levy}}(\mu ,c)$ тоді $X\,\sim \,{\textrm {Stable}}(1/2,1,c,\mu )\,$ (Стійкий розподіл)
• Якщо $X\,\sim \,{\textrm {Levy}}(0,c)$ тоді $X\,\sim \,{\textrm {Scale-inv-}}\chi ^{2}(1,c)$ (Масштабований обернений розподіл хі-квадрат)

Див. також

• Політ Леві

Посилання

• Information on stable distributions. Архів оригіналу за 22 липня 2013. Процитовано July 6 2012. Особливо An introduction to stable distributions, Chapter 1 [Архівовано 17 липня 2011 у Wayback Machine.]