Розподіл Парето
| Розподіл Парето | |
|---|---|
|
Щільність розподілу  Функції щільності розподілу Парето типу I для різних при При тому як розподіл наближається до де це Дельта-функція Дірака. | |
|
Функція розподілу ймовірностей  Кумулятивна функція розподілу Парето типу 1 для різних при | |
| Параметри |
масштаб (дійсне) параметр форми (дійсне) |
| Носій функції | |
| Розподіл імовірностей | |
| Функція розподілу ймовірностей (cdf) | |
| Середнє | |
| Медіана | |
| Мода | |
| Дисперсія | |
| Коефіцієнт асиметрії | |
| Коефіцієнт ексцесу | |
| Ентропія | |
| Твірна функція моментів (mgf) | |
| Характеристична функція | |
Розподіл Парето в теорії імовірностей — двопараметрична сім'я абсолютно неперервних розподілів. Названий на честь італійського інженера з цивільного будівництва[en], економіста, і соціолога Вільфредо Парето. Це степеневий розподіл ймовірностей, який використовується для описання соціальних, наукових, геофізичних, актуарних, та багатьох інших типів спостережуваних явищ. Початково застосовувалася для описання розподілу багатства[en] серед суспільства, що відповідає тенденції, що велика частина багатства зосереджена в руках невеликої частини населення людей. У розмовній версії розподіл Парето відомий як принцип Парето, або "правило 80—20", а також іноді може називатися "ефектом Матвія". Це правило стверджує що, наприклад, 80% багатства суспільства утримують 20% його населення. Однак, розподіл Парето дає цей результат тільки при певному значенні степеня, (α = log45 ≈ 1.16). Хоча є змінною, емпіричні спостереження установили, що розподіл 80-20 відповідає широкому загалу випадків, включаючи природні явища і діяльність людини.
Визначення[ред. | ред. код]
Якщо X є випадковою величиною із розподілом Парето (Типу I),[1] тоді імовірність того, що X є більшою за деяке число x, тобто функція виживання[en] (іноді називається функцією надійності), визначається як
де xm де (обов'язково додатне) мінімально можливе значення X, та α є додатнім параметром. Розподіл Парето типу I характеризується параметром масштабування xm і параметром форми α. Якщо розподіл використовують для моделювання розподілу багатства, тоді параметр α в даному контексті називають індексом Парето[en].
Властивості[ред. | ред. код]
Кумулятивна функція розподілу[ред. | ред. код]
Із визначення, кумулятивною функцією розподілу імовірностей випадкової величини Парето із параметрами α і xm є
Функція густини імовірностей[ред. | ред. код]
Звідси випливає (шляхом диференціювання) що функцією густини імовірностей є
При відображені на графіку, функція густини нагадує вигнуту криву, яка асимптотично наближається до кожної із осей. Всі сегменти кривої є самоподібними (з урахуванням відповідних коефіцієнтів масштабування). При зображенні на логарифмічному графіку, розподіл представляється у вигляді прямої лінії.
Моменти і характеристична функція[ред. | ред. код]
- Математичне сподівання випадкової величини, що має розподіл Парето визначається як
- Дисперсія випадкової величини, що відповідає розподілу Парето визначається як
- (Якщо α ≤ 1, дисперсія не існує.)
- Загальна формула для визначення моментів є наступною:
- Твірна функція моментів визначена лише для не додатних значень t ≤ 0, оскільки
- Характеристична функція випадкової величини визначається як
- де Γ(a, x) є неповною Гамма-функцією.
Умовний розподіл[ред. | ред. код]
Умовний розподіл імовірностей випадкової величини із розподілом Парето, задає подію що величина є більшою або рівною у порівнянні із певним числом , яке перевищує , є розподілом Парето із тим самим індексом Парето , але із мінімальним замість .
Характеристична теорема[ред. | ред. код]
Припустимо, що є незалежні однаково розподілені випадкові величини, розподіл імовірностей яких знаходиться в інтервалі supported для деякого значення . Припустимо, що для всіх , пара випадкових величин і є незалежними. Тоді їх спільний розподіл буде розподілом Парето.
Середнє геометричне[ред. | ред. код]
Середнє геометричне (G) визначається як:[2]
Середнє гармонійне[ред. | ред. код]
Середнє гармонійне (H) визначається як:[2]
Узагальнений розподіл Парето[ред. | ред. код]
Існує ієрархія [1][3] розподілів Парето, що відомі як Парето Тип I, II, III, IV, і розподіл Феллера–Парето.[1][3][4] Парето типу IV включає Парето типів I–III як особливі випадки. Розподіл Феллера–Парето[3][5] узагальнює Парето IV типу.
Парето I–IV типів[ред. | ред. код]
Ієрархія розподілів Парето узагальнена у наступній таблиці, яка порівнює функції виживання[en] (доповнена кумулятивна функція розподілу).
Коли μ = 0, розподіл Парето II типу відомий також як розподіл Ломакса.[6]
В даному розділі, символ xm, що використовується для позначення мінімального значення x, замінено на символ σ.
| Умова | Параметри | ||
|---|---|---|---|
| Тип I | |||
| Тип II | |||
| Ломакса | |||
| Тип III | |||
| Тип IV |
Параметр форми позначено як α, μ - положення, σ це масштаб, γ - параметр нерівності. Деякими особливими випадками розподілу Парето IV типу є:
Скінченність середнього значення, а також існування і скінченність дисперсії залежить від індексу α (індексу нерівності γ). Зокрема, часткові δ-моменти є скінченними для деяких δ > 0, як показано у таблиці нижче, де δ не обов'язково є цілим числом.
| Умова | Умова | |||
|---|---|---|---|---|
| Тип I | ||||
| Тип II | ||||
| Тип III | ||||
| Тип IV |
Розподіл Феллера–Парето[ред. | ред. код]
Феллер[3][5] визначає змінну Парето шляхом перетворення U = Y−1 − 1 випадкової величини Y із Бета-розподілом, функція густини розподілу якої дорівнює
де B( ) - Бета-функція. Якщо
тоді W має розподіл Феллера–Парето FP(μ, σ, γ, γ1, γ2).[1]
Якщо і є незалежними Гамма-розподіленими величинами, іншим способом побудувати випадково величину із розподілом Феллера–Парето (ФП) можна як[7]
і ми запишемо W ~ FP(μ, σ, γ, δ1, δ2). Особливими випадками розподілу Феллера–Парето є
Застосування[ред. | ред. код]
Парето спочатку застосував цей розподіл для моделювання розподілу багатства[en] між людьми оскільки здавалося він досить добре показує те, що більша частина багатства будь-якого суспільства як правило зосереджена у власності невеликого проценту осіб із даного суспільства. Він також використовував її для описання розподілу прибутку.[8] Цю ідею як правило описують в більш простій формі як принцип Парето або "правило 80—20" яке стверджує, що 20% населення контролюють 80% всіх багатств.[9] Однак, правило 80-20 відповідає частковому значенню α, і на справді, дані Парето про податки на прибуток в Британії в його роботі Cours d'économie politique вказують, що близько 30% населення мали близько 70% прибутку. Графік функції густини імовірності на початку цієї статті показу, що "імовірність" або частка населення, яка володіє невеликою кількістю багатства на людину, є досить великою, і зменшується зі зростанням кількості багатства. (Слід зауважити, що розподіл Парето не є реалістичним для випадку із невеликою величиною багатства. Насправді, чисті активи можуть бути навіть від'ємними.) Цей розподіл не обмежується використанням для описання багатства або прибутку населення, а і використовується для багатьох ситуацій, в яких знаходиться рівновага у розподіленні від "малого" до "великого". Наступні прикладі іноді розглядають як такі, що приблизно мають розподіл Парето:
- Розмір населених пунктів (небагато міст, багато селищ/сіл)[10]
- Розподіл розмірів файлів в Інтернет-трафіку в якому використовується протокол TCP (багато менших файлів, рідше великі)[10]
- Частота помилок запису на жорсткому диску[11]
- Кластери конденсації Бозе — Ейнштейна близько абсолютного нуля[12]
- Величина запасів нафти в нафтових родовищах (не багато великих родовищ[en], і багато малих родовищ)[10]
- Обсяг задач, які виносилися для вирішення на суперкомп'ютерах (декілька великих, багато малих)[13]
- Нормалізована дохідність цін на окремі акції.[10]
- Розміри частинок піску [10]
- Розмір метеоритів
- Величина значних втрат унаслідок катастроф для певного роду бізнесу, генеральні зобов'язання, комерційні авто, і компенсація робітникам.[14][15]
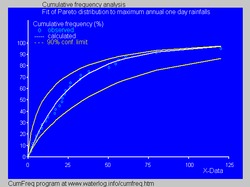
- В Гідрології розподіл Парето застосовується для моделювання надзвичайних подій таких як щорічні максимальні опади на добу і паводок рік.[16] Зображення із синім фоном показує приклад підбору розподілу Парето для впорядкованого показнику щорічного максимуму опадів на добу показує також 90% довірчий інтервал оснований на біноміальному розподілі. Дані випадіння опадів показані за допомогою точкових позицій, що зрештою показує процес кумулятивний частотний аналіз.
Зв'язок із іншими розподілами[ред. | ред. код]
Зв'язок із експоненційним розподілом[ред. | ред. код]
Розподіл Парето пов'язаний із експоненційним розподілом наступним чином. Якщо випадкова величина X має розподіл Парето із мінімумом xm і індексом α, тоді
є експоненційно розподіленою величиною із параметром α. Аналогічно, якщо Y експоненційно розподілена випадкова величина із параметром α, тоді
має розподіл Парето із мінімумом xm та індексом α.
Це можна використовувати у стандартній процедурі заміни змінної:
Крайній вираз задає кумулятивну функцію розподілу для експоненційного розподілу із параметром α.
Зв'язок із узагальненим розподілом Парето[ред. | ред. код]
Розподіл Парето є особливим випадком узагальненого розподілу Парето, який є сімейством розподілів подібної форми, але містить додатковий параметр, що дозволяє обмежити розподіл знизу (в довільній точці), або бути обмеженим зверху і знизу (де обидві межі є змінними), і містить розподіл Ломакса як особливий випадок. До цього сімейства відносяться також обидва зміщений і не зміщений експоненційні розподіли.
Розподіл Парето із масштабом і формою еквівалентний узагальненому розподілу Парето із зсувом , масштабом і формою . І навпаки, можна отримати розподіл Парето із узагальненого розподілу Парето прийнявши, що і .
Зв'язок із законом Ципфа[ред. | ред. код]
Розподіл Парето є неперервним розподілом ймовірностей.Закон Ципфа, який іноді називають дзета-розподілом, це дискретний розподіл, який розділяє величини на просте ранжування. Обидва є простим степеневим законом із від'ємним показником, масштабовані так, що їхня кумулятивна функція розподілу дорівнює 1. Розподіл Ципфа можна отримати із розподілу Парето якщо значення (прибутки) ранговані на класів, так що кількість людей в кожному класі визначається відповідно до відношення 1/ранг. Розподіл нормалізують шляхом визначення такого , що де є узагальненим гармонічним числом. Це дозволяє отримати функцію густини імовірностей для розподілу Ципфа із розподілу Парето.
де і є цілим числом, що задає ранг від 1 до N де N є найвищим доходом. Таким чином довільно обрана особа (або слово, посилання на вебсайт, або місто) із популяції (або мови, інтернету, чи країни) має ймовірність ранжування .
Зв'язок із "Принципом Парето"[ред. | ред. код]
"Правило 80—20", відповідно до якого 20% всіх людей отримують 80% всього прибутку, і 20% з найбільш забезпечених 20% отримують 80% із тих 80%, і так далі, точно дотримується якщо індекс Парето становить α = log4(5) = log(5)/log(4), приблизно 1.161. Цей результат можна отримати із формули для розподілу Лоренца наведеної нижче. Крім того, було показано що наступні твердження[17] є математично еквівалентними:
- Прибуток розподіляється відповідно до розподілу Парето з індексом α > 1.
- Існує деяке число 0 ≤ p ≤ 1/2 таке що 100p % з усіх людей отримують 100(1 − p)% всього прибутку, і аналогічно для кожного дійсного числа (не обов'язково цілого) n > 0, 100pn % з усіх людей отримують 100(1 − p)n процентів всього доходу. α і p пов'язані між собою наступним чином
Це відноситься не тільки до прибутку, а і до багатства, або будь-чого що може моделювати цей розподіл.
Це включає також розподіли Парето що мають 0 < α ≤ 1, які, як було вказано вище, мають нескінченне математичне сподівання і таким чином не можуть достовірно моделювати розподіл прибутку.
Розподіл Лоренца і коефіцієнт Джині[ред. | ред. код]
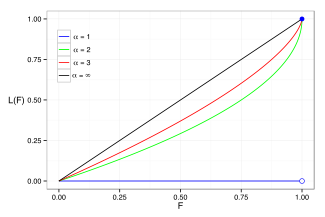
Розподіл Лоренца часто використовують для характеристики розподілу доходів і багатства. Для будь-якого розподілу, розподіл Лоренца L(F) можна записати через функцію щільності f або функцію розподілу F як
де x(F) є оберненою для функції розподілу CDF. Для розподілу Парето,
а крива Лоренца розраховується як
Для знаменник буде нескінченним, що приводить до L=0. Приклади кривої Лоренца для декількох розподілів Парето показані на малюнку праворуч.
Відповідно до Оксфам (2016) найбагатші 62 людини мають стільки ж статку як найбідніша половина світової популяції.[18] Ми можемо розрахувати індекс Парето, який відповідатиме цій ситуації. Прийнявши, що ε дорівнює маємо:
або
В результаті α дорівнює близько 1.15, і близько 9% з усіх статків належать кожній з цих груп. Але насправді найбідніші 69% із дорослих людей всього світу володіють лише близько 3% статків.[19]
Коефіцієнт Джині є мірою відхилення кривої Лоренца від рівнорозподіленої прямої, що є прямою яка сполучає точки [0, 0] і [1, 1], яка на графіку праворуч показана чорним кольором (α = ∞). Конкретно, коефіцієнт Джині є подвоєною площею між кривою Лоренца і рівнорозподіленою прямою. Коефіцієнт Джині для розподілу Парето розраховується (для ) як
Оцінка параметрів[ред. | ред. код]
Функція правдоподібності для параметрів α і xm розподілу Парето, для незалежної вибірки x = (x1, x2, ..., xn), задається як
Таким чином, логарифмічна функція правдоподібності дорівнює
Можна побачити, що монотонно зростає із зростанням xm, таким чином, чим більшим є значення xm, тим більшим буде значення функції правдоподібності. Таким чином, оскільки x ≥ xm, ми можемо зробити висновок, що
Для того, щоб знайти статистичну оцінку для α, ми розраховуємо відповідну часткову похідну і знаходимо де вона дорівнює нулю:
Таким чином, оцінкою максимальної правдоподібності для α буде:
Очікувана статистична оцінка дорівнює:[20]
Малік (1970)[21] приводить результат із точним спільним розподілом величин . Зокрема, і є незалежними а має розподіл Парето із параметром масштабу xm і параметром форми nα, тоді як має Обернений гамма-розподіл із параметрами форми і масштабу n − 1 та nα, відповідно.
Графічне представлення[ред. | ред. код]
Характерна крива розподілу із 'довгим хвостом' при зображенні на лінійній шкалі, приховує в собі внутрішню простоту функції при зображенні її у логарифмічній системі координат, де вона приймає форму прямої лінії із від'ємним градієнтом: Із формули для функції густини імовірностей випливає, що для x ≥ xm,
Оскільки α є додатнім, градієнт −(α + 1) є від'ємним.
Генерування випадкової вибірки[ред. | ред. код]
Генерування випадкової вибірки можна виконати за допомогою зворотного перетворення[en]. Дано випадкову величину U, яка отримана із неперервного рівномірного розподілу у одиничному інтервалі (0, 1], змінна T задана виразом
маж розподіл Парето.[22] Якщо U неперервно рівномірно розподілена у інтервалі [0, 1), її можливо замінити на (1 − U).
Варіанти[ред. | ред. код]
Обмежений розподіл Парето[ред. | ред. код]
| Обмежений розподіл Парето | |
|---|---|
| Параметри |
зсув (дійсне число) |
| Носій функції | |
| Розподіл імовірностей | |
| Функція розподілу ймовірностей (cdf) | |
| Середнє | |
| Медіана | |
| Дисперсія | (це момент другого порядку, не дисперсія) |
| Коефіцієнт асиметрії |
(це момент k-го порядку, не скошеність) |
Обмежений (або обрізаний) розподіл Парето має три параметри: α, L і H. Як і в стандартному розподілі Парето параметр α визначає форму. L означає мінімальне значення, а H позначає максимальне значення.
Функція густини імовірностей є наступною:
- ,
де L ≤ x ≤ H, і α > 0.
Генерування випадкових величин обмеженого розподілу Парето[ред. | ред. код]
Якщо U is рівномірно розподілена в інтервалі (0, 1), тоді застосувавши метод зворотнього перетворення, отримаємо [23]
є відповідає обмеженому розподілу Парето.
Симетричний розподіл Парето[ред. | ред. код]
Симетричний розподіл Парето можна визначити за допомогою наступної функції густини імовірностей:[24]
Він має форму подібну до розподілу Парето при x > xm є симетричним відображенням[en] відносно вертикальної осі.
Див. також[ред. | ред. код]
Джерела[ред. | ред. код]
- Карташов М. В. Імовірність, процеси, статистика. — Київ : ВПЦ Київський університет, 2007. — 504 с.
- Гнеденко Б. В. Курс теории вероятностей. — 6-е изд. — Москва : Наука, 1988. — 446 с.(рос.)
- Гихман И. И., Скороход А. В., Ядренко М. В. Теория вероятностей и математическая статистика. — Київ : Вища школа, 1988. — 436 с.(рос.)
- Hazewinkel, Michiel, ред. (2001), Pareto distribution, Математична енциклопедія, Springer, ISBN 978-1-55608-010-4
- Weisstein, Eric W. Pareto distribution(англ.) на сайті Wolfram MathWorld.
- Aabergé, Rolf (May 2005), Gini's Nuclear Family (PDF), архів оригіналу (PDF) за 20 квітня 2020, процитовано 5 березня 2019
- Crovella, Mark E.; Bestavros, Azer (December 1997). Self-Similarity in World Wide Web Traffic: Evidence and Possible Causes (PDF). IEEE/ACM Transactions on Networking. Т. 5, № 6. с. 835—846. Архів оригіналу (PDF) за 4 березня 2016. Процитовано 5 березня 2019.
- syntraf1.c [Архівовано 10 лютого 2019 у Wayback Machine.] - програма на мові програмування C для генерування штучного трафіку пакетів, із обмеженим розміром пакетів і часом між пакетами відповідно до розподілу Парето.
Примітки[ред. | ред. код]
- ↑ а б в г Barry C. Arnold (1983). Pareto Distributions. International Co-operative Publishing House. ISBN 978-0-89974-012-6.
- ↑ а б Johnson NL, Kotz S, Balakrishnan N (1994) Continuous univariate distributions Vol 1. Wiley Series in Probability and Statistics.
- ↑ а б в г Johnson, Kotz, and Balakrishnan (1994), (20.4).
- ↑ Christian Kleiber & Samuel Kotz (2003). Statistical Size Distributions in Economics and Actuarial Sciences. Wiley. ISBN 978-0-471-15064-0. Архів оригіналу за 20 квітня 2020. Процитовано 6 березня 2019.
- ↑ а б Feller, W. (1971). An Introduction to Probability Theory and its Applications. Т. II (вид. 2nd). New York: Wiley. с. 50. "The densities (4.3) are sometimes called after the economist Pareto. It was thought (rather naïvely from a modern statistical standpoint) that income distributions should have a tail with a density ~ Ax−α as x → ∞."
- ↑ Lomax, K. S. (1954). Business failures. Another example of the analysis of failure data. Journal of the American Statistical Association. 49 (268): 847—52. doi:10.1080/01621459.1954.10501239.
- ↑ Chotikapanich, Duangkamon. Chapter 7: Pareto and Generalized Pareto Distributions. Modeling Income Distributions and Lorenz Curves. с. 121—22. Архів оригіналу за 20 квітня 2020. Процитовано 6 березня 2019.
- ↑ Pareto, Vilfredo, Cours d'Économie Politique: Nouvelle édition par G.-H. Bousquet et G. Busino, Librairie Droz, Geneva, 1964, pp. 299–345.
- ↑ For a two-quantile population, where approximately 18% of the population owns 82% of the wealth, the Theil index takes the value 1.
- ↑ а б в г д Reed, William J. та ін. (2004). The Double Pareto-Lognormal Distribution – A New Parametric Model for Size Distributions. Communications in Statistics – Theory and Methods. 33 (8): 1733—53. CiteSeerX 10.1.1.70.4555. doi:10.1081/sta-120037438.
- ↑ Schroeder, Bianca; Damouras, Sotirios; Gill, Phillipa (24 лютого 2010). Understanding latent sector error and how to protect against them (PDF). 8th Usenix Conference on File and Storage Technologies (FAST 2010). Архів оригіналу (PDF) за 11 січня 2011. Процитовано 10 вересня 2010.
We experimented with 5 different distributions (Geometric,Weibull, Rayleigh, Pareto, and Lognormal), that are commonly used in the context of system reliability, and evaluated their fit through the total squared differences between the actual and hypothesized frequencies (χ2 statistic). We found consistently across all models that the geometric distribution is a poor fit, while the Pareto distribution provides the best fit.
- ↑ Yuji Ijiri; Simon, Herbert A. (May 1975). Some Distributions Associated with Bose–Einstein Statistics. Proc. Natl. Acad. Sci. USA. 72 (5): 1654—57. Bibcode:1975PNAS...72.1654I. doi:10.1073/pnas.72.5.1654. PMC 432601. PMID 16578724.
- ↑ Harchol-Balter, Mor; Downey, Allen (August 1997). Exploiting Process Lifetime Distributions for Dynamic Load Balancing (PDF). ACM Transactions on Computer Systems. 15 (3): 253—258. doi:10.1145/263326.263344. Архів оригіналу (PDF) за 20 квітня 2020. Процитовано 6 березня 2019.
- ↑ Kleiber and Kotz (2003): p. 94.
- ↑ Seal, H. (1980). Survival probabilities based on Pareto claim distributions. ASTIN Bulletin. 11: 61—71. doi:10.1017/S0515036100006620.
- ↑ CumFreq, software for cumulative frequency analysis and probability distribution fitting [1] [Архівовано 21 лютого 2018 у Wayback Machine.]
- ↑ Hardy, Michael (2010). Pareto's Law. Mathematical Intelligencer. 32 (3): 38—43. doi:10.1007/s00283-010-9159-2.
- ↑ 62 people own the same as half the world, reveals Oxfam Davos report. Oxfam. Jan 2016. Архів оригіналу за 20 жовтня 2019. Процитовано 7 березня 2019.
- ↑ Global Wealth Report 2013. Credit Suisse. Oct 2013. с. 22. Архів оригіналу за 14 лютого 2015. Процитовано 7 березня 2019.
- ↑ M. E. J. Newman (2005). Power laws, Pareto distributions and Zipf's law. Contemporary Physics. 46 (5): 323—51. arXiv:cond-mat/0412004. Bibcode:2005ConPh..46..323N. doi:10.1080/00107510500052444.
- ↑ H. J. Malik (1970). Estimation of the Parameters of the Pareto Distribution. Metrika. 15: 126—132. doi:10.1007/BF02613565.
- ↑ Tanizaki, Hisashi (2004). Computational Methods in Statistics and Econometrics. CRC Press. с. 133. ISBN 9780824750886. Архів оригіналу за 20 квітня 2020. Процитовано 6 березня 2019.
- ↑ Архівована копія. Архів оригіналу за 17 січня 2012. Процитовано 6 березня 2019.
{{cite web}}: Обслуговування CS1: Сторінки з текстом «archived copy» як значення параметру title (посилання) - ↑ Grabchak, M. & Samorodnitsky, D. Do Financial Returns Have Finite or Infinite Variance? A Paradox and an Explanation (PDF). с. 7—8. Архів оригіналу (PDF) за 11 липня 2012. Процитовано 7 березня 2019.











![{\displaystyle x_{\mathrm {m} }{\sqrt[{\alpha }]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef1a9e02a1d60cf9cd611b13188b078509904bc7)











![{\displaystyle \operatorname {D} (X)={\begin{cases}\infty &\alpha \in (1,2],\\\left({\frac {x_{\mathrm {m} }}{\alpha -1}}\right)^{2}{\frac {\alpha }{\alpha -2}}&\alpha >2.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1dfbf615c8b1b17f5bc5f7cedcb539d41840762)

![{\displaystyle M\left(t;\alpha ,x_{\mathrm {m} }\right)=\operatorname {E} \left[e^{tX}\right]=\alpha (-x_{\mathrm {m} }t)^{\alpha }\Gamma (-\alpha ,-x_{\mathrm {m} }t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b03963721b9c85e5030aa7a26056af4ef07a4e4)













![{\displaystyle \left[{\frac {x}{\sigma }}\right]^{-\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/debc11c1d4259755203a2e95e5171e4b2c28b695)


![{\displaystyle \left[1+{\frac {x-\mu }{\sigma }}\right]^{-\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1c05d4c866664355381925ebc7f1d6854a8b4b2)


![{\displaystyle \left[1+{\frac {x}{\sigma }}\right]^{-\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5f6d8660cc815594ad3f6fbbba08e57eaa4bf12)

![{\displaystyle \left[1+\left({\frac {x-\mu }{\sigma }}\right)^{1/\gamma }\right]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08d45a24039951a4a164feb7f48ee05c3b852a28)

![{\displaystyle \left[1+\left({\frac {x-\mu }{\sigma }}\right)^{1/\gamma }\right]^{-\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a95750fc2c1674af87b4f4d3115af6dbf9728743)




![{\displaystyle \operatorname {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44dd294aa33c0865f58e2b1bdaf44ebe911dbf93)
![{\displaystyle \operatorname {E} [X^{\delta }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fab8f72a2621c18717c6afbb3a3772ca30a36b4d)









































































