Розв'язування трикутників

Розв'язування трикутників (лат. solutio triangulorum) — історичний термін, що означає розв'язування головної тригонометричної задачі: за відомими даними про трикутник (сторони, кути і т. д.) знайти інші його характеристики. Існує також узагальнення цієї задачі на випадок, коли задані інші елементи трикутника (наприклад, медіани, бісектриси, висоти, площі та ін.). Трикутник може розташовуватися на площині або на сфері. Ця задача часто зустрічається, наприклад, в геодезії, астрономії, будівництві, навігації.

Розв'язування плоских трикутників

Стандартні позначення в трикутнику

У трикутника загального виду є 6 головних характеристик: 3 лінійні (довжини сторін $a,b,c$) і 3 кутові ($\alpha ,\beta ,\gamma$). Сторону, протилежну до кута при вершині, прийнято позначати тією ж літерою, що і вершину, але не великою, а малою (див. рисунок). В класичній задачі плоскої тригонометрії задано 3 з цих 6 характеристик, і потрібно визначити 3 інші. Очевидно, якщо відомі лише 2 або 3 кута, однозначного розв'язку не буде, оскільки будь-який трикутник, подібний до даного, також буде розв'язком, тому надалі вважається, що хоча б одна з відомих величин — лінійна.

Алгоритм розв'язування задачі залежить від того, які саме характеристики трикутника вважаються відомими. Надалі задані величини символічно позначаються С (сторона) і К (кут). Оскільки поєднання ККК не розглядається, залишається 5 різних варіантів:

• Три сторони (ССС);
• Дві сторони і кут між ними (СКС);
• Дві сторони і кут навпроти однієї з них (КСС);
• Сторона і два прилеглих кута (КСК);
• Сторона, протилежний кут і один з прилеглих (ККС).

Основні теореми

Стандартним методом розв'язування задачі є використання декількох фундаментальних співвідношень, що виконуються для всіх плоских трикутників:

Теорема косинусів

$a^{2}=b^{2}+c^{2}-2bc\cdot \cos \alpha$

$b^{2}=a^{2}+c^{2}-2ac\cdot \cos \beta$

$c^{2}=a^{2}+b^{2}-2ab\cdot \cos \gamma$

Сума кутів трикутника $\alpha +\beta +\gamma =180^{\circ },$ тобто розгорнутому куту.

Теорема синусів

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}$

Сума кутів трикутника

$\alpha +\beta +\gamma =180^{\circ }$

Із інших іноді корисних на практиці універсальних співвідношень слід згадати теорему тангенсів, теорему котангенсів і формули Мольвейде.

Зауваження

1. Для знаходження невідомого кута надійніше використовувати теорему косинусів, а не синусів. Причина в тому, що значення синуса кута при вершині трикутника не визначає однозначно самого кута. Наприклад, якщо $\sin \beta =0{,}5,$ то кут $\beta$ може бути як $30^{\circ }$, так і $150^{\circ }$, тому що синуси цих кутів рівні. Винятком є випадок, коли заздалегідь відомо, що в даному трикутнику тупих кутів бути не може — наприклад, якщо трикутник прямокутний. З косинусом такі проблеми не виникають, в інтервалі від $0^{\circ }$ до $180^{\circ }$ значення косинуса визначає кут однозначно.
2. При побудові трикутників важливо пам'ятати, що дзеркальне відбиття побудованого трикутника також буде розв'язком задачі. Наприклад, три сторони однозначно визначають трикутник з точністю до відбиття.
3. Всі трикутники вважаються невиродженими, тобто довжина сторони не може бути нульовою, а величина кута — додатне число, менше, ніж $180^{\circ }$.

Задано три сторони

Три сторони

Нехай задані довжини всіх трьох сторін $a,b,c$. Умова розв'язності задачі — виконання нерівності трикутника, тобто кожна довжина повинна бути меншою, ніж сума двох інших довжин:

$a<b+c;\;b<a+c;\;c<a+b$

Щоб знайти кути $\alpha ,\beta$, потрібно скористатися теоремою косинусів:

$\alpha =\arccos {\frac {b^{2}+c^{2}-a^{2}}{2bc}}$

$\beta =\arccos {\frac {a^{2}+c^{2}-b^{2}}{2ac}}$

Третій кут одразу знаходиться з правила, що сума всіх трьох кутів повинна бути рівна 180°:

$~\gamma =180^{\circ }-(\alpha +\beta )$.

Не рекомендується другий кут знаходити за теоремою синусів, тому що, як вказано у вищенаведеному зауваженні 1, при цьому є небезпека сплутати тупий кут із гострим. Цієї небезпеки не виникне, якщо першим визначити, за теоремою косинусів, найбільший кут, що лежить навпроти найбільшої із сторін — два інших кута точно є гострими, і застосування до них теореми синусів безпечне.

Ще один метод обчислення кутів за відомими сторонами — використання теореми котангенсів.

Задані дві сторони і кут між ними

Дві сторони і кут між ними

Нехай, для визначеності, відомі довжини сторін $a,b$ і кут $\gamma$ між ними. Цей варіант задачі завжди має єдиний розв'язок. Для визначення довжини сторони $c$ знову застосовується теорема косинусів:

$c={\sqrt {a^{2}+b^{2}-2ab\cos \gamma }}$

Фактично задача зведена до попереднього випадку. Далі ще раз застосовується теорема косинусів для знаходження другого кута:

$\alpha =\arccos {\frac {b^{2}+c^{2}-a^{2}}{2bc}}=\arccos {\frac {b-a\cos \gamma }{\sqrt {a^{2}+b^{2}-2ab\cos \gamma }}}$

Третій кут визначається з теореми про суму кутів трикутника: $\beta =180^{\circ }-\alpha -\gamma$.

Задані дві сторони і кут не між ними

Дві сторони і кут напроти однієї з них

У цьому випадку можуть існувати два розв'язки, єдиний розв'язок або взагалі не бути розв'язків. Нехай, наприклад, відомі дві сторони $b,c$ і кут $\beta$. Рівняння для кута $\gamma$ знаходиться з теореми синусів:

$\sin \gamma ={\frac {c}{b}}\sin \beta$

Для простоти позначимо $~D={\frac {c}{b}}\sin \beta$ (права частина рівняння). При розв'язуванні рівняння можливі 4 випадки.

1. Задача не має розв'язку (сторона $b$ «не дістає» до лінії BC) у двох випадках: якщо $D>1$ або якщо кут $\beta \geqslant 90^{\circ }$ і при цьому $b\leqslant c.$
2. Якщо $D=1$, існує єдиний розв'язок, причому трикутник прямокутний, $\gamma =90^{\circ }.$

Два можливих розв'язки

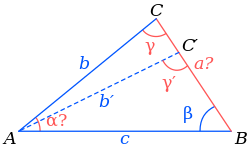
3. Якщо $D<1$, то можливі 2 варіанти.
   1. Якщо $b<c$, то кут $\gamma$ має два можливих значення: гострий кут $~\gamma =\arcsin D$ і тупий кут $~\gamma '=180^{\circ }-\gamma$. На рисунку справа першому значенню відповідає точка $C$, сторона $b$ і кут $\gamma$, а другому значенню — точка $C'$, сторона $b'=b$ і кут $\gamma '$.
   2. Якщо $b\geqslant c$, то $\beta \geqslant \gamma$ (як відомо, більшій стороні трикутника відповідає більший протилежний кут). Оскільки в трикутнику не може бути двох тупих кутів, тупий кут для $~\gamma$ виключений, і розв'язок $~\gamma =\arcsin D$ єдиний.

Третій кут визначається за формулою $~\alpha =180^{\circ }-\beta -\gamma$. Третю сторону можна знайти за теоремою синусів:

$a=b\ {\frac {\sin \alpha }{\sin \beta }}$

Задані сторона і прилеглі до неї кути

Сторона і два кути

Нехай задана сторона $c$ і два кути. Ця задача має єдиний розв'язок, якщо сума двох кутів менша $180^{\circ }$. У протилежному випадку задача розв'язку не має.

Спочатку визначається третій кут. Наприклад, якщо задані кути $\alpha ,\beta$, то $~\gamma =180^{\circ }-\alpha -\beta$. Далі обидві невідомі сторони знаходяться за теоремою синусів:

$a=c\ {\frac {\sin \alpha }{\sin \gamma }};\quad b=c\ {\frac {\sin \beta }{\sin \gamma }}$

Розв'язування прямокутних трикутників

Прямокутний трикутник

У цьому випадку відомий один з кутів — він дорівнює 90°. Необхідно знати ще два елементи, хоча б один з яких — сторона. Можливі наступні випадки:

• два катети;
• катет і гіпотенуза;
• катет і прилеглий гострий кут;
• катет і протилежний гострий кут;
• гіпотенуза і гострий кут.

Прийнято позначати вершину прямого кута літерою C, а гіпотенузу — $c$. Катети позначаються $a$ і $b$, а величини протилежних до них кутів — α і β відповідно.

Розрахункові формули суттєво спрощуються, оскільки замість теорем синусів і косинусів можна використати простіші співвідношення — теорему Піфагора:

$c^{2}=a^{2}+b^{2}$

і визначення основних тригонометричних функцій:

$\sin \alpha =\cos \beta ={\frac {a}{c}},\quad \cos \alpha =\sin \beta ={\frac {b}{c}},$

$\mathrm {tg} \alpha =\mathrm {ctg} \beta ={\frac {a}{b}},\quad \mathrm {ctg} \alpha =\mathrm {tg} \beta ={\frac {b}{a}}.$

Зрозуміло також, що кути α і β — гострі, оскільки їхня сума дорівнює $90^{\circ }$. Тому будь-який з невідомих кутів однозначно визначається за будь-якою з його тригонометричних функцій (синусом, косинусом, тангенсом та ін.) шляхом обчислення відповідної оберненої тригонометричної функції.

При коректній постановці задачі (якщо задані гіпотенуза і катет, то катет повинен бути меншим від гіпотенузи; якщо заданий один з двох непрямих кутів, то він повинен бути гострим) розв'язок завжди існує і єдиний.

Два катети

Гіпотенуза знаходиться за теоремою Піфагора:

$c={\sqrt {a^{2}+b^{2}}}.$

Кути можна знайти з використанням функції арктангенса:

$\alpha =\operatorname {arctg} \,{\frac {a}{b}},\quad \beta =\operatorname {arctg} \,{\frac {b}{a}}$

або ж за тільки що знайденою гіпотенузою:

$\alpha =\arcsin {\frac {a}{c}}=\arccos {\frac {b}{c}},\quad \beta =\arcsin {\frac {b}{c}}=\arccos {\frac {a}{c}}.$

Катет і гіпотенуза

Нехай відомі катет $b$ і гіпотенуза $c$, тоді катет $a$ знаходиться з теореми Піфагора:

$a={\sqrt {c^{2}-b^{2}}}.$

Після цього кути визначаються аналогічно до попереднього випадку.

Катет і прилеглий гострий кут

Нехай відомі катет $b$ і прилеглий до нього кут α.

Гіпотенуза $c$ визначається із співвідношення

$c={\frac {b}{\cos \alpha }}.$

Катет $a$ можна знайти або за теоремою Піфагора аналогічно до попереднього випадку, або із співвідношення

$a=b\ \mathrm {tg} \,\alpha .$

Гострий кут β можна знайти як

$\beta =90^{\circ }-\alpha .$

Катет і протилежний гострий кут

Нехай відомі катет $b$ і протилежний до нього кут β.

Гіпотенузу $c$ можна знайти із співвідношення

$c={\frac {b}{\sin \beta }}.$

Катет $a$ і другий гострий кут α можна знайти аналогічно до попереднього випадку.

Гіпотенуза і гострий кут

Нехай відомі гіпотенуза $c$ і гострий кут β.

Гострий кут α можна знайти як

$\alpha =90^{\circ }-\beta .$

Катети визначаються із співвідношень

$a=c\sin \alpha =c\cos \beta ,$

$b=c\sin \beta =c\cos \alpha .$

Розв'язування сферичних трикутників

Сферичний трикутник загального виду повністю визначається трьома з шести своїх характеристик (3 сторони і 3 кута). Сторони сферичного трикутника $a,b,c$ прийнято вимірювати не лінійними одиницями, а величиною центральних кутів, що спираються на них. Розв'язування трикутників у сферичній геометрії має ряд відмінностей від плоского випадку. Наприклад, сума трьох кутів $\alpha +\beta +\gamma$ залежить від трикутника; крім того, на сфері не існує не рівних подібних трикутників, і тому задача побудови трикутника за трьома кутами має єдиний розв'язок. Але базові співвідношення, що використовуються для розв'язування задачі, аналогічні до плоского випадку: сферичні теореми косинусів і сферична теорема синусів.

Із інших співвідношень можуть бути корисними формули аналогії Непера і формула половини сторони.

Задані три сторони

Три сторони

Якщо сторони $a,b,c$ задані (в кутових одиницях), то кути трикутника визначаються з теореми косинусів:

$\alpha =\arccos \left({\frac {\cos a-\cos b\ \cos c}{\sin b\ \sin c}}\right)$,

$\beta =\arccos \left({\frac {\cos b-\cos c\ \cos a}{\sin c\ \sin a}}\right)$,

$\gamma =\arccos \left({\frac {\cos c-\cos a\ \cos b}{\sin a\ \sin b}}\right)$,

Задані дві сторони і кут між ними

Дві сторони і кут між ними

Нехай задані сторони $a,b$ і кут $\gamma$ між ними. Сторона $c$ знаходиться за теоремою косинусів:

$c=\arccos \left(\cos a\cos b+\sin a\sin b\cos \gamma \right)$

Кути $\alpha ,\beta$ можна знайти так само, як і в попередньому варіанті, можна також використати формули аналогії Непера:

$\alpha =\operatorname {arctg} \ {\frac {2\sin a}{\operatorname {tg} ({\frac {\gamma }{2}})\sin(b+a)+\operatorname {ctg} ({\frac {\gamma }{2}})\sin(b-a)}}$

$\beta =\operatorname {arctg} \ {\frac {2\sin b}{\operatorname {tg} ({\frac {\gamma }{2}})\sin(a+b)+\operatorname {ctg} ({\frac {\gamma }{2}})\sin(a-b)}}$,

Задані дві сторони і кут не між ними

Дві сторони і кут не між ними

Нехай задані сторони $b,c$ і кут $\beta$. Для існування розв'язку необхідним є виконання умов:

$b>\arcsin(\sin c\,\sin \beta )$

Кут $\gamma$ отримується з теореми синусів:

$\gamma =\arcsin \left({\frac {\sin c\,\sin \beta }{\sin b}}\right)$

Тут, аналогічно до плоского випадку, при $b<c$ отримуються два розв'язки: $\gamma$ і $~180^{\circ }-\gamma$.

Інші величини можна знайти з формул аналогії Непера:

$a=2\operatorname {arctg} \left\{\operatorname {tg} \left({\frac {1}{2}}(b-c)\right){\frac {\sin \left({\frac {1}{2}}(\beta +\gamma )\right)}{\sin \left({\frac {1}{2}}(\beta -\gamma )\right)}}\right\}$,

$\alpha =2\operatorname {arcctg} \left\{\operatorname {tg} \left({\frac {1}{2}}(\beta -\gamma )\right){\frac {\sin \left({\frac {1}{2}}(b+c)\right)}{\sin \left({\frac {1}{2}}(b-c)\right)}}\right\}$.

Задані сторона і прилеглі кути

Сторона і прилеглі кути

У цьому варіанті задана сторона $c$ і кути $\alpha ,\beta$. Кут $\gamma$ визначається за теоремою косинусів:

$\gamma =\arccos(\sin \alpha \sin \beta \cos c-\cos \alpha \cos \beta )\,$,

Дві невідомі сторони отримуються з формул аналогії Непера:

$a=\operatorname {arctg} \left\{{\frac {2\sin \alpha }{\operatorname {ctg} (c/2)\sin(\beta +\alpha )+\operatorname {tg} (c/2)\sin(\beta -\alpha )}}\right\}$

$b=\operatorname {arctg} \left\{{\frac {2\sin \beta }{\operatorname {ctg} (c/2)\sin(\alpha +\beta )+\operatorname {tg} (c/2)\sin(\alpha -\beta )}}\right\}$

або, використовуючи обчислений кут $\gamma$, за теоремою косинусів:

$a=\arccos \left({\frac {\cos \alpha +\cos \beta \cos \gamma }{\sin \beta \sin \gamma }}\right)$

$b=\arccos \left({\frac {\cos \beta +\cos \gamma \cos \alpha }{\sin \gamma \sin \alpha }}\right)$

Задані два кути і сторона не між ними

Два кута і сторона не між ними

Нехай задані сторона $a$ і кути $\alpha ,\beta$. Сторона $b$ визначається за теоремою синусів:

$b=\arcsin \left({\frac {\sin a\,\sin \beta }{\sin \alpha }}\right)$,

Якщо кут для сторони $a$ гострий і $\alpha >\beta$, існує другий розв'язок:

$b=\pi -\arcsin \left({\frac {\sin a\,\sin \beta }{\sin \alpha }}\right)$

Інші величини визначаються з формул аналогії Непера:

$c=2\operatorname {arctg} \left\{\operatorname {tg} \left({\frac {1}{2}}(a-b)\right){\frac {\sin \left({\frac {1}{2}}(\alpha +\beta )\right)}{\sin \left({\frac {1}{2}}(\alpha -\beta )\right)}}\right\}$,

$\gamma =2\operatorname {arcctg} \left\{\operatorname {tg} \left({\frac {1}{2}}(\alpha -\beta )\right){\frac {\sin \left({\frac {1}{2}}(a+b)\right)}{\sin \left({\frac {1}{2}}(a-b)\right)}}\right\}$,

Задані три кути

Три кута

Якщо задано три кута, сторони можна знайти за теоремою косинусів:

$a=\arccos \left({\frac {\cos \alpha +\cos \beta \cos \gamma }{\sin \beta \sin \gamma }}\right)$,

$b=\arccos \left({\frac {\cos \beta +\cos \gamma \cos \alpha }{\sin \gamma \sin \alpha }}\right)$,

$c=\arccos \left({\frac {\cos \gamma +\cos \alpha \cos \beta }{\sin \alpha \sin \beta }}\right)$.

Інший варіант: використання формули половини сторони.

Розв'язування прямокутних сферичних трикутників

Викладені алгоритми значно спрощуються, якщо відомо, що один з кутів трикутника (наприклад, кут $C$) прямий. Прямокутний сферичний трикутник повністю визначається двома елементами, інші три знаходяться з допомогою мнемонічного правила Непера або з наведених нижче співвідношень.

$\sin a=\sin c\cdot \sin \alpha =\operatorname {tg} b\cdot \operatorname {ctg} \beta$

$\sin b=\sin c\cdot \sin \beta =\operatorname {tg} a\cdot \operatorname {ctg} \alpha$

$\cos c=\cos a\cdot \cos b=\operatorname {ctg} \alpha \cdot \operatorname {ctg} \beta$

$\operatorname {tg} a=\sin b\cdot \operatorname {tg} \alpha$

$\operatorname {tg} b=\operatorname {tg} c\cdot \cos \alpha$

$\cos \alpha =\cos a\cdot \sin \beta =\operatorname {tg} b\cdot \operatorname {ctg} c$

$\cos \beta =\cos b\cdot \sin \alpha =\operatorname {tg} a\cdot \operatorname {ctg} c$

Варіації та узагальнення

В багатьох практично важливих задачах замість сторін трикутника задаються інші його характеристики — наприклад, довжина медіани, висоти, бісектриси, радіус вписаного чи описаного кола і т. д. Аналогічно замість кутів при вершинах трикутника в задачі можуть фігурувати інші кути. Алгоритми розв'язування подібних задач найчастіше комбінуються із розглянутих вище теорем тригонометрії.

Приклади:

• Задача Реґіомонтана: побудувати трикутник, якщо відомі одна його сторона, довжина опущеної на неї висоти і протилежний кут.
• Задача Снеліуса—Потенота.
• Задача Томаса Фінке: знайти кути трикутника, якщо відома сума двох кутів $\alpha +\beta$ і відношення протилежних сторін $a:b$.
• Задача Ньютона: розв'язати трикутник, якщо відомі одна його сторона, протилежний кут і сума двох інших сторін.

Приклади практичного застосування

Тріангуляція

Визначення відстані з допомогою тріангуляції

Для визначення відстані $d$ від берега до недоступної точки — наприклад, до віддаленого корабля, — потрібно відмітити на березі дві точки, відстань $l$ між якими відома, і виміряти кути $\alpha$ і $\beta$ між лінією, що сполучає ці точки, і напрямком на корабель. З формул варіанту «сторона і прилеглі до неї кути» можна знайти довжину висоти трикутника:

$d={\frac {\sin \alpha \,\sin \beta }{\sin(\alpha +\beta )}}\,l={\frac {\operatorname {tg} \alpha \,\operatorname {tg} \beta }{\operatorname {tg} \alpha +\operatorname {tg} \beta }}\,l$

Цей метод використовується в каботажному судноплавстві. Кути $\alpha ,\beta$ при цьому оцінюються спостереженнями з корабля відомих орієнтирів на землі. Аналогічна схема використовується в астрономії для визначення відстані до близької зорі: вимірюються кути спостереження цієї зорі з протилежних точок земної орбіти (тобто з інтервалом у півроку) і за їх різницею (паралаксом) обчислюють шукану відстань.

Визначення висоти гори

Інший приклад: потрібно виміряти висоту $h$ гори або високої будівлі. Відомі кути $\alpha ,\beta$ спостереження вершини з двох точок, розташованих на відстані $l$. З формул того ж варіанту, що і вище, отримується:

$h={\frac {\sin \alpha \,\sin \beta }{\sin(\beta -\alpha )}}\,l={\frac {\operatorname {tg} \alpha \,\operatorname {tg} \beta }{\operatorname {tg} \beta -\operatorname {tg} \alpha }}\,l$

Відстань між двома точками на поверхні земної кулі

Потрібно обчислити відстань між двома точками на земній кулі:

Точка A: широта $\lambda _{\mathrm {A} },$ довгота $L_{\mathrm {A} },$

Точка B: широта $\lambda _{\mathrm {B} },$ довгота $L_{\mathrm {B} },$

Для сферичного трикутника $ABC$, де $C$ — північний полюс, відомі наступні величини:

$a=90^{\mathrm {o} }-\lambda _{\mathrm {B} }\,$

$b=90^{\mathrm {o} }-\lambda _{\mathrm {A} }\,$

$\gamma =L_{\mathrm {A} }-L_{\mathrm {B} }\,$

Цей випадок «дві сторони і кут між ними». З наведених вище формул отримуємо:

$\mathrm {AB} =R\arccos \left\{\sin \lambda _{\mathrm {A} }\,\sin \lambda _{\mathrm {B} }+\cos \lambda _{\mathrm {A} }\,\cos \lambda _{\mathrm {B} }\,\cos \left(L_{\mathrm {A} }-L_{\mathrm {B} }\right)\right\}$,

де $R$ — радіус Землі.

Історія

Зачатки тригонометричних знань можна знайти в математичних рукописах Стародавнього Єгипту, Вавилону і Стародавнього Китаю. Головним досягненням цього періоду стало співвідношення, яке пізніше отримало назву теореми Піфагора; Ван дер Варден вважає, що вавилоняни відкрили його між 2000 і 1786 роками до н. е.

Загальна постановка задачі розв'язування трикутників (як плоских, так і сферичних) з'явилася в давньогрецькій геометрії. У другій книзі «Начал» Евкліда теорема 12 є словесним аналогом теореми косинусів для тупокутних трикутників:

В тупокутних трикутниках квадрат на стороні, що стягує тупий кут, більший [суми] квадратів на сторонах, що містять тупий кут, на двічі взятий прямокутник, розташований між однією із сторін при тупому куті, на яку падає перпендикуляр, і відрізком при тупому куті, що відтинається цим перпендикуляром ззовні.

Наступна за нею теорема 13 — варіант теореми косинусів для гострокутних трикутників. Аналога теореми синусів у греків не було, це важливе відкриття було зроблене набагато пізніше: найдавніше доведення теореми синусів на площині, із тих, що дійшли до нас, описане в книзі Насир ад-Дін ат-Тусі «Трактат про повний чотиристоронник», написаній в XIII столітті.

Перші тригонометричні таблиці склав, ймовірно, Гіппарх в середині II ст. до н. е. для астрономічних розрахунків. Пізніше астроном II ст Клавдій Птолемей в «Альмагесті» доповнив результати Гіппарха. Перша книга «Альмагеста» — найбільш значима тригонометрична робота всієї античності. Зокрема, «Альмагест» містить докладні тригонометричні таблиці хорд для гострих і тупих кутів, з кроком 30 кутових мінут. В таблицях Птолемей наводить значення довжин хорд з точністю до трьох шістдесяткових знаків. Така точність приблизно відповідає п'ятизначній десятковій таблиці синусів з кроком 15 кутових мінут.

Птолемей явно не формулює теорему синусів і косинусів для трикутників. Однак він завжди справляється із задачею розв'язування трикутників, розбиваючи трикутник на два прямокутних.

Паралельно із розвитком тригонометрії площини греки, під впливом астрономії, далеко розвинули сферичну тригонометрію. Вирішальним етапом у розвитку теорії стала монографія «Сферіка» у трьох книгах, яку написав Менелай Александрійський (близько 100 року н. е.). У першій книзі він виклав теореми про сферичні трикутники, аналогічні до теорем Евкліда про плоскі трикутники (див. I книгу «Начал»). За повідомленням Паппа, Менелай першим ввів поняття сферичного трикутника як фігури, утвореної відрізками великих кругів. Через декілька десятиліть Клавдій Птолемей у своїх працях «Географія», «Аналема» і «Планісферій» дає детальний виклад застосування тригонометрії до картографії, астрономії і механіки.

У IV столітті, після занепаду античної науки, центр розвитку математики перемістився в Індію. Роботи індійських математиків (сідханти) показують, що їхні автори були добре знайомі з працями грецьких астрономів і геометрів. Чистою геометрією індійці цікавилися мало, але їхній внесок у прикладну астрономію і розрахункові аспекти тригонометрії дуже значний. Зокрема, індійці першими ввели у вжиток косинус. Крім того, індійці знали формули для кратних кутів $\sin n\varphi$, $\cos n\varphi$ для $n=2,3,4,5$. В «Сур'я-сідханті» і у працях Брахмагупти при розв'язуванні задач фактично використовується сферичний варіант теореми синусів, однак загальне формулювання цієї теореми в Індії так і не з'явилося.

В VIII століття вчені країн Близького і Середнього Сходу познайомилися з працями давньогрецьких та індійських математиків і астрономів. Їхні астрономічні трактати, аналогічні до індійських сідхантів, називалися Зідж. Типовий зідж був збірником астрономічних і тригонометричних таблиць, разом із посібником по їх використанню і (не завжди) викладом загальної теорії. Порівняння зіджів періоду VIII—XIII століть показує швидку еволюцію тригонометричних знань. Найбільш ранні праці із тих, що збереглися, належать аль-Хорезмі і аль-Марвазі (IX століття), які розглядали, поряд із відомими ще індійцям синусом і косинусом, нові тригонометричні функції: тангенс, котангенс, секанс і косеканс.

Сабіт ібн Курра (IX століття) і аль-Баттані (X століття) першими відкрили фундаментальну теорему синусів для часткового випадку прямокутного сферичного трикутника. Для довільного сферичного трикутника доведення було знайдене (різними способами і, ймовірно, незалежно один від одного) Абу-ль-Вафою, аль-Ходжанді та ібн Іраком наприкінці X століття. В іншому трактаті ібн Ірака сформульована і доведена теорема синусів для плоского трикутника. Сферична теорема косинусів у загальному вигляді сформульована в країнах ісламу не була, однак у працях Сабіта ібн Курри, аль-Баттані та інших астрономів є твердження, які їй еквівалентні.

Фундаментальне викладення тригонометрії як самостійної науки (як плоскої, так і сферичної) дав перський математик і астроном Насир ад-Дін ат-Тусі 1260 року. Його «Трактат про повний чотиристоронник» містить практичні способи розв'язування типових задач, зокрема і найважчих, розв'язаних самим ат-Тусі — наприклад, побудова сторін сферичного трикутника за заданими трьома кутами. Таким чином, до кінця XIII століття були відкриті базові теореми, необхідні для ефективного розв'язування трикутників.

В Європі розвиток тригонометричної теорії став надзвичайно важливим у Новий час, в першу чергу для артилерії, оптики і навігації при дальніх морських подорожах. 1551 року з'явилися 15-значні тригонометричні таблиці Ретика, учня Коперника, з кроком 10". Потреба у складних тригонометричних розрахунках викликала на початку XVII століття відкриття логарифмів, причому перші логарифмічні таблиці Джона Непера містили лише логарифми тригонометричних функцій. Серед інших відкриттів Непера — ефективний алгоритм розв'язування сферичних трикутників, який отримав назву «формул аналогії Непера». Алгебраїзація тригонометрії, почата Франсуа Вієтом, була завершена Леонардом Ейлером у XVIII столітті, після чого алгоритми розв'язування трикутників набули сучасного вигляду.

Див. також

• Подібність трикутників
• Сферична тригонометрія
• Сферичний трикутник
• Сферична теорема Піфагора
• Тріангуляція
• Тригонометричні тотожності
• Тригонометричні функції
• Формули Мольвейде

Література

Теорія і алгоритми

• Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. Геометрия: 7—9 классы. Учебник для общеобразовательных учреждений. — 19-е изд. — М. : Просвещение, 2009. — 384 с. — ISBN 978-5-09-021136-9.(рос.)
• Выгодский М. Я. Справочник по элементарной математике. — М. : Наука, 1978.(рос.)
• Гельфанд И. М., Львовский С. М., Тоом А. Л. Тригонометрия, учебник для 10 класса. — М. : МЦНМО, 2002. — ISBN 5-94057-050-X.(рос.)
• Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М. : Наука, 1976. — 591 с.(рос.)
• Мензел Д. (ред.). Основные формулы физики. Глава 1. Основные математические формулы. — М. : Изд. иностранной литературы, 1957. — 658 с.(рос.)
• Основные понятия сферической геометрии и тригонометрии // Энциклопедия элементарной математики (в 5 томах). — М. : Физматгиз, 1963. — Т. 4. — С. 518-557.(рос.)
• Степанов Н. Н. Сферическая тригонометрия. — М.—Л. : ОГИЗ, 1948.(рос.)

Історія

• Глейзер Г. И. История математики в школе. VII-VIII классы. Пособие для учителей. — М. : Просвещение, 1982. — С. 76-95.(рос.)
• Глейзер Г. И. История математики в школе. IX-X классы. Пособие для учителей. — М. : Просвещение, 1983. — 352 с.(рос.)
• История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука.
  • История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М. : Наука, 1970. — Т. I.(рос.)
  • Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М. : Наука, 1970. — Т. II.(рос.)
  • Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М. : Наука, 1972. — Т. III.(рос.)
• Матвиевская Г. П. Очерки истории тригонометрии: Древняя Греция. Средневековый Восток. Позднее Средневековье. — Изд. 2-е. — М. : Либроком, 2012. — 160 с. — (Физико-математическое наследие: математика (история математики)) — ISBN 978-5-397-02777-9.(рос.)
• Рыбников К. А. История математики в двух томах. — М. : Изд. МГУ, 1960. — Т. I.(рос.)
• Сираждинов С. Х., Матвиевская Г. П. Абу Райхан Беруни и его математические труды. Пособие для учащихся. — М. : Просвещение, 1978. — 95 с. — (Люди науки)(рос.)
• Цейтен Г. Г. История математики в древности и в средние века. — М.-Л. : ГТТИ, 1932. — 230 с.(рос.)
• Цейтен Г. Г. История математики в XVI и XVII веках. — М.-Л. : ОНТИ, 1938. — 456 с.(рос.)