Оптичний пінцет

Опти́чний пінце́т (англ. Laser tweezers), інколи «опти́чні щи́пці», «ла́зерні щи́пці» або «опти́чна па́стка» — науковий прилад, що дозволяє маніпулювати мікроскопічними об'єктами за допомогою лазерного світла (зазвичай лазерного діода). Дозволяють прикладати до діелектричних об'єктів сили, величиною від фемтоньютонів до наноньютонів і вимірювати відстані від кількох нанометрів до мікрометрів. В останні роки оптичний пінцет став популярним знаряддям у біофізиці, де його використовують при дослідженні структури та принципу роботи білків.

2018 року творцям оптичного пінцета присуджено Нобелівську премію з фізики «за винайдення оптичного пінцета та його застосування в біологічних системах».

Історія

Ще в XVII столітті висловлювалися припущення, що світло може чинити тиск на речовину. В роботі «De Cometis» німецький астроном Кеплер висунув думку, що хвости комет відхиляються під дією сонячного світла. Хоча пізніше виявилося, що це не єдиний механізм такого відхилення, ідея Кеплера стала важливою для розвитку астрономії. Наприклад, дослідження показали, що світловий (радіаційний) тиск — один з найголовніших механізмів, які відповідають за динаміку частинок в міжзоряному просторі. Через два сторіччя Максвелл за допомогою своєї теорії електромагнітних явищ розрахував величину світлового тиску. Експериментальні дослідження, які 1900 року провів російський фізик Лебедєв, підтвердили існування тиску світла.

Після відкриття Басовим та Прохоровим у 1953 році принципу дії лазера, з'явилося джерело світла, достатньо потужне та з пучком світла, достатньо колімованим для маніпулювання макроскопічними об'єктами. Але тільки 1970 року в науковій літературі з'явилися публікації співробітника Bell Labs Артура Ешкіна, в яких повідомлялося про реєстрацію оптичних сил розсіяння і градієнтних сил на частинках мікронних розмірів. Через кілька років Ешкін із колегами повідомили про перше спостереження того, що зараз називають оптичною пасткою, тобто пучка світла, сфокусованого так, що він може стійко утримувати мікроскопічні частинки (10 нм—10 мкм) у трьох вимірах.

Подібний принцип використовують і для лазерного охолодження, методу зниження температури атомів у оптичній пастці до значень, недосяжних іншими засобами, запропонований 1968 року радянським фізиком Летоховим і реалізований 1978 року тією ж групою Ешкіна. Колишній співробітник Ешкіна Стівен Чу продовжив дослідження і 1997 року отримав за цю роботу Нобелівську премію.

У 1980-х роках Стівен Блок і Говард Берг уперше застосували технологію оптичного пінцета в біології для того, щоб утримати бактерію з метою дослідження бактеріальних джгутиків. Вже в 1990-х роках дослідники Карлос Бустаманте, Джеймс Спудіч і Стівен Блок застосували метод оптичної силової спектроскопії для дослідження біологічних двигунів молекулярного масштабу. Ці молекулярні двигуни всюдисущі в природі і відповідають за переміщення та механічні дії в клітині. Оптичні пастки дозволили цим біофізикам спостерігати динаміку молекулярних двигунів, розглядаючи одну вибрану молекулу окремо від інших. Оптична силова спектроскопія дозволила краще зрозуміти природу рушійних сил, які діють у молекулі й мають стохастичну (випадкову) природу.

Оптичний пінцет виявився корисними і в інших галузях біології. Наприклад, 2003 року метод оптичного утримання використано для сортування клітин. Створюючи в ділянці, наповненій мікробіологічним зразком, світлову картину великої інтенсивності, можна сортувати клітини за їхніми власними оптичними характеристиками. Оптичний пінцет також використано для дослідження цитоскелета, вимірювання в'язкоеластичних властивостей біополімерів та вивчення рухливості клітин.

2018 року Артур Ешкін, Жерар Муру і Донна Стрікленд отримали нобелівську премію за розробку і застосування оптичного пінцета.

Фізичні принципи

Загальний огляд

Маленькі діелектричні сфери взаємодіють з електричним полем, створеним світловою хвилею, завдяки наведеному дипольному моменту. В результаті взаємодії цього диполя з полем, сфера втягується уздовж градієнту електричного поля до точки найвищої інтенсивності світла. Крім градієнтної сили, на сферу також діє розсіювальна сила, викликана відбиттям світла від її поверхні. Ця сила штовхає сферу вздовж пучка світла. Проте, якщо промінь сильно сфокусований, градієнт інтенсивності долає силу світлового тиску.

Детальніший аналіз, проведений Ешкіном, базується на двох механізмах, дія яких залежить від розміру частинки. З теорії розсіювання відомо, що частинка в повітрі, залежно від свого розміру, розсіює світло по-різному. Якщо розмір розсівних частинок набагато менший, ніж довжина хвилі світла, це розсіювання називають релеївським (від імені британського фізика лорда Релея). Релеївське розсіювання зростає із збільшенням частоти електромагнітної хвилі, тому при розсіюванні білого світла розсіяне світло матиме блакитний відтінок. Відповідно світло, яке проходить прямо має червоний відтінок. Цей ефект спричиняє червоні барви заходу сонця і блакитний колір неба. Коли світло розсіюється на частинках (пил, дим, водяні крапельки), розмір яких більший, ніж довжина хвилі світла, закони розсіювання складніші. В загальному випадку задачу про розсіювання світла сферою, незалежно від розмірів сфери, розв'язав німецький фізик Густав Мі. Розсіюванням Мі пояснюють білизну хмар.

Використовуючи ці ідеї, Ешкін запропонував аналізувати оптичне мікроманіпулювання двома окремими методами, а саме, підходом фізичної оптики для великих частинок (діаметр частинки d > λ, де λ — довжина хвилі світла) і наближенням електричного диполя для релеївських частинок (d < λ).

Фізична оптика

Пояснення на основі фізичної оптики. Коли кулька зміщується від центра пучка, як на малюнку (a), найбільша зміна імпульсу променів з більшою інтенсивністю викликає появу сили, спрямованої до центра пастки. Коли кулька розташована в центрі пучка, як показано на малюнку (b), сила напрямлена в бік звуження

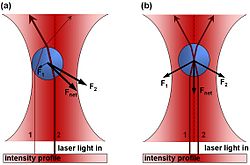
Підхід хвильової оптики до процесів заломлення і відбиття світла від мікросфери дозволяє проаналізувати втягування в оптичну пастку (див. малюнок).

Найпростіше зрозуміти сили, які діють на мікроскопічну частинку з боку сфокусованого променя, можна використовуючи принципи геометричної оптики. Попадаючи на частинку промінь відбивається і заломлюється. При цьому змінюється напрям його руху, а отже й імпульс фотонів. За законом збереження імпульсу, зміна імпульсу передається частинці.

Використовуючи просту діаграму променів і розглядаючи напрямки імпульсів відбитих і заломлених променів, можна помітити, що на мікросферу діють дві різні оптичні сили. Як видно з діаграми, результуюча сила тягне сферу в напрямку області найвищої інтенсивності променя. Цю силу називають градієнтною. Крім того, на сферу діє світловий тиск, штовхаючи її в напрямку падіння променя.

У своєму першому експерименті Ешкін використав міліватний гаусівський пучок одномодового (TEM₀₀) аргонового лазера з довжиною хвилі 514,5 нм, сфокусованого в пляму діаметром w₀ = 6,2 мкм. Він рухав за допомогою цього пучка латексні кулі діаметром 0,51; 1,31 і 2,68 мкм у воді й повітрі. Для куль радіусом r = 1,31 мкм, поміщених у воду, за потужності лазера P = 19 мВт швидкість куль досягала 26 мкм/с. А з оцінки за формулою

$v={\frac {2qPr}{3\pi cw_{0}^{2}\eta }},$

де q — частка світла, ефективно відбитого від сфери (0,062), c — швидкість світла, η — динамічна в'язкість рідини (1 мПа·с для води) виходить 29 мкм/с. А відповідна сила, що діє на частинку, виходить із закону Стокса

$F=6\pi r\eta v$

і становить 730 фН.

У повітрі найбільша швидкість крапель води діаметром 5 мкм за потужності лазера 50 мВт склала 0,25 см/c.

Щоб досліджуваний об'єкт залишався нерухомим, необхідно скомпенсувати силу, зумовлену тиском світла. Це можна зробити, використовуючи два зустрічні пучки світла, які штовхатимуть кулю в протилежних напрямках, або за допомогою сильно сфокусованого гаусівського пучка (з високою числовою апертурою, NA>1.0). В цьому випадку світловий тиск компенсується високою градієнтною силою.

Схема експерименту з вимірювання сил, які діють на РНК-полімеразу, що рухається уздовж ДНК.

З іншого боку, в релеївському режимі, форма частинок несуттєва. Взагалі, для найменших частинок потрібна найменша сила притягання. В більшості випадків, для пояснення робочого механізму оптичного пінцета для будь-якої форми частинок застосовують модель наведеного диполя. Електромагнітна хвиля індукує диполь, або поляризацію, в діалектичній частинці. Сила взаємодії цього диполя зі світлом спричиняє виникнення градієнтної сили притягання.

Детальніше про прилад із оптичною пасткою в лабораторії Стівена Блока можна дізнатися на сайті Стенфордського університету.

Наближення електричного диполя

У випадках, коли діаметр спійманої в пастку частинки значно менший, ніж довжина хвилі світла, умови задовольняють умову розсіювання Релея, і частинку можна розглянути як точковий диполь у неоднорідному електромагнітному полі. Сила, що діє на заряджену частинку в електромагнітній області, відома як сила Лоренца:

$\mathbf {F} _{1}=q\left(\mathbf {E} _{1}+{\frac {d\mathbf {x} _{1}}{dt}}\times \mathbf {B} \right).$

Сила, що діє на диполь, обчислюється за сумою сил, що діють на окремі заряди.: $\mathbf {F} =\mathbf {F} _{1}+\mathbf {F} _{2}$,

$\mathbf {F} =q\left(\mathbf {E} _{1}(x,y,z)-\mathbf {E} _{2}(x,y,z)+{\frac {d(\mathbf {x} _{1}-\mathbf {x} _{2})}{dt}}\times \mathbf {B} \right).$

Через невелику відстань $\mathbf {d} =\mathbf {x} _{1}-\mathbf {x} _{2}$ між зарядами в диполі можна розкласти напруженість електричного поля поблизу першого заряду:

$\mathbf {F} =q\left(\mathbf {E} _{1}(x,y,z)+(\mathbf {d} \cdot \nabla )\mathbf {E} -\mathbf {E} _{1}(x,y,z)+{\frac {d\mathbf {d} }{dt}}\times \mathbf {B} \right).$

Зауважте, що $\mathbf {E} _{1}$ скорочується. Розкриваючи дужки та замінюючи добуток заряду $q$ на відстань $\mathbf {d}$ поляризацією диполя $\mathbf {p} =q\mathbf {d}$, маємо

$\mathbf {F} =(\mathbf {p} \cdot \nabla )\mathbf {E} +{\frac {d\mathbf {p} }{dt}}\times \mathbf {B} =\alpha \left[(\mathbf {E} \cdot \nabla )\mathbf {E} +{\frac {d\mathbf {E} }{dt}}\times \mathbf {B} \right],$

де у другій рівності припущено, що поляризація частинки є лінійною функцією напруженості електричного поля (тобто $\mathbf {p} =\alpha \mathbf {E}$).

Якщо тепер скористатися рівнянням із векторного аналізу

$(\mathbf {E} \cdot \nabla )\mathbf {E} =\nabla \left({\frac {1}{2}}E^{2}\right)-\mathbf {E} \times (\nabla \times \mathbf {E} )$

і одним із рівнянь Максвелла,

$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}},$

отримаємо

$\mathbf {F} =\alpha \left[{\frac {1}{2}}\nabla E^{2}+{\frac {d}{dt}}(\mathbf {E} \times \mathbf {B} )\right].$

Другий доданок в останній рівності — похідна за часом величини, яка пов'язана через сталий множник із вектором Пойнтінга, який описує потужність випромінювання, що проходить через одиничну площу. Припускаючи, що потужність лазера не залежить від часу, похідна цього доданку — нуль, і сила запишеться як

$\mathbf {F} ={\frac {1}{2}}\alpha \nabla E^{2}.$

Квадрат величини напруженості електричного поля дорівнює інтенсивності променя як функції координат. Тому результат вказує, що сила, яка діє на діелектричну частинку, в наближенні точкового диполя, пропорційна градієнту інтенсивності пучка. Інакше кажучи, описана тут сила приводить до тяжіння частинки в область з найвищою інтенсивністю. Насправді сила, що виникає при розсіюванні світла залежить лінійно від інтенсивності променя, поперечного перерізу частинки і показника заломлення середовища, в якому міститься пастка (наприклад, вода), діє проти градієнтної сили в напрямі осі пастки, приводячи до деякого зміщення вниз від положення максимуму інтенсивності.

Наближення гармонічного потенціалу

Корисний спосіб вивчити взаємодію атома з пучком Гаусса — наближення гармонійного потенціалу профілю інтенсивності, який діє на атом. У випадку дворівневого атома цей потенціал пов'язаний із його зсувом Аутлера — Таунса,

$\mathbf {\Delta E} _{\text{AC Stark}}={\frac {3\pi c^{2}\Gamma \mu }{2\omega _{0}^{3}\delta }}\mathbf {I(r,z)}$

де $\Gamma$ — природна ширина лінії збудженого стану, $\mu$ — електричний дипольний зв'язок, $\omega _{o}$ — частота переходу, $\delta$ — розладування або різниця між частотою лазера та частотою переходу.

Інтенсивність профілю гаусового променя характеризується довжиною хвилі $(\lambda )$, найменшим звуженням $(w_{o})$ і потужністю променя $(P_{o})$. Профіль променя визначають такі формули:

$I(r,z)=I_{0}\left({\frac {w_{0}}{w(z)}}\right)^{2}e^{-{\frac {2r^{2}}{w^{2}(z)}}}$

$w(z)=w_{0}{\sqrt {1+\left({\frac {z}{z_{R}}}\right)^{2}}}$

$z_{R}={\frac {\pi w_{0}^{2}}{\lambda }}$

$P_{0}={\frac {1}{2}}\pi I_{0}w_{0}^{2}$

Щоб апроксимувати цей гаусівський потенціал як у радіальному, так і в осьовому напрямках променя, профіль інтенсивності слід розширити до другого порядку за $z$ і $r$ для $r=0$ і $z=0$ відповідно і прирівняти до гармонічного потенціалу ${\frac {1}{2}}m(\omega _{z}^{2}z^{2}+\omega _{r}^{2}r^{2})$. Ці розширення оцінюються за умови фіксованої потужності.

${\frac {1}{2!}}{\frac {\partial ^{2}I}{\partial z^{2}}}{\Biggr |}_{r,z=0}z^{2}={\frac {2P_{0}\lambda ^{2}}{\pi ^{3}w_{0}^{6}}}z^{2}={\frac {1}{2}}m\omega _{z}^{2}z^{2}$

${\frac {1}{2!}}{\frac {\partial ^{2}I}{\partial r^{2}}}{\Biggr |}_{r,z=0}r^{2}={\frac {4P_{0}}{\pi w_{0}^{4}}}r^{2}={\frac {1}{2}}m\omega _{r}^{2}r^{2}$

Це означає, що при розв'язанні для гармонійних частот (або частот пасток, коли розглядаються оптичні пастки для атомів), частоти подано як:

$\omega _{r}={\sqrt {\frac {8P_{0}}{\pi mw_{0}^{4}}}}$

$\omega _{z}={\sqrt {\frac {4P_{0}\lambda ^{2}}{m\pi ^{3}w_{0}^{6}}}}$

так що відносні частоти захоплення для радіального та осьового напрямків як функція лише звуження променя, як:

${\frac {\omega _{r}}{\omega _{z}}}={\sqrt {2}}{\frac {w_{0}\pi }{\lambda }}$

Оптична левітація

Щоб підняти частинку в повітрі, спрямованій вниз силі тяжіння мають протидіяти сили, що виникають від передання імпульсу фотона. Як правило, тиск фотонного випромінювання сфокусованого лазерного променя достатньої інтенсивності протидіє спрямованій вниз силі тяжіння, а також запобігає латеральній (з боку в бік) і вертикальній нестабільності, створюючи стабільну оптичну пастку, здатну утримувати дрібні частинки в завислому стані.

У цьому типі експерименту використовуються прозорі діелектричні мікросфери (діаметром від кількох до 50 мкм), такі як кульки з плавленого кремнезему, краплі олії чи води. Довжина хвилі лазерного випромінювання може бути фіксованою, як у аргонового іонного лазера або регульованого лазера на барвнику. Необхідна потужність лазера становить близько 1 Вт, сфокусована в пляму розміром кілька десятків мікрометрів. Явища, пов'язані з морфологічно залежними резонансами в сферичній оптичному резонаторі, вивчали кілька дослідницьких груп.

Для блискучого об'єкта, такого як металева мікросфера, стабільної оптичної левітації не досягнуто. Оптична левітація макроскопічного об'єкта також теоретично можлива і може бути посилена за допомогою наноструктурування.

Успішно піднято такі матеріали, як чорний луг, оксид алюмінію, вольфрам і нікель.

Будова оптичного пінцета

Оптичний пінцет на альтернативних лазерних модах

Перший оптичний пінцет працював на одному гаусівському пучку (фундаментальна лазерна мода TEM₀₀). 1986 року А. Ешкін розвинув концепцію однопучкового оптичного пінцета, що діють за рахунок використання лазерних мод високого порядку, тобто ермітівських гаусівських пучків (TEM_xy), лагерівських гаусівських пучків (Lg, TEM_pl) і бесселівських пучків (Jn).

Оптичний пінцет на лагерівських гаусівських пучках має унікальну можливість втягування в пастку частинок з високим оптичним відбиттям і поглинанням. Лагерівські гаусівські пучки також мають власний кутовий момент, який уможливлює обертання частинок. Цей ефект спостерігається без зовнішнього механічного або електричного регулювання променя. Передаючи світло з коловою поляризацією і використовуючи хвильову пластинку, можна надати гаусівському пучку спінового орбітального моменту.

Окрім лагерівських гаусівських пучків, бесселівські пучки як нульового, так і вищих порядків, мають орбітальний момент, а також унікальну властивість утримувати одночасно багато частинок на деякій відстані одна від іншої.

Орбітальний момент пучків високого порядку також дозволяє їм керувати штучними наномашинами.

Мультиплексний оптичний пінцет

Типова установка використовує тільки один або два лазерних промені. Складніші експерименти вимагають одночасної роботи багатьох пасток. Цього можна добитися, використовуючи єдиний лазер, світло якого проходить через акустико-оптичний модулятор або через електронно керовані дзеркала. Ці пристрої дозволяють розбити лазерне випромінювання на кілька розділених у часі променів. За допомогою дифракційних оптичних елементів досягають розбиття на кілька променів розділених просторово.

Оптичний пінцет, заснований на оптичних волокнах

Optical Cell Rotator — волоконна лазерна пастка, в якій можна утримувати та точно орієнтувати живі клітини для томографічної мікроскопії

У пристрої цього типу лазерне випромінювання подається через оптичне волокно. Якщо один кінець оптичного волокна має опуклу поверхню, то така форма дозволить сфокусувати світло так, щоб утворити оптичну пастку з високою числовою апертурою.

Якщо ж кінці волокна не опуклі, лазерне світло розходитиметься, і тому стійку оптичну пастку можна утворити тільки при розміщенні двох кінців волокон з різних боків від оптичної пастки, добиваючись балансу градієнтних сил і сил світлового тиску. Градієнтні сили утримують частинки в поперечному напрямі, тоді як поздовжні сили, зумовлені оптичним тиском двох зустрічних променів компенсуватимуть одна одну. Рівноважна z-позиція кулі в такий пастці — таке положення, де дві сили світлового тиску рівні між собою. Такий оптичний пінцет вперше розробили А. Констебль і Дж. Глюк, які використовували цю методику для розтягнення мікрочастинок. Маніпулюючи вхідною потужністю з обох кінців волокна, можна регулювати розтягувальну силу. Така система може використовуватися для вимірювання в'язкоеластичних властивостей клітин. Її чутливість достатня, щоб розрізнити фенотипи цитоскелету. Недавні експерименти продемонстрували можливість диференціації ракових клітин від нормальних.

Оптичний пінцет у сортуванні клітин

Одна з найпоширеніших систем сортування клітин використовує метод проточної цитометрії та флюоресцентну візуалізацію. У цьому методі суспензія біологічних клітин сортується в кілька контейнерів за флюоресцентними характеристиками кожної клітини в потоці. Процесом сортування керує електростатична відхильна система, яка скеровує клітину до певного контейнера зміною напруженості прикладеного електричного поля.

В оптично керованій системі сортування, клітини пропускають через дво- або тривимірні оптичні ґратки. Без поляризації електричним полем клітини сортуються в залежності від того, як вони заломлюють світло. Для створення таких оптичних ґраток група Кішана Долакіа розробила методику використання дифракційної оптики й інших оптичних елементів. З іншого боку, група в Університеті Торонто побудувала сортувальну систему, використовуючи просторовий модулятор світла.

Головний механізм сортування — розташування вузлів оптичної ґратки. Коли потік клітин проходить через оптичну ґратку, на них діють сили тертя і градієнтні сили від найближчих вузлів оптичної ґратки. Змінюючи розташування вузлів, можна створити оптичну доріжку, якою будуть рухатися клітини. Але така доріжка буде ефективною тільки для клітин з певним показником заломлення. Лише вони будуть ефективно відхилятися нерівномірним світловим потоком. Регулюючи швидкість потоку клітин і потужність світла можна отримати хороше оптичне сортування клітин.

Для високої ефективності оптичного сортування баланс сил у системі сортування потребує точного юстування. Зараз^[коли?] в Університеті Сент-Ендрюса (Велика Британія) створено велику дослідницьку групу для роботи над цією проблемою. У випадку успіху ця технологія зможе замінити традиційне флюоресцентне сортування клітин.

Оптичний пінцет на еванесцентних полях

Еванесцентне поле — електромагнітне поле, що проникає вглиб поверхні, наприклад, під час повного внутрішнього відбиття. Це світлове поле згасає за експоненційним законом, проникаючи в матеріал менш ніж на довжину хвилі. Еванесцентне поле знайшло низку застосувань у оптичній мікроскопії нанометрових об'єктів, оптична мікроманіпуляція (оптичний пінцет) стає ще одним його застосуванням.

В оптичному пінцеті неперервне еванесцентне поле може бути створене, коли світло поширюється через оптичний хвилевід (багаторазове повне внутрішнє відбиття). Отримане еванесцентне поле має напрямлений імпульс, і рухатиме мікрочастинки вздовж напрямку свого поширення. Цей ефект відкрили 1992 року С. Кавата і Т. Сугіура. Вони показали, що поле може зв'язувати частинки в тонкому шарі товщиною близько 100 нм. Це пряме зв'язування поля розглядається як тунелювання фотонів до частинок через проміжок між світловідбивним середовищем і оптичною призмою. В результаті виникає напрямлена оптична сила.

Недавня версія оптичного пінцета на еванесцентному полі використовує широку оптичну поверхню, що дозволяє одночасно скеровувати в бажаному напрямі багато частинок, не використовуючи хвилеводу. Цю методику названо безлінзовим оптичним утриманням (англ. Lensless optical trapping, LOT). Точно напрямленого руху частинок досягають завдяки лінуванню Рончі, яке створює в скляній пластинці чіткі оптичні потенціальні ями. Зараз вчені також працюють над фокусуванням еванесцентних полів.

Непрямий підхід до оптичного пінцета

Ще один варіант маніпулювання мікрочастинками за допомогою світла розробив Мінг Ву (Ming Wu), професор радіотехніки в Берклі. Його система не використовує світлового імпульсу безпосередньо. Натомість частинки, якими потрібно маніпулювати, розташовують неподалік від скляної пластинки, вкритої фотоелектричною речовиною. На цю пластинку подають невелику напругу з метою створення на частинках електростатичного заряду. Фотоелектрична пластинка освітлюється світлодіодами, потужність яких можна модулювати, проєктуючи на поверхню будь-яке динамічне зображення. Під дією світла фотоелектрична поверхня заряджається і починає притягати або відштовхувати частинки. Маніпуляцію виконують за допомогою зміни електричного поля, що вмикається за допомогою спроектованого зображення.

Одне із застосувань цього методу — сортування живих та мертвих клітин. Воно ґрунтується на тому, що живі клітини наповнені електролітом, а мертві — ні, тому живі та мертві клітини можна легко розділити. Збудована професором Ву система дозволяє одночасно маніпулювати приблизно 10 тисячами клітин або частинок.

Оптичне зв'язування

Коли група мікрочастинок утримається монохроматичним лазерним пучком, розташування мікрочастинок у межах оптичної пастки залежить від перерозподілу сил взаємодії між частинками через наведені дипольні моменти. Можна сказати, що кластер мікрочастинок і світло в його межах зв'язані в одне ціле. Перші свідчення про існування оптичного зв'язування повідомила лабораторія Джене Головченка в Гарвардському університеті.

Вимірювання оптичних сил

Нині силу притягання мікрочастинок світлом можна виміряти як на одно- так і на двопучковому оптичному пінцеті (фотонний силовий мікроскоп). Недавно^[коли?] розпочато роботи з вимірювання оптичних сил у голографічному оптичному пінцеті з метою досягнення високої точності експерименту.

Основний принцип вимірювання оптичної сили оптичного пінцета — передача імпульсу світла, пов'язана із заломленням світла на частинках. Зміна напрямку поширення світла як у поперечному, так і в поздовжньому напрямках забезпечує силу, що діє на об'єкт. Тому найменшу поперечну силу можна виміряти за відхиленням пучка, який пройшов крізь частинку. Таке відхилення легко вимірюється за допомогою детектора осьової позиції. Найпростіший такий детектор — квадрантний фотодіод — пластинка, поділена на чотири сектори, з пучком світла сфокусованим у її центрі. Якщо мікрочастинка розташована в центрі оптичної пастки, на сектори фотодіода падає світло однакової інтенсивності і різниця сигналів зі секторів дорівнює 0. Але, якщо на частинку діє зовнішня сила, вона зміщується з положення рівноваги в напрямку дії сили, змінюючи при цьому розподіл інтенсивності на фотодіоді. Відповідно, різниця сигналів зі секторів стане ненульовою і буде пропорційна зовнішній силі.

Такий принцип застосовний до будь-якого оптичного пінцета. Найбільшою проблемою при таких вимірюваннях є шум, спричинений броунівським рухом. Однак, цим методом можна вимірювати сили порядку піконьютона та зсув порядку нанометра.

Дослідницькі групи

• ATOM3D [Архівовано 17 квітня 2006 у Wayback Machine.] об'єднана дослідницька група 7 європейських оптичних лабораторій, які працюють із оптичним пінцетом, підтримувана EC Sixth Framework Programme (FP6).
• Лабораторія Блока [Архівовано 23 квітня 2006 у Wayback Machine.], Стенфордський університет, США
• Лабораторія Бустаманте, Університет Каліфорнії, Берклі, США
• Лабораторія Дюфресне [Архівовано 15 липня 2006 у Wayback Machine.], Єльський університет, США
• Лабораторія Фюрста [Архівовано 11 травня 2006 у Wayback Machine.], Делаверський університет, США
• Лабораторія Грієра [Архівовано 14 червня 2006 у Wayback Machine.], Нью-Йоркський університет, США
• Лабораторія Гросса, Університет Каліфорнії, Ірвайн, США
• Лабораторія Ленга [Архівовано 9 серпня 2006 у Wayback Machine.], MIT, США
• Лабораторія Майнерса [Архівовано 7 травня 2011 у Wayback Machine.], Університет Мічигану, США
• Лабораторія Оддершеде, Інститут Нільса Бора, Копенгагенський університет, Данія
• Optical trapping Group [Архівовано 5 жовтня 2002 у Wayback Machine.], Університет Сент-Ендрюса, Шотландія, Велика Британія
• Optical Tweezers Group [Архівовано 7 жовтня 2007 у Wayback Machine.], ICFO
• Optical Tweezers, Університет міста Умео, Швеція
• UQ Optical Micromanipulation Group [Архівовано 4 березня 2016 у Wayback Machine.], Університет Квінсленду, Австралія
• Optics tweezing, Університет Глазго, Шотландія
• Група OMITEC [Архівовано 16 липня 2006 у Wayback Machine.], Інститут наукових приладів, Чехія
• Лабораторія Перкінса, Університет Колорадо, Боулдер, США
• Лабораторія Ванга [Архівовано 8 вересня 2010 у Wayback Machine.], Корнелльський університет, США
• Лабораторія Вуйте [Архівовано 15 травня 2006 у Wayback Machine.], Амстердамський вільний університет, Нідерланди

Див. також

• Пінцет — інформація про механічний прилад, від якого оптичний пінцет отримав свою назву

Посилання

Професійні огляди оптичних пінцетів

• A. Ashkin, «Optical trapping and manipulation of neutral particles using lasers»[1] [Архівовано 11 липня 2006 у Wayback Machine.]
• Neuman, K.C., and Block S.M Review on Optical Trapping method [2] [Архівовано 7 березня 2007 у Wayback Machine.]
• M. Lang and S. Block, A Resource Letter on Optical Tweezers [3] [Архівовано 7 березня 2007 у Wayback Machine.]
• K.Dholakia on Recent review of state of the art tweezers [4]
• D. McGloin on Review of Bessel beam optical tweezers [5]
• David Grier on A revolution in optical manipulation [6] [Архівовано 2 вересня 2006 у Wayback Machine.]
• Спеціальне видання журналу Journal of Modern Optics. Підбірка праць щодо оптичного пінцета кількох провідних груп [7]
• Детальніший список посилань наведено в рукописі Джастіна Моллоя (Justin E Molloy) [8] та Майлза Паджетта (Miles J Padgett) [9] , опублікованому онлайн під назвою Lights, Action: Optical Tweezers[10].

Ресурси інтернету

• Що таке оптичний пінцет [11] (англ.)
• Останні праці, пов'язані з оптичним пінцетом [12] (англ.)
• BBC Frontier розказує про методику оптичного пінцета (2003) [13] [Архівовано 20 лютого 2006 у Wayback Machine.] (англ.)
• Фільми, що показують позиціювання та обертання, керовані оптичним пінцетом [14]
• Фільми про використання оптичного пінцета для роботи з бактеріями [15] [Архівовано 5 листопада 2015 у Wayback Machine.]
• Блог про оптичний пінцет [16] [Архівовано 8 липня 2011 у Wayback Machine.] (англ.)
• Посилання на сторінки лабораторій всесвітнього товариства дослідників оптичних пінцетів на сайті університету Сент-Ендрюса, Шотландія. [17] [Архівовано 3 травня 2006 у Wayback Machine.]

Комерційні системи оптичних пінцетів

• Arryx [Архівовано 6 грудня 2005 у Wayback Machine.]
• Cell Robotics [Архівовано 11 липня 2007 у Wayback Machine.]
• Elliot Scientific [Архівовано 5 липня 2007 у Wayback Machine.]
• MMI Molecular Machines & Industries [Архівовано 11 липня 2007 у Wayback Machine.]
• PALM