Тунелювання
| Квантова механіка |
|---|
|
Вступ · Історія Математичні основи[en] |
|
Фундаментальні поняття |
|
Наближені методи |
|
Відомі науковці |
Тунелюва́ння або тунельний ефект — фізичне явище, яке полягає в тому, що фізичний об'єкт долає потенційний бар'єр, величина якого більша від його кінетичної енергії. Найвідомішим прикладом явища є альфа-розпад. Це явище існує завдяки хвильовій природі квантових процесів, але проявляється не лише у квантових системах. Приклади тунелювання можна спостерігання і в оптиці, де процеси також описуються хвильовими рівняннями.
Термоядерний синтез можливий лише тоді, коли ядра атомів дейтерію долають кулонівський бар'єр завдяки тунелюванню крізь нього.
Важливими застосуваннями явища тунелювання є резонансний тунельний діод та тунельний мікроскоп, тунелювання використовується для розрядки елементів флеш-пам'яті. Тунелювання світла використовується у методі неповного внутрішнього відбиття та приладах, робота яких базується на ньому.
Історія[ред. | ред. код]
Вперше, ефект, аналогічний тунельному, був відкритий у оптиці — що не дивно, адже у фотонів хвильові властивості проявляються найбільш яскраво. Під час повного внутрішнього відбиття, світло проникає у речовину на невелику глибину (еванесцентна хвиля), експоненційно затухаючи з глибиною.[1]
У 1901 році, Роберт Френсіс Ерхарт, досліджуючи провідність газів між двома близько розташованими електродами (використовуючи інтерферометр Майкельсона для вимірівання відстані між ними), відкрив відхилення від закону Пашена, що існує на таких відстанях. У 1926, Франц Ротер, повторюючи дослід Ерхарта з більш чутливим гальванометром зміг виміряти рівень вакуумної емісії електронів.[2]
У 1927 році Фрідріх Гунд описав тунельний ефект, обчислюючи основний квантовий стан частинки у w-подібному потенціалі.[3] У 1928 Георгій Гамов, і, незалежно від нього, Рональд Герні і Едвард Кондон використали теорію тунелювання для створення математичної моделі альфа-розпаду.[4] Ця модель дозволила пов'язати період напіврозпаду ядра і енергію частинок, що вилітають.
Відвідавши семінар Гамова, Макс Борн зрозумів загальність явища тунелювання. Він показав, що цей ефект стосується не лише ядерної фізики, але є універсальним результатом квантової механіки, що стосується великої кількості різноманітних систем. Відкриття напівпровідників, а також винаходження транзисторів і діодів призвело до розуміння принципів тунелювання електронів у твердих тілах. Роботи Лео Есакі, Айвара Джайєвера і Браяна Джозефсона передбачили тунелювання куперівських пар у надпровідниках, за що вони отримали нобелівську премію у 1973 році.
Вступ[ред. | ред. код]
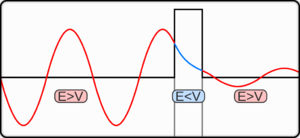
У класичній механіці, задача про проходження частинкою потенціального бар'єру є простою і однозначною: якщо кінетична енергія частинки менша за висоту бар'єру, то частинка ніколи не проходить бар'єр, а якщо навпаки — то завжди проходить. Проте, у квантовій теорії від математичної абстракції матеріальної точки довелося відмовитися, через те, що будь-яка частинка має хвильові властивості. В квантовій механіці частинки описуються хвильовими функціями, квадрат модуля яких задає густину ймовірності перебування частники в певній точці простору. Просторові розміри цих хвиль не є нехтуваними — наприклад, електрону з енергією 1 кЕв відповідає довжина хвилі майже в 10 разів більша за борівський радіус. [1] При товщині бар'єру, порівняному з довжиною хвилі, частинка має шанс пройти через бар'єр. Це явище називається тунелюванням, через те, що частинка не витрачає енергії при цьому — її кінетична енергія на виході з бар'єру така сама як і на вході.
Найбільш спрощене пояснення цього явища можна дати за допомогою співвідношення невизначенностей:
- ,
Якщо вважати, що положення частинки визначено з точністю до товщини бар’єру, при цьому виникає невизначенність по імпульсу, що може підвищити кінетичну енергію частинки, і зробити її достатньою для переходу через бар’єр. [5]
Ймовірність проходження бар'єру залежить від його висоти, і від енергії налітаючої частинки, але перш за все, від товщини бар'єру — проміжку, в якому потенційна енергія частинки більша за кінетичну (цю область називають класично недоступною областю). З ростом товщини, вона спадає експоненційно. При цьому, важливе співвідношення між довжиною дебройлівської хвилі частинки і товщиною бар'єру. Для важких частинок, таких як альфа-частинки, або протони, довжина хвилі є у тисячі разів меншою, ніж для електронів, а через це, ймовірність проходження навіть тонких бар'єрів є дуже малою. Наприклад, у ядрі радію альфа-частинка долає створений ядерними силами потенціальний бар'єр з ймовірністю лише 3•10-32, а для більш стабільних ядер ця величина ще менша[6]. З іншого боку, електрони провідності в напівпровідниках характеризуються ефективними масами, які можуть бути набагато меншими від маси вільних електронів, що дозволяє створювати тунельні діоди із шириною бар'єру в кілька десятків нанометрів.
Математичний опис[ред. | ред. код]

Розглянемо рівняння Шредінгера для одновимірної системи і прямокутного бар'єру товщиною a. Оскільки U є стаціонарним, ми можемо скористатись формою, незалежною від часу:
- ,
де Е — кінетична енергія частинки, - зведена стала Планка а U(x) — потенціальна енергія частинки. Будемо шукати розв'язки виду:
- ,
Тоді залежну від координати частину рівняння можна записати як
Оскільки U має прямокутну форму, можна записати його як
Для лівої ділянки, тобто, до зіткнення, рівняння має форму
Воно має два розв'язки, eikx і e-ikx, де . Таким чином, на цьому проміжку, функція має вигляд
- , де A і B — деякі коефіцієнти.
Аналогічно, всередині бар'єру, функція буде мати вигляд
- , де ,
При цьому, з фізичних міркувань, D=0, адже вираз при ньому експоненційно зростає при заглибленні в бар'єр, що не має сенсу. Ми можемо поєднати ці два рішення, виходячи з припущення про нерозривність хвильової функції та її першої похідної у точці 0. Таким чином, рівняння для φ буде мати наступний вигляд (A покладене рівним 1):
З цього рівняння видно, що сліва від бар'єру, хвильова функція представлена суперпозицією двох хвиль, хвилі, що рухається вправо (eikx) і хвилі, що рухається вліво (e-ikx). Ці компоненти можна співставити з падаючою і відбитою хвилею. Але з другого рівняння, для х>0, можна бачити, що хвильова функція проникає за бар'єр, і експоненційно спадає у цій зоні. Для великих значень x, амплітуда ймовірності частинки прямує до нуля. Так само, оскільки q прямує до нескінченності при зростанні U0, для нескінченно високого бар'єру тунелювання також не відбувається. Ці два випадки відповідають класичному переходу у поведінці частинки.
Також, з рівняння можна бачити, що амплітуда відбитої хвилі не є рівною нулю навіть у випадку E>U0, тобто, частинка може відбитися від бар'єру, висота якого є меншою за його кінетичну енергію. Це явище носить назву надбар'єрне відбиття. Розрахунки показують, що ймовірність пройти бар'єр, висота якого рівна енергії частинки — ½.[1]
Для обчислення ймовірності тунелювання через бар'єр зі складною формою, його розбивають на тонкі ділянки, які можна вважати прямокутними, а потім інтегрують отримані значення ймовірності по всій товщині бар'єру.
Для практичних обчислень часто використовують величину, коефіцієнт проходження бар’єру або коефіцієнт прозорості, що дорівнює для прямокутного бар’єру:
- ,
де
- , де a (ця величина близька до одиниці).
У випадку бар’єру довільної форми формула перетворюється на:
Значення[ред. | ред. код]
Зоряний нуклеосинтез[ред. | ред. код]
Температура і тиск в ядрах зірок є надзвичайно високими, проте недостатніми для того, щоб нуклони могли подолати кулонівський бар’єр. Проте, завдяки квантовому тунелюванню, навіть за таких умов існує невелика ймовірність подолання цього бар’єру. Через те, що ця ймовірність досить мала, в реакцію вступає лише невелика частина ядер, через що час життя зірок є дуже великим — середня тривалість життя вільного протону всередині Сонці складає близько шести мільярдів років.[7]
Оскільки під час первісного нуклеосинтезу елементи важчі за літій практично не утворювалися, саме під час зоряного нуклеосинтезу утворилися більшість елементів що складає Землю і наші тіла.
Радіоактивний розпад[ред. | ред. код]
Альфа-розпад відбувається коли альфа-частинка тунелює через потенційний бар’єр, що створюється ядерними силами. Після цього вона покидає ядро, що розганяється кулонівським відштовхуванням. Аналогічним чином ядро може покинути і поодинокий протон — в такому випадку це явище називається протонним випромінюванням.[8]
Альфа-розпад широко використовується в техніці — у детекторах диму, термоелектричних генераторах, у медицині, тощо.
Тунельні діоди[ред. | ред. код]
У діодах на основі вироджених напівпровідників, електрони тунелюють через p-n-перехід за низьких напруг, проте не можуть робити це за високих, через що вольт-амперна характеристика таких діодів має ділянку з від’ємною диференційною провідністю. Такі діоди знаходять застосування у високочастотних підсилювачах електричних коливань, а також, завдяки своїй стійкості до іонізаційного випромінювання, в космічній техніці.[9]
Тунелювання через оксидну плівку[ред. | ред. код]
Окислення багатьох металів, таких як алюміній, призводить до утворення на їх поверхні тонкої плівки оксиду, що має діелектричні властивості. Проте при з'єднанні двох провідників, електрони тунелюють через цей шар, завдяки чому забезпечується провідність точок механічного з'єднання провідників, наприклад, скрутки проводів. Схоже явище для надпровідників носить назву ефект Джозефсона.
Скануючий тунельний мікроскоп[ред. | ред. код]
У тунельних мікроскопах використовується тонке вістря, на кінці якого, в ідеалі, знаходиться лише один атом. Це вістря розміщується на невеликій відстані від досліджуваного зразка, і на нього подається струм. Оскільки між вістрям і зразком — порожнеча, струм, згідно класичної електродинаміки, не мав би текти. Проте, завдяки тунелюванню, електрони з вістря мають шанс перейти на зразок, і, тим самим, створити струм. Оскільки ця ймовірність експоненційно залежить від відстані між вістрям і атомами зразка, вимірюючи зміни струму під час переміщення вістря, можна дуже точно визначити рельєф поверхні зразка — аж до окремих атомів. [10]
Скануюча тунельна мікроскопія є одним з найбільш точних прямих методів дослідження матерії на таких масштабах.
Тунельна іонізація[ред. | ред. код]
Електрон в атомі знаходиться на дні потенціальної ями, і не може тунелювати з неї. Але, якщо помістити атом в однорідне електричне поле, то потенціальна яма стає асиметричною, і з одного її боку з'вляється потенціальний бар'єр скінченної ширини.[11]
Квантова біологія[ред. | ред. код]
Існують підстави вважати, що тунелювання може бути одним з причин спонтанного виникнення мутацій в ДНК. Наприклад, на це вказує значно менший рівень мутацій в бактерій, що вирощуються в середовищі, багатому на дейтерій — тунелювання дейтерію значно менш ймовірне ніж тунелювання протію.
З іншого боку, тунелювання задіяне і в процесах репарації ДНК.[12]
Рух дислокацій[ред. | ред. код]
Квантове тунелювання можливе не тільки у системах, що складаються з однієї частинки. Наприклад, рух дислокацій у кристалах також визначається, в тому числі, їх тунелюванням. При цьому нерідко тунелює лише частина дислокації, а решта підтягується за нею.[13]
Примітки[ред. | ред. код]
- ↑ а б в Туннельный еффект
- ↑ The STM (Scanning Tunneling Microscope) The forgotten contribution of Robert Francis Earhart to the discovery of quantum tunneling.(англ.)
- ↑ Friedrich Hund – discoverer of Hund’s rule [Архівовано 2017-02-02 у Wayback Machine.](англ.)
- ↑ Под знаком кванта, 2012, с. 238.
- ↑ Туннельный эффект(рос.)
- ↑ Под знаком кванта, 2012, с. 241.
- ↑ Образование атомных ядер(рос.)
- ↑ Атомне ядро. Радіоактивний розпад та перетворення ядер (PDF). Архів оригіналу (PDF) за 2 лютого 2017. Процитовано 25 січня 2017.
- ↑ Тунельний діод
- ↑ ОСНОВИ СКАНУЮЧОЇ ЗОНДОВОЇ МІКРОСКОПІЇ ТА СПЕКТРОСКОПІЇ
- ↑ ИОНИЗАЦИЯ ПОЛЕМ(рос.)
- ↑ Quantum Tunnelling to the Origin and Evolution of Life(англ.)
- ↑ АНАЛИЗ И МОДЕЛИРОВАНИЕ ПРОЦЕССА ДВИЖЕНИЯ ДИСЛОКАЦИЙ В МОНОКРИСТАЛЛАХ АЛЮМИНИЯ(рос.)
Джерела[ред. | ред. код]
- Федорченко А. М. Квантова механіка, термодинаміка і статистична фізика // Теоретична фізика. — К. : Вища школа, 1993. — Т. 2. — 415 с.
- Леонид Пономарев. Глава 15 // Под знаком кванта. — 4. — М. : "Физматлит", 2012. — 464 с. — ISBN 978-5-9221-1368-7.
- Вакарчук I. О. Найпростіші задачі квантової механіки // Квантова механіка. — 4. — Львів : ЛНУ імені Івана Франка, 2012. — 872 с. — ISBN 978-966-613-921-7.
















