Золотий перетин

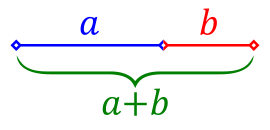
φ = (a+b) : a = a : b

У математиці та мистецтві дві величини утворюють золоти́й пере́тин (лат. Sectio aurea, англ. Golden ratio), якщо співвідношення їх суми і більшої величини дорівнює співвідношенню більшої і меншої. Це відношення прийнято позначати грецькою буквою $\varphi\,$.

Золотий перетин вважається співвідношенням найвідповіднішим естетичному сприйняттю зображення, вперше запропоноване давньогрецьким математиком Евклідом. Вживається в мистецтві й архітектурі, найчастіше як золотий прямокутник. Золотий прямокутник утворюється при поділі відрізку АВ в такій точці О, що площа прямокутника, одною стороною якого є весь відрізок, а іншою - менший з відрізків, дорівнює площі квадрата з більшим відрізком як стороною (|АВ| * |OB| = |АO|²).

$\varphi = \frac{AO + OB}{AO} = \frac{AO}{OB}$

Це рівняння має єдиний додатній розв'язок

$\varphi = \frac{1 + \sqrt{5}}{2} \approx 1.61803398874989484\dots$

Відношення двох відрізків приблизно дорівнює 13:8.

Число $\varphi\,$ деколи називають золотим числом.

Наближення

Наближення Золотого перетину з точністю 150 знаків після десяткової коми:

1.61803 39887 49894 84820 45868
  34365 63811 77203 09179 80576
  28621 35448 62270 52604 62818
  90244 97072 07204 18939 11374
  84754 08807 53868 91752 12663
  38622 23536 93179 31800 60766

Математичні властивості

Обчислення значення золотого перетину

Золотий перетин $\varphi$ можна обчислити безпосередньо з означення:

$\frac{a+b}{a} = \frac{a}{b} = \varphi\,.$

Праве рівняння дає $a=b\varphi\,$. Підставляючи цю рівність у ліву частину:

$\frac{b\varphi+b}{b\varphi}=\frac{b\varphi}{b}\,.$

Скоротивши $b\,$ отримаємо:

$\frac{\varphi+1}{\varphi}=\varphi.$

Помноживши обидві частини на $\varphi\,$ після перестановки отримаємо:

φ² − φ − 1 = 0.

Це квадратне рівняння має два розв'язки, один з яких є додатнім

$\varphi = \frac{1 + \sqrt{5}}{2} \approx 1.61803\,39887\dots\,$

Зв'язок із числами Фібоначчі

Спіраль Фібоначчі

Золотий перетин є границею відношення двох сусідніх членів у послідовності Фібоначчі:

$\lim_{n\to\infty}\frac{F_{n+1}}{F_n}=\varphi.$

При цьому члени послідовності $\frac{F_{n+1}}{F_n}$ збігаються до $\varphi\,$ поперемінно — один елемент знизу, наступний згори і т.д. Наприклад

$\frac{F_6}{F_5}=\frac{8}{5}=1,6<\varphi<\frac{F_7}{F_6}=\frac{13}{8}=1,625$

Формула Біне виражає за допомогою $\varphi\,$ значення числа Фібоначчі $F_n\,$ в явному вигляді:

$F_n = \frac{\varphi^n - (-\varphi )^{-n}}{\varphi - (-\varphi )^{-1}} = \frac{\left(\frac{1 + \sqrt{5}}{2}\right)^n - \left(\frac{1 - \sqrt{5}}{2}\right)^n}{\sqrt{5}}\approx\frac{\phi^n}{\sqrt{5}}\quad (n\geq 1).$

Окрім цього, послідовні степені числа $\varphi\,$ задовільняють рекурентному співвідношенню ідентичному до чисел Фібоначчі:

$\varphi^{n+2} = \varphi^{n+1} + \varphi^n.\,$

Спіраль Фібоначчі (див. рисунок) є наближенням золотої спіралі.

Золотий перетин у пентаграмі

Червоний : Зелений =
Зелений : Синій =
Синій : Фіолетовий = $\varphi\,$

Золотий перетин виступає у правильній пентаграмі, який вважався магічним символом у багатьох культурах. Точка перетину сторін ділить їх у золотій пропорції. Більша частина сторони також ділиться у золотій пропорції іншою точкою перетину.

Пентаграм містить п'ять гострокутних та п'ять тупокутних золотих трикутників. У кожному з них співвідношення довжини довшої та коротшої сторони утворює золотий перетин.

Посилання

• Про красу користі і користь краси (Дзеркало тижня)
• Золотий перетин на www.photobattle.com.ua
• К.В. Киркач, Золотий перетин у дизайні освітлювальних установок (Світло-люкс)
• А. Д. Бердукидзе, Золотое сечение Квант №8, 1973 (рос.)

Див. також

• Модулор
• Трикутник Кеплера
• Правило третин