Теорема Белла
| Квантова механіка |
|---|
|
Вступ · Історія Математичні основи[en] |
|
Фундаментальні поняття |
|
Наближені методи |
|
Відомі науковці |
Теорема Белла — теоретичне твердження, яке встановлює важливу відмінність між передбаченнями квантової механіки та класичної фізики, і показує, що жодна теорія з локальними прихованими параметрами[en] не може відтворити квантовомеханічні результати[1]. Експериментальні перевірки теореми Белла досі підтверджували справедливість квантовомеханічного підходу.
Принциповою відмінністю квантовомеханічного підходу від класичного є те, що квантова механіка використовує поняття амплітуди ймовірності, величини комплексної. Класична фізика, навіть коли точне значення параметрів невідоме, оперує лише дійсними ймовірностями. Дійсність ймовірності накладає обмеження на значення деяких кореляторів у класичній фізиці. Ці обмеження називають нерівностями Белла. Опис через амплітуди ймовірностей у квантовій механіці не має цих обмежень. Тобто, у квантовій механіці можна отримати результати несумісні з класичними, які б локальні приховані параметри класичний підхід не використовував.
Написана Джоном Беллом у 1964 році стаття «Про парадокс Ейнштейна — Подольського — Розена»[2][3] є тим, що тепер називають теоремою Белла. Ще під час навчання Белл зацікавився основами квантової механіки, а особливо — ідеєю відділення класичного поняття про кота Шредінгера від квантового. У період між закінченням Королівського Університету та 1952 роком Белл був прибічником радикальних поглядів стосовно квантової механіки.
Точно не відомо, що стало основною причиною для створення даної статті, але в розділі «Вдячності» в роботі під назвою «Про проблему прихованих параметрів у квантовій механіці» (On the Problem of Hidden Variables in Quantum Mechanics), він написав: «Перші ідеї цієї статті з'явились у 1952 році. Я дуже вдячний доктору Ф. Мендл за цікаву дискусію в цей період».
Історичне тло[ред. | ред. код]
На початку 1930-х філософські висновки чинної інтерпретації квантової теорії бентежили багатьох тодішніх визначних фізиків, зокрема Альберта Ейнштейна. 1935 року Ейнштейн разом із Борисом Подольським та Натаном Розеном опублікували статтю про парадокс Ейнштейна — Подольського — Розена (ЕПР), яким продемонстрували, що квантовомеханічний опис начебто не є повним. Постала надія можливого відкриття в майбутньому повнішої й зрозумілішої теорії. Цей висновок опирався на начебто розумні припущення «локальності (близькодії)» та «реалізму», разом — «локального реалізму» або ж, іншими словами, на припущення про існування локальних прихованих параметрів. Мовою Ейнштейна локальність означала неможливість миттєвої (страхітливої) далекодії, а реалізм означав, що місяць на небі є навіть тоді, коли на нього ніхто не дивиться. Ці припущення були темою палких дискусій серед фізиків, зокрема між нобелівськими лауреатами Ейнштейном та Нільсом Бором.
Революційна робота 1964 року «On the Einstein Podolsky Rosen paradox»[2] Джона Стюарта Белла розглянула ситуацію, аналогічну гіпотетичному парадоксу ЕПР на основі вимірювання спінів сплутаних електронів. Виходячи з міркувань Ейнштейна та його колег, говорив Белл, вибір налаштувань вимірювання в одному місці не повинен впливати на результат в іншому (і навпаки). Сформулювавши описані так локальність та реалізм математично, він показав, що виникають ситуації, в яких такий висновок буде несумісним із квантовомеханічними розрахунками.
Експериментальні перевірки методом, запропонованим Беллом, що замість сплутаних електронів використовували сплутані фотони, провели Джон Клаузер із Стюартом Фрідменом[en] (1972) і Ален Аспе та інші (1981). Вони продемонстрували, що передбачення квантової механіки в цьому аспекті справедливі. Щоправда, вони спиралися на припущення, які залишали прогалини для локального реалізму.
У жовтні 2015 року Генсен зі співробітниками[4] повідомили, що вони поставили експеримент, який не залишає прогалин, і який може змусити відкинути принаймні один із принципів: локальності, реалізму чи свободи волі (принцип свободи волі є альтернативою теоріям жорсткого детермінізму). Дві з цих логічних можливостей: нелокальність та нереалізм, відповідають добре розробленим інтерпретаціям квантової механіки й мають чимало прихильників, на відміну від третього: відмови від свободи волі. Майбутні експериментальні підтвердження порушення нерівностей Белла можуть значно звузити клас прийнятних детерміністичних теорій, але не можуть фальсифікувати абсолютний детермінізм, який сам Белл описав так: «… це не просто бездушна природа, керована прихованим від ока механізмом, це означає, що й наша власна поведінка, включно з вірою в те, що ми можемо вибирати який експеримент поставити, уже наперед визначена.»
Загальний огляд формулювання[ред. | ред. код]

Теорема Белла стверджує, що будь-яка теорія з прихованими параметрами не може відтворити усіх передбачень квантової механіки. Її зазвичай доводять для квантової системи сплутаних кубітів. Популярними об'єктами є частинки зі спіном або поляризацією. Квантова механіка дозволяє передбачити кореляції, що спостерігалися б, якщо вимірювали б різні проєкції спіна чи поляризації. Белл показав, що якби справедливою була теорія з прихованими локальними параметрами, то кореляції мали б задовольняти певним обмеженням, які називають нерівностями Белла. А для квантових кореляцій цих обмежень немає, тому в квантовій механіці можуть виникати ситуації, що не відтворюються теорією з локальними прихованими параметрами.
У роботі[2] Белл розглянув пару частинок із напівцілим спіном і припустив, що в початковий момент стану частинки перебувають у синглетному стані, а потім починають розлітатися в різних напрямках. На великій відстані від початкового положення робляться вимірювання проєкції спіну на осі, вибір яких у різних детекторах незалежний. Результатами кожного вимірювання можуть бути значення спіну вгору (+) та спіну вниз (-).
Ймовірність того, що в двох місцях буде отримано однакові результати, залежить від відносного кута вимірювання двох спінів. Вона лежить між нулем та одиницею для всіх кутів, крім 0° та 180°. Оскільки повний кутовий момент зберігається, а в синглентому стані спін дорівнював нулю, ймовірність отримати однакові показники при паралельній (антипаралельній) орієнтації детекторів дорівнює одиниці. Це передбачення однакове як у класичній, так і в квантовій механіці.
Втім, теорема Белла стосується середніх значень, обрахованих за результатами багатьох таких вимірювань. Кореляцію двох парних змінних у квантовій механіці зазвичай визначають як середнє добутку пари вимірювань. Це означення відрізняється від звичного означення статистики. Спільними рисами є те, що для будь-якого означення, коли пари результатів завжди однакові, то кореляція дорівнює +1, коли вони завжди протилежні, то кореляція дорівнює -1, а коли результати вимірювання збігаються у 50 % випадків, кореляція дорівнює 0.
Вимірювання спінів сплутаних частинок в антипаралельному напрямку, тобто вздовж одної осі, але в протилежних напрямках, дає повну кореляцію. Якщо вимірювання робити вздовж паралельних напрямків, вони завжди дають протилежний результат, і численні вимірювання демонструють ідеальну антикореляцію. Усе це повністю узгоджується з описаними вище випадками. Нарешті, якщо детектори орієнтовані перпендикулярно, то ймовірність збігу результатів буде 50 %, і множина вимірювань некорельована. Ці опорні випадки ілюструє наступна таблиця. Стовпчики в ній — приклади пари значень, які Аліса та Боб можуть записати. Час зростає вправо.
| Антипаралельні | Пара 1 | Пара 2 | Пара 3 | Пара 4 | … | Пара n | |
|---|---|---|---|---|---|---|---|
| Аліса, 0° | + | − | + | + | … | − | |
| Боб, 180° | + | − | + | + | … | − | |
| Кореляція = ( | +1 | +1 | +1 | +1 | … | +1 | ) / n = +1 |
| (100 % однакові) | |||||||
| Паралельні | Пара 1 | Пара 2 | Пара 3 | Пара 4 | … | Пара n | |
| Аліса, 0° | + | − | − | + | … | + | |
| Боб, 0° or 360° | − | + | + | − | … | − | |
| Кореляція = ( | -1 | -1 | -1 | -1 | … | -1 | ) / n = -1 |
| (100 % протилежні) | |||||||
| Ортогональні | Пара 1 | Пара 2 | Пара 3 | Пара 4 | … | Пара n | |
| Аліса, 0° | + | − | + | − | … | − | |
| Боб, 90° or 270° | − | − | + | + | … | − | |
| Кореляція = ( | −1 | +1 | +1 | −1 | … | +1 | ) / n = 0 |
| (50 % однакові, 50 % протилежні) |
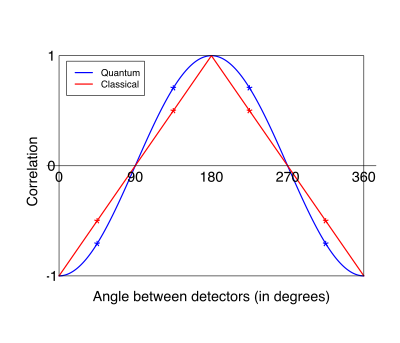
Коли орієнтація детекторів проміжна між цими опорними випадками, існування прихованих локальних змінних могло б узгоджуватися з лінійною залежністю кореляцій від кута, але відповідно до нерівності Белла, не може досягнути залежності, яку передбачає квантова теорія, а саме — того, що кореляції залежать від кута як мінус косинус. Експериментальні результати узгоджуються з передбаченнями квантової механіки[1].
Із часом теорема Белла багато разів перевірялася експериментально. Однак, у них виявляли різноманітні прогалини, включно з прогалиною детектування[5] та прогалиною комунікації[5]. Поступово експерименти покращувалися й стали перекривати ці прогалини. 2015 року було проведено перший експеримент, який закрив усі з них[4].
На сьогодні вважається, що теорема Белла має доволі значну кількість доказів, і прихильників локальних прихованих параметрів залишилося небагато, хоча теорему постійно й ретельно вивчають, критикують і уточнюють[6][7].
Загальні зауваження[ред. | ред. код]
Порушення нерівностей Белла дає майже беззаперечну демонстрацію того, що вже сильно підозрювалось: квантова фізика не може бути відтворена жодним варіантом класичної фізичної картини[8]. Раніше з класичною фізикою здавалися несумісними принцип доповнюваності та колапс хвильової функції. Порушення нерівностей Белла показують, що жодне розв'язання таких проблем не може здолати дивизну квантової поведінки[9].
Стаття про парадокс ЕПР «вказала» на незвичні властивості сплутаних станів, наприклад, згаданого синглетного стану, які стали основою для сучасних застосувань квантової фізики, таких як квантова криптографія.
Сильним пунктом теореми Белла є те, що вона не спирається на жодну конкретну фізичну теорію. Вона показує, що природа порушує саме загальні та фундаментальні припущення класичної картини світу, а не просто якісь окремі моделі. Жодна комбінація локальних детермінованих та локальних випадкових змінних не може відтворити явища, передбачені квантовою механікою й підтверджені численними експериментами[10].
Див. також[ред. | ред. код]
Джерела[ред. | ред. код]
- ↑ а б C.B. Parker (1994). McGraw-Hill Encyclopaedia of Physics (вид. 2nd). McGraw-Hill. с. 542. ISBN 0-07-051400-3. Сам Белл написав: «якщо [теорія з прихованими параметрами] локальна, то вона не узгоджується з квантовою механікою, а якщо вона узгоджується з квантовою механікою, то вона не може бути локальною. Ось що стверджує теорема.» John Bell, Speakable and Unspeakable in Quantum Mechanics, Cambridge University Press, 1987, p. 65.
- ↑ а б в Bell, John (1964). On the Einstein Podolsky Rosen Paradox (PDF). Physics. 1 (3): 195—200.
- ↑ Reprinted in JS Bell (2004). Chapter 2:On the Einstein-Podolsky-Rosen paradox. Speakable and Unspeakable in Quantum Mechanics: Collected Papers on Quantum Philosophy (вид. Alain Aspect introduction to 1987). Cambridge University Press. с. 14—21. ISBN 978-0521523387.
- ↑ а б Hensen, B; Bernien, H; Dréau, AE; Reiserer, A; Kalb, N; Blok, MS; Ruitenberg, J; Vermeulen, RF; Schouten, RN; Abellán, C; Amaya, W; Pruneri, V; Mitchell, MW; Markham, M; Twitchen, DJ; Elkouss, D; Wehner, S; Taminiau, TH; Hanson, R. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature. 526: 682—686. arXiv:1508.05949. Bibcode:2015Natur.526..682H. doi:10.1038/nature15759. PMID 26503041.
- ↑ а б Article on Bell's Theorem by Abner Shimony in the Stanford Encyclopedia of Philosophy, (2004).
- ↑ Griffiths, David J. (1998). Introduction to Quantum Mechanics (вид. 2nd). Pearson/Prentice Hall. с. 423.
- ↑ Merzbacher, Eugene (2005). Quantum Mechanics (вид. 3rd). John Wiley & Sons. с. 18, 362.
- ↑ Penrose, Roger (2007). The Road to Reality. Vintage Books. с. 583. ISBN 0-679-77631-1.
- ↑ Abers, E. (2004). Quantum Mechanics. Addison Wesley. с. 193—195. ISBN 9780131461000.
- ↑ R.G. Lerner; G.L. Trigg (1991). Encyclopaedia of Physics (вид. 2nd). VHC publishers. с. 495. ISBN 0-89573-752-3.
