Аеродинаміка
Аеродина́міка — розділ механіки суцільних середовищ, в якому метою досліджень є вивчення закономірностей руху повітряних потоків та їх взаємодії з перешкодами та рухомими тілами. Загальнішим розділом механіки є газова динаміка, в якій вивчаються потоки різних газів. Традиційно до газової динаміки відносять по суті задачі аеродинаміки при русі тіл зі швидкостями, що близькі або перевищують швидкість звуку в повітрі. При цьому важливо враховувати стисливість повітря.
Дослідження в аеромеханіці пов'язані з визначенням таких характеристик потоків як швидкість частинок середовища, густини, тиску, температури як функцій простору і часу. Після їх визначення в кожній конкретній ситуації стає можливим обчислення сил та моментів сил, що діють на тіло в потоці. Як наукова дисципліна аеродинаміка послуговується базою для вирішення широкого кола прикладних задач. Перелік практичних проблем, при вирішенні яких виникають і розв'язуються конкретні задачі аеродинаміки, досить довгий і включає не лише проблеми авіації, а й проблеми ракетобудування, наземного та морського транспорту, метеорології, екології, сільського господарства, містобудування та ін. Для одержання відповіді на питання в аеродинаміці використовуються експериментальні та теоретичні методи. Особливого значення в сучасних умовах набувають методи комп'ютерної аеродинаміки. Серед багатьох питань, на які сучасна аеромеханіка дає змістовні відповіді пізнавально найбільш цікаві, за висловом видатного вченого Т. Кармана[1] це питання «Чому ми можемо літати»? та «Як ми можемо літати»? Існує багато питань, на які сучасна аеродинаміка намагається дати відповіді і при обговоренні цих питань формується ряд важливих проблем сучасного природознавства. Зараз вважається, що аеродинаміка в своєму розвитку вступила в комп'ютерну епоху. У дослідників з'явилися досить потужні засоби для одержання кількісних оцінок характеристик течій в рамках вибраної математичної моделі. Однак величезний обсяг інформації, який здобувається методами комп'ютерної динаміки рідин та газів, для свого аналізу і розуміння вимагає від дослідника глибокого розуміння фізики процесів, глибинних причинно-наслідкових зв'язків. Саме ця обставина уможливила появу досить глибоких досліджень змісту понять, які, здавалося, є давно усталеними. Цікаві нові результати по аналізу основ аеродинаміки представлено в[2]
У суспільстві існує великий інтерес, як до певних фундаментальних проблем аеродинаміки, так і до широкого кола прикладів практичного застосування знань в галузі аеродинаміки. Великий набір предметних питань з відповідями в стилі популяризації науки представлено на сайті Національного космічного агентства США[3]. Ця стаття лише перший крок в представленні проблем аеродинаміки в Вікіпедії. Подальше розширення інформаційного поля має базуватися на статтях Аеродинаміка літака, Аеродинаміка крила, Підйомна сила, Аеродинамічний опір, Примежовий шар та інших.
В цьому розділі відмічено лише певні важливі моменти в формуванні розуміння основних закономірностей аеродинаміки. Багата подіями історія гідромеханіки не може бути висвітлена в короткій статті. Певні важливі моменти в історії після першого польоту літака будуть відмічені в відповідних розділах.
Роздуми людини над аеродинамічними по суті проблемами, мабуть, мали місце в далекі доісторичні часи. Все починалося з природного бажання стародавньої людини повторити політ птаха в повітрі. Про це свідчить і широко відомий давньогрецький міф про Дедала та Ікара. Але перші кроки, які започаткували рух до сучасної наукової аеродинаміки, були зроблені лише в елліністичний період розвитку давньогрецької культури. Особливо слід відзначити Арістотеля, який зрозумів, що повітря має вагу. Разом з досягненнями Архімеда в розумінні сутності плавання тіл, це дійсно формувало підвалини для постановки та розв'язання проблеми польоту об'єктів, що важчі за повітря.

Значні подальші кроки в розвитку аеродинаміки пов'язані з діяльністю видатної особистості — Леонардо да Вінчі. Він зрозумів, що саме рух крила відносно повітря є причиною виникнення підйомної сили. Він запропонував декілька проєктів орнітоптерів, пристроїв, що мали копіювати поведінку крил птахів під дією мускульної сили людини. Жоден з цих проєктів не було реалізовано. Серед інших його розробок були проєкти парашута та гелікоптера. При аналізі явища виникнення аеродинамічного опору він ввів концепцію добре обтічного тіла. Перший в історії політ людини в повітрі було здійснено в 1783 році Братами Монгольф'є на повітряній кулі, наповненій гарячим повітрям. В цей час уже було накопичено досить глибокі знання про закономірності взаємодії потоку з твердими тілами, які суттєво просували людство до створення літального апарату, важчого за повітря. Серед досягнень фундаментальної аеродинаміки відмітимо встановлену Галілеєм пропорційність між аеродинамічним опором і густиною повітря (1600 р.). Французький вчений Едм Маріот встановив пропорційність аеродинамічного опору квадрату швидкості руху тіла (1673 р.).
Значний вплив на розвиток аеродинаміки мала робота І. Ньютона по визначенню сили, що діє на тіла різної форми з боку набігаючого потоку. Досить складна, с точки зору сучасних уявлень про структуру обтікаючого потоку, задача була легко розв'язана Ньютоном на основі досить специфічної гіпотези про взаємодію частинок повітря з обтічною поверхнею. Використання цієї гіпотези для плоскої пластинки дає наступну формулу для величини сили: , де — густина повітря, — площа пластинки, -швидкість набігаючого потоку, — кут нахилу пластинки до напрямку потоку. Сила направлена перпендикулярно до пластинки. Ця формула знана як закон квадрата синуса.
Пропорційність квадрату синуса величини підйомної сили (складова сили , перпендикулярна до напрямку потоку) вказувала на практичну неможливість створення літака. З неї витікала дуже завищена оцінка площі крила і, відповідно, ваги літального апарату. Експериментальні дослідження не підтвердили формулу Ньютона, однак його авторитет був настільки високим, що на її критику мало хто відважувався. Як вказано в[1], багато авторів вважало, що помилковість формули Ньютона затримала розвиток авіації на багато років. Однак це не зовсім так. Не менш важливим стримуючим фактором в розвитку авіації була відсутність ефективного двигуна. Врешті-решт на початку двадцятого століття (1903 рік) в повітря піднявся літак братів Райт і розвиток авіації пішов «семимильними кроками». Розповідь про історію створення літака братами Райт представлено в фільмі https://www.youtube.com/watch?v=uB-swWvAUZI [Архівовано 9 грудня 2015 у Wayback Machine.]. Створенню літака та здійсненню першого польоту передував великий об'єм експериментальних досліджень. Існує численна література (швидше пропагандистського характеру) в якій відстоюється пріоритет першого польоту літака А. Ф. Можайського. Однак, серйозні дослідження, в тому числі виконані в ЦАГІ ім. М. Е. Жуковського не дають підстав довіряти свідченням підібраних журналістами свідків[4]. Історія розвитку аеродинаміки, як наукової основи технічних рішень, та авіації багата великою кількістю драматичних подій, включаючи боротьбу за пріоритети. Детальний аналіз цієї історії можна знайти в[5]. Змістовний, але скорочений історичний нарис стосовно розвитку досліджень в галузі механіки рідини і газу представлено в популярному підручнику[6]. Змістовний, з великою кількістю цікавих фактів, нарис історії повітроплавання представлено в книзі відомого українського планериста Віктора Гончаренка[7]
Розуміння закономірностей обтікання тіла потоком формується на встановленні зв'язків між силами та моментами, що діють на тіло з формою самого тіла, його орієнтацією відносно набігаючого потоку та властивостями збуреного потоку (розподіл в просторі та зміни в часі швидкостей, тиску, густини, температури).
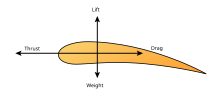
На малюнку приведено лише головні вектори сил, що діють на тіло в потоці. Тут показано чотири сили: сила тяги, що генерується рушієм, сила опору з боку повітря, підйомна сила та сила ваги. Слід мати на увазі, що для літальних апаратів лінії дії вказаних чотирьох сил не перетинаються в одній точці. Тому при аналізі аеродинаміки конкретних конструкцій велике значення мають величини моментів сил, які обчислюються, наприклад, відносно центру мас літального апарату. Для оцінки властивостей руху, а, особливо, для ефективного керування рухом, слід брати до уваги фактичний розподіл тиску по поверхні тіла. При вирішені задачі по визначенню вказаних характеристик фізичних полів гіпотетично можна сподіватися на використання експериментальної техніки. Саме такий шлях використано братами Райт при створенні першого літака. Відсутність глибокого розуміння закономірностей аеродинаміки вони компенсували великим обсягом виконаних експериментів.
Однак, як показав історичний досвід, значно швидше і ефективніше необхідні знання формуються на основі результатів математичного моделювання з використанням відповідних моделей повітряного середовища. Практично використовуються різні моделі в залежності від умов обтікання. В основі практично всіх моделей лежить припущення про можливість заміни реального середовища певним континуумом, тобто суцільним середовищем. Така заміна з великим успіхом використовується в багатьох розділах фізики. Цікава оцінка методичної ефективності гіпотези суцільного середовища дана Л. Й. Мандельштамом[8]. Викладаючи результат Дебая по оцінці теплоємності кристала, одержаний з використанням моделі суцільного середовища він зауважив «Він (Дебай) зробив явно невірну, але геніальну річ.» (Лекція 29).
Що стосується об'єктів, що обтікаються потоком повітря, то в величезній більшості випадків вони розглядаються як абсолютно тверді тіла, що не деформуються під дією аеродинамічних сил. Однак випадки, коли слід враховувати деформації тіл під впливом аеродинамічних сил досить важливі. Тут слід вказати не лише на очевидний факт коливання полотнища прапора під дією вітру. Набагато важливішим є явище флатеру, з яким пов'язано виникнення дуже небезпечних коливань крила літака при певних швидкостях польоту. Гіпотеза про недеформовність поверхні обтічного тіла дає можливість чітко записати умови на його поверхні при математичному моделюванні в задачах аеродинаміки.
При дослідженні потоків газу чи рідини вивчають розподіл та зміни в просторі-часі таких характеристик як швидкість, густина, тиск, температура. Що стосується способів опису руху середовища, то в механіці суцільного середовища розрізняють два підходи, які пов'язують з іменами Ейлера та Лагранжа[9]. Згідно Ейлерового підходу об'єктом дослідження є кінематичні характеристики потоку в певних вибраних точках об'єму, зайнятого потоком. В цьому випадку координати точки фіксуються і розглядається зміна в часі вектора швидкості. В підході Лагранжа прослідковується історія руху певної точки середовища в часі. Такий опис руху природно використовувати при записі основних фізичних законів, які пов'язані з рухом матеріальної точки. Між характеристиками потоку по Лагранжу та Ейлеру є взаємно однозначна відповідність.
Важливим положенням аеродинаміки є принцип зворотності. Зазвичай цей принцип використовується в фізиці для опису закономірностей, які не змінюються при зміні напрямку часу. В аеродинаміці приймається, що характеристики сил взаємодії будь-якого тіла і повітря (газу) будуть однакові в обох випадках: коли тіло рухається в нерухомому повітрі, чи коли на нерухоме тіло набігає рівномірний потік повітря.
Повітря — суміш газів, складається з молекул ряду хімічних елементів елементів, серед яких — азот (78 %), кисень (21 %) і решта: вуглекислий газ, водень, аргон та інші. Фізичні властивості повітря та його склад суттєво змінюються зі збільшенням відстані від землі. Ця обставина особливо важлива при вирішенні проблем аеродинаміки в авіації та ракетній техніці. Важливість врахування змін властивостей повітря з висотою зумовило введення міжнародного стандарту. На рисунку показано основні властивості такої стандартної атмосфери.

В число параметрів, що задаються стандартною атмосферою входять: висота, температура, швидкість звуку, тиск, густина, кінематична в'язкість. Звичайно, така статична стандартна атмосфера є результатом усереднення багатьох спостережень та замірів. В дійсності реальна атмосфера надзвичайно мінлива динамічна система, в якій характеристики можуть змінюватися в широких межах. Закономірності процесів, що відбуваються в атмосфері, вивчаються в такій дисципліні, як фізика атмосфері океану. В більшості випадків для аналізу процесів взаємодії атмосфери та рухомого об'єкту атмосферу розглядають як однорідне середовище. Для проведення обчислень можна використовувати дані про властивості атмосфери на певній висоті.
Для обчислення значень фізичних параметрів створено спеціальні он-лайнові калькулятори (http://www.luizmonteiro.com/StdAtm.aspx [Архівовано 22 квітня 2011 у Wayback Machine.]). Використовуючи цей калькулятор можна, наприклад, знайти оцінки середню довжину вільного пробігу молекул в повітрі на різних висотах. На рівні поверхні моря маємо . На висоті 80 км . Малість цієї величини відносно характерних розмірів більшості рухомих об'єктів в атмосфері є певною підставою для використання моделі суцільного середовища при дослідженні аеродинамічних явищ навіть на висоті 80 км. Для аналізу таких явищ на значно більших висотах використовують методи молекулярної газової динаміки. [10]
Математичні моделі в теоретичній аеродинаміці формулюються в залежності від особливостей руху. Важливе значення для вибору моделі має така характеристика потоку як число Маха . Цим числом визначаться співвідношення між величиною характерної швидкості потоку (це може бути швидкість рівномірного потоку, що набігає на тіло) та швидкістю звуку в повітрі. Ця остання величина суттєво змінюється з висотою. Скориставшись вказаним вище калькулятором для визначення характеристик стандартної атмосфери одержуємо, наприклад, такі значення швидкості звуку для шару на рівні моря (=340,294 м/с) та на висоті 10000 м (=299,532м/с). Значення числа Маха є визначальним, як з точки зору класифікації потоків, так і з точки зору вибору основних припущень при формуванні математичних моделей аеродинаміки.
В аеродинаміці використовують наступні моделі середовища:
1. Ідеальний нестисливий газ. Із властивостей реального газу в цій моделі враховується лише існування маси частинки середовища.
2. В'язкий нестисливий газ. В моделі враховується притаманна реальним газам властивість наявності опору при зсуві шарів газу. В більшості випадків врахування в'язкості газу проводиться в рамках моделі Ньютона.
3. Ідеальна стислива рідина (газ). Така модель дуже широко використовується в акустиці. Як правило в процесах, пов'язаних з генерацією та поширенням звукових хвиль числа Маха дуже малі в порівнянні з одиницею.
4. В'язкий стисливий газ. В рамках цієї моделі аеродинамічні процеси можуть бути описані найбільш повно. Однак, при цьому математичні задачі виявляються досить складними.
Використання тієї чи іншої моделі визначається метою формулювання задачі досліджень. В багатьох випадках мова може йти про якісний аналіз процесу обтікання, коли не ставиться задача визначення кількісних характеристик потоку. Як приклад, можна вказати на використання моделі ідеального газу для встановлення механізму генерації підйомної сили при обтіканні крила.
Для класифікації потоків в аеродинаміці вибираються різні критерії. Перш за все важливою є класифікація, пов'язана з числом Маха. Якщо число Маха в усіх точках існування потоку менше одиниці, потік характеризують як дозвуковий. В багатьох випадках можлива така ситуація, коли в частині області, зайнятої потоком, число Маха менше одиниці, а в решті потоку — більше одиниці. Такі потоки характеризують як трансзвукові. Якщо в усій області потоку швидкість частинок газу перевищує локальну швидкість звуку потік характеризують як надзвуковий. Часто використовується термін гіперзвук, коли мається на увазі потоки з числами Маха значно більшими одиниці (наприклад М більше 5). Границя між гіперзвуком та надзвуком досить розмита. Слід розрізняти поняття гіперзвуку в аеродинаміці та акустиці.

Для класифікації потоків використовують також їх певні структурні особливості і розрізняють ламінарні потоки та турбулентні потоки.
В багатьох випадках при формуванні потоку ефект в'язкості виявляється не суттєвим. Тому розрізняють в'язкі і нев'язкі потоки.
За структурою течії навколо твердого тіла розрізняють відривні та безвідривні потоки.
Певна різниця в підходах до вивчення характеристик потоків виникає при врахуванні геометричних параметрів, що характеризують аеродинамічну ситуацію. Якщо геометрія потоку така, що можна скористатися моделлю нескінченного простору, заповненого газом, в якому рухається тіло (літак, ракета, автомобіль), говорять про зовнішню аеродинаміку. Коли характеристики потоку суттєво визначаються каналами, в яких рухається газ, говорять про внутрішню аеродинаміку. Задачі внутрішньої аеродинаміки виникають при аналізі роботи реактивних двигунів, газових та парових турбін.
В залежності від швидкості набігаючого потоку в околиці обтічного тіла формуються різного типу структури. Чаруючий світ різного типу течій представлено в унікальній книзі Мілтона Ван-Дайка[11]. Сучасні методи візуалізації потоків дають можливість одержати ще більш вражаючі кольорові зображення різноманітних явищ в потоках рідин та газів[12]. Значна кількість візуалізованих зображень потоків доступна для перегляду в Інтернет https://web.archive.org/web/20150402092327/http://cfd.spbstu.ru/agarbaruk/gallery.html.
Закони збереження — основа математичних моделей
[ред. | ред. код]Коли йдеться про вивчення руху частинки рідини чи газу основним співвідношенням в математичній моделі для його описання є співвідношення другого закону Ньютона. Однак, у зв'язку з деформовністю середовища, з можливістю зміни відносних відстаней між частинками середовища в процесі руху другий закон Ньютона необхідно доповнювати додатковими законами збереження для формування повної системи рівнянь математичної моделі. Перш за все, це закони збереження загальні для всіх розділів механіки — закон збереження енергії, закон збереження імпульсу та закон збереження моменту імпульсу. Записані з використанням термінів і понять, які використовуються при побудові математичної моделі явища, закони збереження часто дають можливість сформулювати важливі загальні висновки відносно руху системи.
При вивченні рухів рідин та газів загальні закони збереження доповнюються іншими співвідношеннями, які теж виражають факт «збереження» певних характеристик потоку і називаються по різному — законами, принципами, рівняннями. Перш за все слід вказати на найважливіше співвідношення, яке присутнє в усіх моделях механіки суцільного середовища — це рівняння нерозривності, яке можна розглядати як конкретну форму запису закону збереження маси. Якщо для компонентів вектора швидкості частинок середовища використати декартові компоненти позначити густину середовища як , то рівняння нерозривності набуває вигляду
Це співвідношення виражає простий факт — приток рідини чи газу в виділений об'єм компенсується зміною густини середовища. Оскільки це співвідношення формується при розгляді певного фіксованого об'єму воно записане в змінних Ейлера.
Рівняння нерозривності (збереження маси) має досить універсальний характер і має прийматися до уваги при математичному моделюванні будь-яких суцільних середовищ. Його вигляд незмінний для всіх середовищ — води, повітря, металу. Якщо при русі середовища необхідно враховувати його стисливість рівняння нерозривності включає чотири характеристики стану середовища — густину та три компоненти вектора швидкості. Для нестисливої величини рівняння зв'язує значення трьох компонент вектора швидкості.
Знання про властивості потоку газу та сили взаємодії потоку з різними тілами здобуваються в аеродинаміці різними шляхами. На основі певних припущень про властивості газу формуються різні математичні моделі, що дають можливість встановлювати певні загальні висновки про характер течій. В багатьох випадках розв'язання відповідних математичних задач пов'язане з великими труднощами і дані про конкретні випадки обтікання тіл одержують з допомогою експерименту, часто досить складного і дорогого. Розвиток комп'ютерної техніки відкрив принципово нові можливості одержання кількісних оцінок характеристик потоків. Сформувався новий розділ механіки — комп'ютерна динаміка рідини та газу[13]
В історичному нарисі відмічено перший результат, який можна віднести до досягнень теоретичної аеродинаміки. Це оцінка Ньютоном сили, що діє на пластинку в потоці. Перші теоретичні результати дозволили сформулювати загальні оцінки про закони пропорційності сили опору і швидкості набігаючого потоку. В сучасній аеродинаміці розроблено велику кількість математичних моделей, призначених для вивчення потоків з різними швидкостями та різними властивостями газу. Такі моделі формуються на базі загальних законів збереження. Однак використання лише законів збереження не дозволяє сформулювати повну систему рівнянь для опису потоку. Крім законів збереження слід використовувати так звані рівняння стану, які описують зв'язок між кінематичними, силовими характеристиками та температурою в газі для певних конкретних умов існування потоку.
Найпростіша модель, що використовується в аеродинаміці — це модель нестисливого ідеального газу. В такому уявному газі відсутні зсувні напруження, в'язкість, теплопровідність. Саме при розгляді цієї найпростішої моделі можна зрозуміти основні моменти в процедурі побудови математичних моделей в механіці суцільного середовища. При цьому приведемо основні рівняння, використовуючи Декартову систему координат, в якій було записано рівняння нерозривності в попередньому розділі. Крім рівняння нерозривності при дослідженні руху частинок середовища слід використати рівняння другого закону Ньютона. При цьому відразу врахуємо припущення про те, що розглядається ідеальний газ (рідина). Такий газ можна визначити, як середовище, в якому вектор зусиль на будь-якій поверхні всередині газу перпендикулярний поверхні і має в даній точці постійну величину при зміні орієнтації площини. В такому середовищі відсутній опір при зсувному русі одного шару газу відносно іншого. Це значить по суті ігнорування в'язкістю газу, яка притаманна кожному реальному газу чи рідині.
Співвідношення другого закону Ньютона запишемо для елементарного об'єму газу в вигляді паралелепіпеда зі сторонами в формі[9].
Тут об'ємна сила та використано традиційне позначення для оператора градієнта скалярної величини тиску . Оскільки рівняння записано відносно конкретної матеріальної частинки то при диференціюванні вектора швидкості слід враховувати залежність від часу координат частинки речовини в векторі швидкості . Тому при записі в координатній формі три рівняння руху частинки середовища матимуть вигляд.
- .
Ці рівняння називаються рівняннями Ейлера. Система рівнянь (1) та (2) при заданих об'ємних силах має чотири рівняння відносно п'яти невідомих функцій, зумовлює її неповноту (незамкнутість). Саме додатковим рівнянням, що доповнює систему до замкнутої, визначаються фізичні властивості середовища. Тому вони називаються рівняннями стану. Часто ці рівняння мають описувати досить складні процеси, що відбуваються в потоці. Для розуміння певних найпростіших явищ, пов'язаних з рухом газу можна використати прості рівняння стану. Таким рівнянням може бути співвідношення, що відображає припущення про те, що в процесі руху рідини її густина залишається сталою величиною (нестислива рідина). Математично це виражається рівнянням
Тепер система рівнянь (1)-(3) є замкнутою і формує основні співвідношення математичної моделі ідеальної нестисливої рідини. Для одержання кількісних характеристик потоку ця система рівнянь має бути розв'язаною при певних початкових та граничних умовах. За такою технологією будуються математичні моделі для різних типів течій в аеродинаміці. Слід мати на увазі, що побудова математичної моделі, адекватної процесу, що досліджується, є найважливішим етапом в вирішенні задач теоретичної та прикладної аеродинаміки. Нелінійність рівнянь руху (2) вказує на джерело суттєвих труднощів в одержанні розв'язків відповідних математичних задач. На цей час існує досить значне число повних математичних моделей для опису аеродинамічних явищ. Найбільшу увагу дослідників потоків з відносно невеликими швидкостями зосереджено на моделях, що включають рівняння Нав'є-Стокса і описують поведінку нестисливого газу чи рідини з урахуванням ефектів в'язкості.
Відсутність загальних розв'язків основних рівнянь аеродинаміки спонукало до розгляду частинних випадків руху рідин та газів. Математичною основою для виділення характерних типів потоків є загальна теорема Гельмгольца[14] про можливість представити довільне векторне поле в вигляді суми безвихрового та соленоїдального полів. Це твердження виражається наступною формулою для довільного вектора :
Вирази для диференціальних операторів та приведено в[14].
Відповідно до такого представлення вектора швидкості течії можуть мати властивості потенціальності, соленоїдальності, або вихоровості.
Для якісного аналізу особливостей таких потоків важливе значення має запис закону збереження енергії в величинах, які входять в загальні рівняння аеродинаміки. Це співвідношення, знане як Закон Бернуллі, має вигляд:
- ,
В загальному випадку постійна величина в правій частині рівняння має різні значення на різних лініях течії (траєкторії, або вихрової лінії). Якщо середовище потенціальне, або вихрові лінії збігаються з лініями течії (гвинтові течії), то ця величина однакова для всіх його точок. Важливо, що це співвідношення справедливе для усталеного руху ідеального баротропного середовища, коли потенціальні об'ємні сили обмежуються силами тяжіння[15][6].
Для нестаціонарного потенціального руху ідеального баротропного середовища в полі потенціальних об'ємних сил буде справедливий інтеграл Коші—Лагранжа. Для нестаціонарного вихрового руху в'язкого нестисливого середовища в полі потенціальних об'ємних сил — узагальнена формула Коші—Лагранжа[16].
Тут приведені співвідношення однієї з найпростіших математичних моделей в аеродинаміці. При необхідності врахувати в'язкість газу використовують рівняння Нав'є-Стокса з відповідними граничними умовами. Розв'язки граничних задач здатні описати такі важливі фізичні явища при обтіканні тіл як відрив потоку та формування примежового шару. В задачах газової динаміки, тобто при дослідженні трансзвукових рухів, також часто використовується модель ідеального газу, Однак, в таких рухах газу важливо враховувати крім стисливості і теплові ефекти. Рівняння стають набагато складнішими, ніж приведені вище і в зв'язку з наявністю в потоці поверхонь розриву в значеннях визначальних параметрів, формулюються для окремих підобластей потоку. Крім того, задачі суттєво ускладнюються в зв'язку з наявністю в потоці ударних хвиль[17] Теоретичні дослідження з використанням різних моделей середовища, хоч і не можуть враховувати ряд факторів, відіграють велику роль в процесі обробки та інтерпретації результатів експерименту.
Історично практична робота по використанню людиною аеродинамічних сил почалася набагато раніше ніж були сформовані певні загальні уявлення про особливості взаємодії тіл з потоками. Перш за все слід вказати на використання вітрових рушіїв — вітряків. Перші документальні свідчення відносно їх використання походять з Персії і відносяться до 7 століття до нашої ери. Характерно, що це були вітряки з вертикальною віссю обертання. Історія традиційних для європейського пейзажу вітряків починається з 12 століття[18] Величезний практичний досвід накопичено людством по використанню енергії вітру з допомогою вітрила. Перші вказівки на використання вітрильних човнів знаходять на зображеннях трипільської кераміки. що датуються 6-5 тисячоліттям до нашої ери[19].
Аеродинаміка вітряків та вітрил залишається актуальним розділом аеродинаміки і в наш час. Особливо важливі результати одержані в аеродинаміці при проведенні цілеспрямованого експерименту з використанням накопичених теоретичних знань про закономірності формування потоків в різних умовах. Розвиток експериментальної аеродинаміки базувався на прогресі в створенні пристроїв для генерації потоків з потрібними властивостями — аеродинамічних труб та розробці достатньо точних і надійних засобів вимірювання характеристик потоків. Велике значення для розвитку експериментальної аеродинаміки мають сучасні методи комп'ютерної реєстрації та обробки результатів вимірювань. Основною метою аеродинамічного експерименту є визначення структури і характеристик газу навколо тіла а також визначення силових, теплових, акустичних факторів взаємодії потоку з тілом.
Сучасні аеродинамічні труби являють собою надзвичайно складний інженерний комплекс, що забезпечує створення потоку з відповідними характеристиками та надійну реєстрацію характеристик потоку та інтегральних силових факторів. На рисунку приведено зображення однієї із таких труб. В Україні експериментальні комплекси, що включають аеродинамічні труби, створено в Харківському національному авіаційному університеті, київському національному авіаційному університеті та в Авіаційному науково-технічному комплексі Антонов.
Оскільки в більшості випадків експерименти проводяться на моделях важливим є питання встановлення відповідності між модельним експериментом та поведінкою реального об'єкту. Питання коректного моделювання є предметом спеціальної теорії подібності[20]. Досить повний перелік конкретних проблем, що виникають при проведені експериментальних досліджень в аеродинаміці представлено в лекційному курсі одного із американських університетів https://web.archive.org/web/20150411121326/http://www.ltas-aea.ulg.ac.be/cms/index.php?page=experimental-aerodynamics-course.

Для підвищення ефективності експериментальних досліджень в аеродинаміці велике значення мало створення таких новітніх засобів вимірювання, як лазерний доплерівський вимірювач швидкості та оптичного методу візуалізації потоку (Particle image velocimetry).
Техніка проведення аеродинамічного експерименту постійно вдосконалюється. Для обміну досвідом між багатьма лабораторіями видається спеціалізований науковий журнал Experiments in Fluds. Повний виклад основних складових методики проведення аеродинамічного експерименту приведено в[21]
Комп'ютерна аеродинаміка це специфічний розділ аеродинаміки. Для дослідження характеристик потоків в комп'ютерній аеродинаміці використовуються математичні моделі, які формуються в рамках підходів теоретичної аеродинаміки. Але методи розв'язання відповідних початково-граничних задач досить специфічні. Відмова від використання методів аналізу, що базується на асимптотичних співвідношеннях нескінченно малих величин, практично приводить до формування нового розділу математики — дискретної математики[22] Використання методів дискретного аналізу відкрило принципові можливості для одержання кількісних оцінок характеристик потоків, які неможливо одержати в рамках існуючих аналітичних підходів. Широке використання чисельних методів в механіці суцільних середовищ привело до формування нової гілки аерогідромеханіки, яку можна визначити, як комп'ютерна механіка плину (Computer Fluid Dynamics — CFD). Накопичений досвід використання методів, пов'язаних з заміною похідної скінченною різницею, висвітлив дві головні проблеми. Перш за все стала зрозумілою необхідність дуже уважних підходів до організації обчислювального процесу, необхідності узгодження величини скінченних кроків по просторовим координатам та часу[23] Виникають певні питання при проведенні обчислень на великих часових інтервалах. Тому зараз розробляються спеціальні стандарти, що регламентують обчислювальній процес для забезпечення надійності і достовірності одержаних результатів[24], З іншого боку результати чисельних розв'язків розкрили глибинну сутність складності відповідних математичних задач, зумовлену величезною складністю фізичних процесів, що реалізуються в потоках газів та рідин. Ці результати привели к формуванню нових понять(детермінований хаос, дивні атрактори, фрактали). які стали могутнім засобом пізнання практично в усіх галузях сучасної науки.
Комп'ютерний експеримент з використанням сучасної техніки стає не лише помічником в процесі вирішення інженерних проблем аеродинаміки, а здатен замінити дуже дорогі фізичні експерименти в аеродинамічних трубах. Згідно з даними відомої комп'ютерної фірми Крей (Cray), яка забезпечувала обчислення для фірми Боїнг, чисельне моделювання широко використовувалося при розробці літака Боїнг 787. За їх даними при проєктуванні попередньої моделі Боїнг 767 було проведено 77 широкомасштабних експериментів в аеродинамічних трубах. При створенні Боїнг 787 їх здійснено всього 11. Така різниця зумовлена дуже широким використанням чисельного експерименту. Проведення обчислень на суперкомп'ютерах зайняло 800 000 процесорних годин (http://investors.cray.com/phoenix.zhtml?c=98390&p=irol-newsArticle&ID=1022899 [Архівовано 17 травня 2019 у Wayback Machine.]). На рисунку для частинного випадку двовимірної задачі показано вигляд області інтегрування та типову сітку, що використовується при заміні похідних скінченними різницями.

Для забезпечення необхідної точності оцінок аеродинамічних характеристик сітка має згущатися в областях з відносно різкої зміни структури потоку.
Серед значної кількості різних програмних продуктів, що використовуються для одержання кількісних характеристик потоків великою популярністю користується універсальна комерційна система система ANSYS. Сучасні інформаційні технології дають можливість для оперативного обговорення проблем, пов'язаних з практичним використанням системи. Великою популярністю серед програмістів користується форум користувачів http://www.cfd-online.com/Forums/ansys/ [Архівовано 19 березня 2015 у Wayback Machine.].
Літак це складна інженерна конструкція, призначена для виконання різного роду транспортних робіт шляхом здійснення польотів в атмосфері. Складність конструкції, складність системи керування цією конструкцією в процесі польоту зумовлені особливостями формування сил та їх моментів на різних етапах польоту, зміною властивостей атмосфери, взаємодією конструкції з силовою установкою, особливостями системи керування. Оцінка ролі вказаних факторів та напрацювання відповідних рекомендацій до правил експлуатації літака виконуються, як правило, для кожної конкретної моделі літака окремо і є дуже важливою частиною роботи авіаційних конструкторських бюро. Як приклад, що ілюструє характер і зміст такої роботи можна вказати на книгу, що описує аеродинаміку популярного літака АН-24[25]. Розуміння фізичних основ польоту літаків формується при вивченні таких розділів аеродинаміки, як аеродинаміка крилового профіля та аеродинаміка крила .
Закономірності формування потоків повітря та їх взаємодії з рухомими об'єктами мають широке застосування при вирішенні широкого кола прикладних проблем. Звичайно, проблеми створення та використання ефективних літальних апаратів мають особливе значення і тут вирішення аеродинамічних задач має вирішальне значення. У зв'язку з цим такі розділи як аеродинаміка крила слід винести в окрему статтю. Для ілюстрації використання аеродинамічних закономірностей тут коротко розглянемо наступні теми:
Газодинаміка турбін та компресорів
[ред. | ред. код]Загальна властивість потоків повітря генерувати при обтіканні тіл специфічної форми складові аеродинамічних сил, перпендикулярних до напрямку потоку, широко використовується при створенні таких інженерних конструкцій як турбіни та певної конструкції компресори. В них на основі вказаного явища організується перетворення кінетичної енергії потоку в енергію обертального руху. Робочим тілом в них може бути водяна пара, гази, що утворюються при спалюванні різних палив, та вода. В усіх випадках для створення обертального моменту використовуються закономірності обтікання елементів типу крилових профілів в авіації. Саме на таких елементах при взаємодії їх з потоком виникають складові сил, перпендикулярні до напрямку потоку. Основні дані про принципи роботи турбін надано в[26]
Завдяки засобам масової інформації громадськість багато разів на рік має можливість спостерігати величезну руйнівну силу таких аеродинамічних явищ, як потужний вітер, торнадо, ураган. Сили, що виникають при взаємодії інтенсивних потоків повітря здатні завдати великої шкоди довкіллю, зруйнувати будинки та інші споруди. Найвідомішою подією в історії спостережень за взаємодією потоків повітря з інженерними спорудами було руйнування Такомського мосту в 1940 році в США. При швидкості вітру 18 м/с в центральному прольоті мосту виникли коливання з великою амплітудою, що врешті-решт і призвело до руйнування. Ця подія справила значний вплив на розвиток досліджень в галузі аеродинаміки конструкцій та визначенні механізмів передачі енергії потоку в енергію коливальних рухів. В авіації подібне явище відоме під назвою флатер.[27] Значний діапазон зміни форм споруд, їх взаємного розташування та зростання висоти будівель стимулюють розвиток аеродинамічних досліджень в інтересах будівництва. При цьому йдеться не лише про визначення сил, що можуть виникати під дією вітру на окрему споруду. Об'єктом досліджень є цілі мікрорайони великих міст. Рекомендації будівельникам, що ґрунтуються на аеродинамічних дослідженнях, мають забезпечити певний рівень комфорту мешканцям та надійність експлуатації споруд.[28].
Вивчення властивостей потоків при обтіканні швидкісних автомобілів має дати основу для вирішення ряду інженерних проблем. Перш за все йдеться про зменшення аеродинамічного опору. Практично всі нові моделі автомобілів проходять прискіпливе тестування а аеродинамічних трубах. Оскільки закони аеродинаміки обійти неможливо форма автомобілів різних марок практично подібна[29]. Не менш важливим є питання про зменшення шуму при русі автомобіля, що важливо, як для навколишнього середовища, так і для пасажирів автомобіля http://magazine.autotechnic.su/technology/aero/aero.html [Архівовано 2 жовтня 2014 у Wayback Machine.].
Для вирішення аеродинамічних проблем автомобілебудівники створюють великі і дуже дорогі експериментальні лабораторії. Наприклад, лабораторія фірми DiamlerChraysler коштувала більше 37 мільйонів доларів. В ній експериментально вирішувалися питання підвищення ефективності використання пального (зменшення лобового опору), мінімізації вітрового шуму та оцінки надійності зовнішніх елементів автомобіля.
Результати досліджень в аеродинаміці мають важливе застосування не лише в авіації та наземному транспорті. Зараз важко вказати вид спорту, в якому б підвищення результатів не було б пов'язано з досягненнями аеродинаміки. Широко відомі факти польоту футбольного м'яча по криволінійній траєкторії можна зрозуміти лише на основі аеродинамічних досліджень. Такі дослідження можуть також надати рекомендації відносно методів керування характеристиками такого польоту.
Аеродинаміка спортивних м'ячів є важливою областю прикладної механіки. У відповідь на запит з цього питання одна з наукових баз даних пропонує більш ніж півтори тисячі наукових статей. Дослідження, переважно, проводяться в аеродинамічних трубах в широкому діапазоні швидкостей потоку. Перш за все в них з'ясовується вплив на аеродинамічні характеристики різних відхилень від форми ідеальної сфери. Дослідження футбольного м'яча, наприклад, пов'язані з вивченням впливу змін в технології його виготовлення на аеродинамічні характеристики. Так, до 1970 року оболонка м'яча формувалася з 17 шматків шкіри. Потім почали використовувати синтетичні матеріали і кількість частин зменшилася до 14. Вплив таких змін детально досліджується в[30]. Автори дослідили також м'яч з оболонкою, сформованою з 32 фрагментів. Було встановлено залежність опору від швидкості польоту та певне зростання опору м'яча з 32 фрагментами оболонки. Для всього діапазону швидкостей польоту м'яча до швидкості 90 км/год опір виявився меншим, ніж опір ідеальної сфери. Дуже цікавою є аеродинаміка м'яча для гольфу, в якого «навмисне» формуються відхилення від сферичної форми. Широке висвітлення проблем аеродинаміки м'ячів для різних спортивних ігор представлено в огляді[31]
Особливий інтерес до питань аеродинаміки виявляється в зв'язку з розвитком професійного велоспорту. Глибокий аналіз прикладних наукових задач, що забезпечують зростання результатів в цьому виді спорту представлено в монографії[32]. Серед цих задач чільне місце посідають задачі аеродинаміки. На швидкості близько 50 км/год аеродинамічний опір велосипедиста становить близько 90 % від загального опору рухові. Саме боротьба за кожен відсоток зниження опору зумовлює і форму шолома, і одяг і конструкцію велосипеда. Останнім часом розглядається можливість відходу від використання круглих трубок в елементах велосипеда. Спостерігаючи за велогонкою майже завжди можна бачити групу гонщиків, які тримаються дуже близько один до одного. Результати комп'ютерного моделювання руху такої групи показують, що при відстані між гонщиками в 10 см в групі з 6-8 осіб можливо зниження опору на величину до 30 %[33]
Див. також м'яч для гольфу.
Величезна кількість комах (~ видів) в процесі еволюції розвинула здатність літати.[34] При цьому вони застосовують складні екзотичні механізми для утворення нестаціонарних ефектів, що забезпечують надзвичайно високі аеродинамічні характеристики та маневреність польоту. Наприклад, швидкість польоту деяких бабок може сягати 25 м/с, прискорення — 130 м/с2, сумарна сила тяги може в 13 раз перевершувати вагу тіла, а розвернутись на 180° бабка може за три махові цикли. Спостереження за польотом комах стимулювало інтерес до питань аеродинаміки польоту як аеродинаміків, так і біологів. Було з'ясовано, що крила комах махають при числах Маха , числах Рейнольдса , та числах Струхаля [35] При цьому частота махів крил може досягати 1000 Гц. Вивчення аеродинаміки комах дає базу для створення літаючих мікророботів.[36]

З точки зору аеродинаміки маємо начебто таку ж ситуацію як і з літаком — здатність літати у живої істоти, що важча за повітря. Проте на відміну від стаціонарної циркуляційної сили Жуковського, яка утворюється на крилах літаків, природа сил, що виникають на крилах комах є, як правило, інерційно-вихрова[37] і принципово нестаціонарна, через що внесок миттєвих приєднаних мас домінує.[38] З усіх кромок крил сходять вихрові шари, які уздовж передніх кромок утворюють вихрові структури, приєднані до них при морфологічному маху вниз (фазі пронації).[39] Завдяки цим вихорам над крилами утворюються зони пониженого тиску, які спричиняють збільшення корисних навантажень. Після цього крила миттєво розвертаються (фаза супинації) і здійснюють морфологічний мах уверх під малими кутами атаки, потім знов розвертаються і все повторюється заново. Однак у 1973 році Вейс-Фо відкрив складніший механізм «хлопок-та-ривок», який застосовують деякі маленькі комахи при нормальному тріпотливому польоті (зависанні). Оскільки у фазі «хлопку» передні, а у фазі «ривку» — задні кромки крил наближені одна до одної, це призводить до утворення інтенсивніших вихорів при морфологічному маху вниз та створює ефект реактивного струменя наприкінці циклу.[40]
Значну роль у вивченні особливостей польоту комах відіграє комп'ютерне моделювання.[34][41][42][43][44][45][46][47][48] Проте побудова достовірних теоретичних моделей махів крил комах неможлива без знання точної тривимірної кінематики руху їх точок.[49][38][50] Першими були спроби застосування однієї високошвидкісної телекамери для експериментів з прив'язаними комахами в аеродинамічній трубі[51], потім — для експериментів з комахами у вільному польоті[52] і тільки останнім часом з'явилась можливість застосування одночасно трьох високошвидкісних цифрових відеокамер зі швидкістю 5000 кадрів на секунду.[53][54] Побудовані також роботизовані динамічно масштабовані моделі крил комах.[55][56][39][57][58][59] Це дозволяє обійти декілька складних експериментальних проблем: урахування внеску сил інерції крил, синхронізація кінематики та навантажень на крилах, достовірність, точність вимірювань, тощо, однак має головний недолік — штучність та спрощеність законів руху крил. Незважаючи на велику кількість лабораторних досліджень та розрахунків в рамках різних математичних моделей, низка питань аеродинаміки комах залишаються дискусійними.[60][61][62]
- Аеродинаміка [Архівовано 20 грудня 2016 у Wayback Machine.] // Українська радянська енциклопедія : у 12 т. / гол. ред. М. П. Бажан ; редкол.: О. К. Антонов та ін. — 2-ге вид. — К. : Головна редакція УРЕ, 1974–1985.
- Аеродинаміка [Архівовано 20 грудня 2016 у Wayback Machine.] // Енциклопедія сучасної України / ред. кол.: І. М. Дзюба [та ін.] ; НАН України, НТШ. — К. : Інститут енциклопедичних досліджень НАН України, 2001–2024. — ISBN 966-02-2074-X.
- Аерогідрогазодинаміка: підручник / В. Г. Лебедь, Ю. І. Миргород, Є. О. Українець. — Х. : ХУПС ім. Івана Кожедуба, 2011. — 415 с.
- Аеродинаміка / Н. І. Ахієзер, В. І. Путята. — Харків ; Київ: ОНТВУ «Транспорт і зв'язок» , 1932. — 148 с.[63]
- Аеродинаміка вентиляції: навч. посіб. для студ. вищих навч. закл. / С. С. Жуковський, В. Й. Лабай ; Національний ун-т «Львівська політехніка». — Л. : Видавництво Національного університету «Львівська політехніка», 2003. — 370 с.: рис., табл. — Бібліогр.: с. 365—370. — ISBN 966-553-303-7
- Аеродинаміка вентиляції: навч. посіб. для студентів спец. 7.06010107 «Теплогазопостачання і вентиляція» / Довгалюк В. Б. — Вид. 2-ге, випр. і допов. — Київ: Укргеліотех, 2015. — 365 с. : рис., табл. — Бібліогр.: с. 357—359. — 300 экз. — ISBN 978-966-97475-4-9
- Аеродинаміка літальних апаратів / Харків: ХУПС ім. Івана Кожедуба, 2015.[64]
- Аеродинаміка літальних апаратів: підруч. для студ. вищ. навч. закл. I—II рівнів акредитації, що навч. за спец. «Виробництво авіаційних та ракетно-космічних апаратів», «Виробництво авійційних літальних апаратів» / Г. Н. Котельніков [та ін.] ; ред. Ю. М. Терещенко. — К. : Вища освіта, 2002. — 254 с.: рис. — ISBN 966-95995-9-8
- Аеродинаміка і динаміка польоту вертольота: підручник / Харк. ун-т Повітр. Сил ім. І. Кожедуба. — Х. : ХУПС, [200?].
- Ч. 2 : Динаміка польоту вертольота / А. Г. Зінченко [та ін.] ; за заг. ред. канд. техн. наук, доц. В. М. Костенка та канд. техн. наук, доц. І. Б. Ковтонюка. — 2010. — 268 с. : рис. — Бібліогр.: с. 262. — 60 пр. — ISBN 978-966-468-052-0
- Ахієзер Н. Аеродинамічні досліди. К., 1924.
- Гідро- та аеродинаміка полютантів: навч. посіб. для студ. вищих навч. закл. / Б. М. Лижичка ; Інститут менеджменту та економіки «Галицька академія». — 2. вид., доп. і перероб. — Івано-Франківськ: ІМЕ «Галицька академія», 2005. — 196 с.: рис., табл. — Бібліогр.: с. 191—192. — ISBN 966-7768-54-6
- Динаміка польоту літальних апаратів: навч. посіб. / О. Г. Войтенко, І. Б. Ковтонюк, В. М. Костенко, Ю. І. Миргород, Д. М. Обідін, І. Ю. Тригуб. — Х.: ХУПС, 2005. — 173 с.
- Основи аеродинаміки і тепломасообміну: Навч. посібник / Озарків І. М., Сорока Л. Я., Грицюк Ю. І. — К.: ІЗМН, 1997. — 280 с.
- Аэрогидродинамика и аэроакустика: проблемы и перспективы. Сборник научных трудов. ХАИ. — Харьков, ХАИ, 2009.
- Аэродинамика и динамика полета транспортных летательных аппаратов / под ред. проф. Касторского В. Е. — Рига: Риж. институт инженеров гражд. авиации.
- Кн. 1 : Аэродинамика / Гаухман Я. Н., Касторский В. Е., Логачев Ю. Г., Стадник И. В. — 1968. — 457 с. : черт. — Библиогр.: с. 406 (17 назв.).
- Кн. 2 : Динамика полета / Баранов А. А., Сорокин Э. И., Тотиашвили Л. Г. — 1970. — 623 с. : черт. — Библиогр.: с. 532 (12 назв.).
- Аэродинамика магистральных автопоездов /А. Н. Евграфов, М. С. Высоцкий, А. И. Титович. — Минск: Наука и техника, 1988. — 232 с.
- Аэродинамика колесного транспорта /А. Н. Евграфов, М. С. Высоцкий. — Минск: Белавтотракторостроение, 2001. — 368 с.
- Аэродинамика: проблемы и перспективы. Сб. научных трудов. Вып. 2. — Харьков: ХАИ, 2006.
- Вопросы эксплуатационной аэродинамики: сб. науч. тр. / Киев. ин-т инженеров гражд. авиации ; [отв. ред. А. М. Мхитарян]. — Киев: КИИГА, 1989. — 132 с. : ил.
- Ищенко С. А., Трюхан О. Н. Принципы полета. — Киев: НАУ, 2011. — 420 с.
- Ищенко С. А., Трюхан О. Н. Принципы полета (альбом графиков, схем, таблиц по курсу дисциплины). — Киев: НАУ, 2010. — 100 с.
- Механика жидкости и газа. Конспект лекций / Иванов К. Ф. , Сурков С. В. — Одесса: ОГПУ, 1995. — 124 стр.
- Моделирование полета и аэродинамические исследования: Сб. научн. тр. — К.: КИИГА, 1988.
- Молекулярная газовая динамика и ее приложения в ракетно-космической технике / В. П. Басс ; Нац. акад. наук Украины, Нац. косм. агентство Украины, Ин-т техн. механики. — Киев: Наук. думка, 2008. — 269 с. : ил. ; 22 см — Библиогр.: с. 250—265. — ISBN 978-966-00-0746-8
- Основы аэродинамики и динамики полета: учеб. пособие для вузов / В. Е. Касторский ; Ин-т транспорта и связи. — Рига: РКИИГА; Колос, 2010. — 105 с.
- Основы аэрогидрогазодинамики: учебник / В. Ф. Дерягин ; Кировоград. лет. акад. Нац. авиац. ун-та. — Изд. 2-е, перераб. и доп. — Кировоград: Изд-во КЛА НАУ, 2012. — 199 с. : ил., табл., портр.
- Прикладная аэродинамика: сб. научн. тр. — К.: КМУГА, 1997.
- Расчет аэродинамических, летно-технических и маневренных характеристик самолета / Под ред. В. Г. Лебедя, А. П. Романца. — Х.: ХВВАИУ, 1989. — 187 с.
- Теоретические основы аэродинамики: конспект лекций / А. Г. Баскакова [и др] ; Киевский международный ун-т гражданской авиации. — К. : [б.и.], 1997. — 166 с.
- Энергетическая эффективность автомобиля/ Гащук П. Н. — Львов: Свит, 1992. — 208 с. — ISBN 5-11-000626-1
- E. L. Houghton, P. W. Carpenter, Steven Collicott, Daniel Valentine. Aerodynamics for Engineering Students. 7th Edition. Butterworth-Heinemann, 2016. ISBN 9780081001943.[65]
- Anderson, John D. Fundamentals of Aerodynamics. 3rd ed. New York, NY: McGraw-Hill, 2001. ISBN 007237350.[66]
- Bertin, John J. Aerodynamics for Engineers. 4th ed. Upper Saddle River, NJ: Prentice Hall, 2001. ISBN 0130646334.
- Kuethe, Arnold, and Chuen-Yen Chow. Foundation of Aerodynamics. 5th ed. New York, NY: John Wiley and Sons, 1997. ISBN 0471129194.
- Moran, Jack. An Introduction to Theoretical and Computational Aerodynamics. 1st ed. New York, NY: John Wiley and Sons, 2003. ISBN 0486428796.
- Аеродинаміка [Архівовано 17 лютого 2022 у Wayback Machine.] // ВУЕ
- ↑ а б Теодор фон Карман, Аэродинамика. Избранные темы в их историческом развитии. — Москва-Ижевск, НИЦ «Регулярная и хаотическая динамика», 2001. — 208 с. ISBN 5-93972-094-3
- ↑ McLean D. Understanding Aerodynamics: Arguing from the Real Physics. — Wiley,2012. — 576 p. ISBN 978-1-119-96751-4
- ↑ Aerodynamics Index [Архівовано 12 вересня 2009 у Wayback Machine.] (англ.) на сайті NASA.
- ↑ Кривоносов Ю. И. Партийное дело о портрете и приоритете: как власти придержащие заставляли «летать» самолет А. Ф. Можайского. В кн. Легенды и мифы отечественной авиации. — Москва, Фонд содействия авиации «Русские витязи», 2009. — С.7-32.
- ↑ Anderson J. D. A History of Aerodynamics, Cambridge University Press, 1997. — 479 p. ISBN 0-521-66955-3
- ↑ а б Лойцянский Л. Г. Механика жидкости и газа. — М.-Л., Гостехиздат, 1950. — 676 с.
- ↑ В. В. Гончаренко Как люди научились летать.—Киев: Веселка,1986.—335 с.
- ↑ Мандельштам Л. И. Лекции по теории колебаний.. — М.: Наука, 1972. — 470 с.
- ↑ а б Седов Л. И. Механика сплошной среды, т. 1. — М.: Наука, 1970. — 492 с.
- ↑ Басс В. П. Молекулярная газовая динамика и ее приложения в ракетно-космической технике. — К.: Наукова думка, 2008. — 272 с. ISBN 978-966-00-0746-8
- ↑ Ван-Дфйк М. Альбом течений жидкости и газа. --Москва, Мир,1986.--184 с.
- ↑ Samimy M., Breuer K.S., Leal L. G., Steen P. H. A Galery of Fluid Motion. — Cambridge University Press, 2003. — 118 p. ISBN 978-0-521-82773-7
- ↑ Приходько А. А. Компьютерные технологии в аэродинамике и тепломассообмене. — К.: Наукова Думка,2003. — 379 с. ISBN 966-00-0047-2
- ↑ а б Кочин Н. Е. Векторное исчисление и начала тензорного анализа. — М.: Наука,1965. — 427 с.
- ↑ Милн-Томсон Л. М. Теоретическая гидродинамика.--Москва, Мир, 1964.--655с.
- ↑ Shekhovtsov A. V. A Method for Evaluation of an Unsteady Pressure Field in a Mixed Potential-Vortical Domain Adjacent to the Rotating Wing, International Journal of Fluid Mechanics Research, Vol.29, issue 1, 2002, pp.111--123. DOI: 10.1615/InterJFluidMechRes.v29.i1.70
- ↑ Крайко А. Н. Теоретическая газовая динамика: классика и современность. М.: ТОРУПРЕСС,2010. — 430 с. ISBN 978-5-94588-076-4.
- ↑ Tabak J. Wind and Water.--New York, Facts and File,2009. — 208 p. ISBN 978-0-8160-7087-9.
- ↑ Мария Гимбутас Цивилизация великой богиги: мир древней Европы.- М.: РОССПЕН,2006. — 572 с. ISBN 5-8243-0600-1.
- ↑ Седов Л. И. Методы подобия и размерности в механике. — М.: Наука, 1977. — 449 с.
- ↑ Мартынов А. К.Экспериментальная аэродинамика. — Москва, Изд-во оборонной промышленности, 1950. — 478 с.
- ↑ Кемени Дж.,Снелл Дж., Томпсон Дж. Введение в конечную математику. — М.: Мир,1965. — 484 с.
- ↑ Флетчер К. Вычислительные методы в динамике жидкости. — М.: Мир, 1991. — 504 с. ISBN 5-03-001881-6.
- ↑ Standard for Verification and Validation in Computational Fluid Dynamics and Heat Transfer, v.v.20, ASME, 2009, ISBN 9780791832097
- ↑ Л. Е. Богославский Практическая аэродинамика самолета АН-24. — Москва, «Транспорт», 1972. — 200 с.
- ↑ Енергетика. Історія, сучасність та майбутнє. Книга 3. Розвиток теплоенергетики та гідроенергетики. http://energetika.in.ua/ua/books/book-3/part-1/section-3 [Архівовано 24 травня 2015 у Wayback Machine.]
- ↑ Кузьмина С., Карклэ П. Эолова арфа, самолеты и мосты. Наука и жизнь,№ 5, 2009.
- ↑ Реттер Э. И. Архитектурно-строительная аэродинамика. — М.: Стройиздат, 1984. — 294 с.
- ↑ Ybcho W-H.(Ed.) Aerodynamics of Road Vehicles. From Fluid Mechanics to Vehicle Engineering. Dutterwarth-Heinemann, 1990. — 566 p.
- ↑ Alam F., Chowdhury H.,Vjria H., Fuss F. K. A comparative study of football aerodynamics. Procedia Engineering, vol. 2, issue 2, 2010, p.2443-2448.
- ↑ Mehta R.D. Aerodynamics of Sports Balls, Annual Rev. Fluid Mech., 1985, vol.17, p. 151—189.
- ↑ Wilson D. G. Bicycling Science, Thrid Edition. — Cambridge, Massachusetts, The MIT Press, 2004. — 477 p. ISBN 0-262-73154-1
- ↑ Blocken B., Defraeye T., Koninckx E., Carmeliet J.,Hespel.P. Surprising in cycling aerodynamics. Europhysics News, vol. 44, No 1, 2013, p. 20-23.
- ↑ а б Liu H., Ellington C. P., Kawachi K., Van den Berg C. and Willmott A. P., A computational fluid dynamic study of hawkmoth hovering, J. Exp. Biol., Vol. 201, 1998, pp.461-477.
- ↑ Graham K. Taylor, Robert L. Nudds and Adrian L. R. Thomas, Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency, Nature, Vol. 425, 2003, pp.707-711.
- ↑ Dario Floreano, Jean-Christophe Zufferey, Mandyam V. Srinivasan, Charlie Ellington (Eds.), Flying Insects and Robots, Springer: Heidelberg Dordrecht London New-York, 2009, 315p. DOI 10.1007/978-3-540-89393-6
- ↑ Шеховцов А. В., Инерционно-вихревой принцип генерации усилий на крыльях насекомых, Прикладна гідромеханіка, Т.13, № 4, 2011, С.61-76.
- ↑ а б Sergey Shkarayev, Gunjan Maniar, and Alexander V. Shekhovtsov, Experimental and Computational Modeling of the Kinematics and Aerodynamics of Flapping Wing, Journal of Aircraft, Vol.50, No. 6, 2013, pp.1734-1747. DOI: 10.2514/1.C032053
- ↑ а б Charles pp. Ellington, Coen van den Berg, Alexander pp. Willmott and Adrian L. R. Thomas, Leading-edge vortices in insect flight, Nature, Vol. 384, 1996, pp.626-630. DOI:10.1038/384626a0
- ↑ Weis-Fogh, T., Quick estimates of flight fitness in hovering animals, including novel mechanisms for lift production, J. Exp. Biol., Vol. 59, 1973, pp.169-230.
- ↑ Liu H. and Kawachi K., A numerical study of insect flight, J. Comput. Physics., Vol. 146, 1998, pp.124-156.
- ↑ Wang Z. J., Birch J. M., and Dickinson M. H., Unsteady Forces and Flows in Low Reynolds Number Hovering Flight: Two-dimensional Computations vs Robotic Wing Experiments, J. Exp. Biol., Vol. 207, 2004, pp.449-460. doi:10.1242/jeb.00739
- ↑ Ramamurti R., and Sandberg W., A Three-dimensional Computational Study of the Aerodynamic Mechanisms of Insect Flight, J. Exp. Biol., Vol. 205, 2002, pp.1507-1518.
- ↑ Sun M., and Tang J., Unsteady Aerodynamic Force Generation by a Model Fruit Fly Wing in Flapping Motion, J. Exp. Biol., Vol. 205, Jan. 2002, pp.55-70.
- ↑ Sun M., and Tang J., Lift and Power Requirements of Hovering Flight in Drosophila virilis, J. Exp. Biol., Vol. 205, Aug. 2002, pp.2413-2427.
- ↑ Mao Sun, and Shi Long Lan, A computational study of the aerodynamic forces and power requirements of dragonfly (Aeschna juncea) hovering, J. Exp. Biol., Vol. 207, 2004, pp.1887-1901. doi:10.1242/jeb.00969
- ↑ Hiroto Nagai, Koji Isogai, Tatsumi Fujimoto, and Toshiyuki Hayase, Experimental and Numerical Study of Forward Flight Aerodynamics of Insect Flapping Wing, AIAA Journal, Vol. 47, No. 3, 2009, pp.730-742. DOI: 10.2514/1.39462
- ↑ Довгий С. А., Шеховцов А. В., Апробация УМДВ для класса задач о колебаниях крыла в вязкой среде с ограниченным решением на кромках, Вісник Харківського нац. університету, № 863, Сер. «Математичне моделювання. Інформаційні технології. Автоматизовані системи управління», Вип. 12, 2009, С.111-128.
- ↑ Шеховцов А. В., Юнге М., Нахтигаль В., Аэродинамика работы крыльев пчел в режиме вентилирования, Прикладна гідромеханіка, Т.1, № 4, 1999, С.83-86.
- ↑ Roland Liebe (Ed.), Flow Phenomena in Nature: A challenge to engineering design, WIT Press: Southampton, Billerica, 2007, 372p.
- ↑ Jensen M., Biology and physics of locust flight. iii. The aerodynamics of locust flight, Proc. R. Soc. B., Vol. 239, 1956, pp.511-552.
- ↑ Ellington, C. P., The aerodynamics of hovering insect flight. III. Kinematics, Phil. Trans. R. Soc. Lond. B, Vol. 305, 1984, pp.41-78.
- ↑ Steven N. Fry, Rosalyn Sayaman, Michael H. Dickinson, The aerodynamics of free-flight manuevers in Drosophila, Science, Vol.300, 2003, pp.495-498.
- ↑ Lingxiao Zheng, Xiaolin Wang, Afzal Khan, R.R.Vallance, Rajat Mittal and Tyson L. Hedrick, A Combined Experimental-Numerical Study of the Role of Wing Flexibility in Insect Flight, AIAA-2009-382, 47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition 5—8 January 2009, Orlando, Florida.
- ↑ Maxworthy, T., Experiments on the Weis-Fogh mechanism of lift generation by insects in hovering flight. Part 1. Dynamics of the ‘fling’ , J. Fluid Mech., Vol. 93, 1979, pp.47-63. DOI: https://doi.org/10.1017/S0022112079001774
- ↑ Dickinson M. H. and Götz K. G., Unsteady aerodynamic performance of model wings at low Reynolds numbers, J. Exp. Biol., Vol. 174, 1993, pp.45-64.
- ↑ Michael H. Dickinson, Fritz-Olaf Lehmann, Sanjay P. Sane, Wing Rotation and the Aerodynamic Basis of Insect Flight, Science, Vol.284, 1999, pp.1954-1960. doi:10.1126/science.284.5422.1954
- ↑ Maybury, W. J., and Lehmann, F.-O., The Fluid Dynamics of Flight Control by Kinematic Phase Lag Variation between Two Robotic Insect Wings, J. Exp. Biol., Vol.207, 2004, pp.4707-4726. doi:10.1242/jeb.01319
- ↑ Christopher DiLeo and Xinyan Deng, Design of and Experiments on a Dragonfly-Inspired Robot, Advanced Robotics, Vol.23, issue 7-8, 2009, pp.1003-1021. DOI:10.1163/156855309X443160
- ↑ Sane S.P., The Aerodynamics of Insect Flight, J. Exp. Biol, Vol.206, 2003, pp.4191-4208. DOI:10.1242/jeb.00663
- ↑ Lehmann F-O., The Mechanisms of Lift Enhancement in Insect Flight, Naturwissenschaften, Vol. 91, 2004, pp.101-122. DOI 10.1007/s00114-004-0502-3
- ↑ Wang Z. J., Dissecting Insect Flight, Annu. Rev. Fluid Mech., Vol. 37, 2005, pp.183-210. DOI: 10.1146/annurev.fluid.36.050802.121940
- ↑ Короткий опис видання. Архів оригіналу за 20 грудня 2016. Процитовано 13 грудня 2016.
- ↑ Коротко про видання на сторінці Кафедри аеродинаміки та динаміки польоту ХУПС ім. Івана Кожедуба. Архів оригіналу за 20 грудня 2016. Процитовано 13 грудня 2016.
- ↑ Коротко про видання на сайті elsevier.com. Архів оригіналу за 20 грудня 2016. Процитовано 13 грудня 2016.
- ↑ Коротко про видання на сайті abebooks.com. Архів оригіналу за 20 грудня 2016. Процитовано 13 грудня 2016.































