Спір Ньютона і Лейбніца про пріоритет

Статуї І. Ньютона й Г. В. Лейбніца у дворі Оксфордського музею природничої історії

Спір Ньюто́на й Ле́йбніца про пріорите́т (англ. Leibniz–Newton calculus controversy, нім. Prioritätsstreit) — суперечка про пріоритет відкриття диференціального й інтегрального числення між Ісааком Ньютоном (1642—1727) і Готфрідом Вільгельмом Лейбніцом (1646—1716). Свою версію теорії Ньютон створив ще в 1665—1666 роках, проте не публікував її до 1704 року. Незалежно від нього Лейбніц розробив свій варіант диференціального числення (з 1675 року) хоча первісний поштовх, ймовірно, його думка отримала з чуток про те, що таке числення у Ньютона вже є, а також завдяки науковим бесідам в Англії й листуванню з Ньютоном. На відміну від Ньютона, Лейбніц відразу опублікував свою версію і надалі, разом з Якобом і Йоганном Бернуллі, широко пропагував це відкриття по всій Європі. Більшість науковців на континенті не сумнівалися, що аналіз відкрив Лейбніц. Коли Ньютон вирішив опублікувати свої праці на цю тему, виникло питання про пріоритет вчиненого відкриття. Запекла суперечка не завершилася зі смертю Лейбніца й тривала зусиллями прихильників основних учасників, припинившись тільки зі смертю Ньютона.

Полярні точки зору з приводу пріоритету Ньютона або Лейбніца висловлювалися істориками математики аж до початку XX століття. З середини минулого століття істотно зросла кількість відомих джерел, і сучасні дослідники прийшли до висновку про те, що Ньютон і Лейбніц зробили свої відкриття незалежно один від одного. У питанні, чий внесок у виникненні математичного аналізу був вирішальним, історики математики схиляються або до компромісної точки зору про те, що це сталося в результаті роботи багатьох поколінь математиків, або ж визнають вирішальною роль вчителя Ньютона Ісаака Барроу (1630—1677), чиї праці були відомі також Лейбніцу.

Науковий пріоритет у XVII столітті

У XVII столітті, як і зараз, питання наукового пріоритету мало велике значення для вчених. Однак у цей період наукові журнали тільки створювалися, й загальновизнаний механізм фіксації пріоритету шляхом публікації інформації про відкриття ще не сформувався. Серед методів, які використовували вчені, були анаграми, запечатані конверти, розміщені в безпечному місці, листування з іншими вченими або приватне повідомлення. Лист до засновника Французької академії наук Марена Мерсенна для французького вченого або секретаря Лондонського королівського товариства Генрі Ольденбурга практично мав статус опублікованої статті. Першовідкривач, крім здобуття слави, був позбавлений необхідності доводити, що його результат був отриманий не за допомогою плагіату. Крім того, пріоритет міг би мати практичне значення, якби це було пов'язано з винаходом нових технічних пристроїв. Широко поширеною стратегією атаки на пріоритет було оголошення відкриття чи винаходу не великим досягненням, а лише вдосконаленням, використовуючи відомі кожному техніки й, отже, не вимагаючи значної майстерності свого автора.

Ряд гучних суперечок про науковий пріоритет XVII століття — епохи, яку американський історик науки Д. Мелі назвав «золотим віком суперечок про пріоритет у вигляді метання брудом», — пов'язаний з Лейбніцом. Перший із них стався на початку 1673 року, під час його першого візиту в Лондон, коли він у присутності відомого математика Джона Пелла презентував свій метод апроксимації рядів різницями. На зауваження Пелла, що дане відкриття вже зроблено Франсуа Реном (François Regnaud) й опубліковано в 1670 році в Ліоні Габріелем Мутоном, Лейбніц дав відповідь на наступний день. У листі до Ольденбурга він писав, що, переглянувши книгу Мутона, він визнає правоту Пелла, але у своє виправдання може надати свої чорнові записи, в яких присутні нюанси, які не виявлені Рено й Мутоном. Отже, чесність Лейбніца була доведена, однак цей випадок йому пригадували пізніше. У той же приїзд до Лондона Лейбніц виявився в протилежному положенні. 1 лютого 1673 року на засіданні Лондонського королівського товариства він продемонстрував свою лічильну машину. Куратор експериментів суспільства Роберт Гук ретельно досліджував прилад і навіть зняв задню кришку. Через кілька днів за відсутності Лейбніца Гук виступив із критикою машини німецького вченого, заявивши, що він міг би зробити простішу модель. Дізнавшись про це Лейбніц, уже повернувшись до Парижа, у листі до Ольденбурга категорично відкинув претензії Гука й сформулював принципи коректної наукової поведінки: «Ми знаємо, що добропорядні та скромні люди воліють, коли вони додумаються до чого-небудь, що співвідносить зі зробленими кимось іншим відкриттями, приписати свої власні поліпшення й додавання першовідкривачу, з тим, щоб не накликати підозри в інтелектуальній нечесті, і бажання справжньої великодушності має їх переслідувати, замість брехливої ​​спраги нечесної наживи». Як ілюстрацію належної поведінки Лейбніц наводить приклад Ніколя Фабрі де Пейреска та П'єра Ґассенді, які виконали астрономічні спостереження, аналогічні виконаним раніше Галілео Галілеєм і Яном Гевелієм відповідно. Дізнавшись про те, що свої відкриття вони зробили не першими, французькі вчені передали свої дослідження першовідкривачам.

Підхід Ньютона до проблеми пріоритету можна проілюструвати на прикладі відкриття закону обернених квадратів застосовного до динаміки тіл, що рухаються під дією сили тяжіння. На підставі аналізу законів Кеплера й власних обчислень Роберт Гук зробив припущення, що рух у таких умовах має відбуватися на орбітах, подібних до еліптичних. Не маючи можливості строго довести своє твердження, він повідомив про нього Ньютону. Не вступаючи далі в листування з Гуком, Ньютон розв'язув цю задачу, а також обернену до неї. Він довів, що з еліптичності орбіт випливає закон обернених квадратів. Його відкриття було викладено в знаменитій праці «Математичні начала натуральної філософії» без згадування імені Гука. За наполяганням астронома Едмонда Галлея, якому рукопис був переданий для редагування й публікації, у текст була включена фраза про те, що про відповідність першого закону Кеплера законом зворотних квадратів «стверджували незалежно Рен, Гук і Галлей». У листуванні з Галлеєм Ньютон сформулював своє бачення ситуації, що склалася:

Математики, які все відкривають, усе встановлюють і все доводять, повинні задовольнятися роллю сухих обчислювачів і чорноробів. Інший же, який нічого не може довести, а тільки на все претендує й все запам’ятовує та забирає всю славу, як своїх попередників, так і своїх послідовників… Й ось я повинен визнати тепер, що все отримав від нього, а що я сам за все тільки підрахував, довів і виконав всю роботу в’ючної тварини за винаходами цієї великої людини.

Як зауважив В. І. Арнольд, Ньютон, вибираючи між відмовою від публікації своїх відкриттів і постійною боротьбою за пріоритет, вибрав і те, й інше.

Передісторія

Винахід диференціального й інтегрального числень

Диференціальний трикутник Паскаля

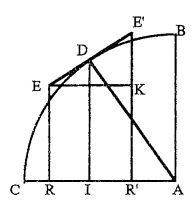
На час Ньютона й Лейбніца європейські математики вже внесли значний вклад у формування ідей математичного аналізу. Розвитком античного «методу вичерпування» для обчислення площ і обсягів займалися голландець Симон Стевін (1548—1620), італієць Лука Валеріо (1553—1618), німець Йоганн Кеплер (1571—1630). Ідеї ​​останнього, мабуть, вплинули — безпосередньо або за посередництвом Галілео Галілея — на розроблений Бонавентурою Кавальєрі (1598—1647) «метод неподільних». Галілей також займався розробленням питання про поняття нескінченно великої й нескінченно малої величин. У 1639 році Кавальєрі отримав найважливіший результат, проінтегрував степеневу функцію. У період між 1636 і 1655 роками практично незалежно один від одного це досягнення повторили у Франції Жиль Роберваль (1602—1675), Блез Паскаль (1623—1662), П'єр Ферма (1601—1665) і в Англії Джон Валліс (1616—1703). 1626 року Грегуар де Сент-Вінсент, розвиваючи «метод вичерпання», прийшов до ідеї вистави кривої як границі, вписаної в багатокутник або описаного навколо багатокутника, однак, оскільки він позиціонував своє досягнення як рішення задачі квадратури кола, воно було проігноровано більшістю сучасних йому математиків; згодом його репутація була відновлена ​​Ньютоном і Лейбніцом. У своїй роботі «Трактат про синус чверті кола» («Traité des sinus du quart de cercle», 1659) Паскаль впритул наблизився до встановлення зв'язку між завданням побудови дотичної до кривої й обчисленням площі під нею. У цій роботі наводиться зображення фігури, яка згодом стала відомою як «диференційний трикутник» і що ілюструє граничний перехід при прагненні збільшень аргументу й функції до нуля. Однак Паскаль, як і в 1624 році Вілеброрд Снеліус (1580—1626), не зробив цього переходу. В опублікованій у 1638 році роботі П'єр Ферма запропонував метод визначення максимумів і мінімумів, що зводиться, в сучасній термінології, до визначення нулів першої похідної. Розв'язуючи задачу пошуку центра ваги параболічного сегмента, Ферма знайшов зв'язок між завданнями з пошуку дотичної й обчислення площі. Попри те, що свої методи Ферма застосовував тільки до раціональних функцій, він ближче всіх наблизився до винаходу математичного аналізу — за винятком, можливо, Ісаака Барроу (1630—1677). Важливе значення мала публікація в 1668 році книги «Logarithmotechnia» Ніколаса Меркатора (1620—1687), в якій було наведено розкладання в ступеневий ряд натурального логарифма («ряд Меркатора») й зазначено його застосування для обчислення площі під гіперболою.

Барроу — учитель Ньютона — у своїх математичних побудовах сильно тяжів до їхньої геометричної інтерпретації. Його метод обчислення дотичних ґрунтувався на результатах континентальних математиків, а також англійців Джеймса Грегорі (1638—1675) й Джона Валліса. Ймовірно, йому також були відомі роботи Ферма з аналізу, видані посмертно в 1679 году. Основна праця Барроу в області аналізу «Lectiones Geometricae» була видана в 1670 році. У 1673 році її придбав Лейбніц, але, за його твердженням, не читав.

Історики математики по-різному оцінюють роль Ньютона й Лейбніца в контексті досягнень їхніх попередників. Згідно з Едмундом Гоппе (1928), можна виділити дві незалежні лінії в історії математичного аналізу — кінематичну, яка веде до Ньютона через Платона, Архімеда, Галілея, Кавальєрі й Барроу, й атомістичну — до Лейбніца через Демокрита, Кеплера, Ферма, Паскаля й Гюйгенса (1629—1695). Точка зору Карла Боєра (1949) полягає в тому, що ці ідеї в середині XVII століття очікували того, що їх хтось систематизує й узагальнить. На думку Маргарет Барон (Margaret E. Baron) (1969), першовідкривачем треба визнати Барроу, а Ньютон і Лейбніц лише алгебраїчно оформили його ідеї.

Ньютон

У листі до Роберта Гука, датованого 15 лютого 1676 року, Ньютон процитував відомий вислів Бернара Шартрського: «Якщо я бачив далі інших, тому що стояв на плечах гігантів». Ілюстрація з рукопису XV століття.

Збереглося досить багато документів, що розповідають історію відкриття Ньютоном диференціального числення, який він назвав методом флюксій (англ. Method of Fluxions) — те, що згодом стало основою сучасного математичного аналізу[ком. 3][./Спір_Ньютона_і_Лейбніца_про_пріоритет#cite_note-22 [ком. 3]]. У блокноті Ньютона за 1699 рік він пише про те, що, проаналізувавши свої старі записи про витрати, він згадав, що незадовго до Різдва 1664 року він придбав важливі математичні праці того часу — «Miscellanies» Франса ван Схотена й «Геометрію» Декарта. Узимку 1664—1665 років він вивчав ці книги. У цей період у працях Валліса Ньютон відкрив для себе метод нескінченних рядів. Улітку, рятуючись від епідемії чуми в рідному маєтку Вулсторп, він вирахував із їхньою допомогою площу гіперболи. Через кілька місяців Ньютон міг обчислювати похідні, й до літа 1665 року його з'ясував, що інтегрування є зворотною операцією щодо диференціювання; приблизно в цей час Ньютон вводить поняття флюксії, що позначає швидкість зміни величини функції. Автобіографічні нотатки з цього приводу були викладені в листуванні з французьким біженцем-гугенотом у Лондоні П'єром Демезо, в 1718 році почали роботу над збіркою листів вчених «Collection of Various Pieces on Philosophy, Natural Religion, History, Mathematics etc by Messrs Leibniz, Clarke, Newton and other famous Authors». Безліч інших документів підтверджують цю хронологію.

Наприкінці жовтня Ньютон почав і через кілька тижнів завершив невелике есе «How to draw tangents to mechanical lines», у якому розвинув ідею про подання функції в декартових координатах. Незабаром після цього в документі, датованому 13 листопада 1665 року, він формулює правило обчислення похідної функції багатьох змінних — досягнення, повторене Лейбніцом через 19 років. Наступний відомий рукопис, що належить до даної проблематики датується травнем 1666 року — в ньому Ньютон пов'язує поняття флюксії зі швидкістю руху. У жовтні того ж року все більш ранні роботи були об'єднані в один трактат. Написану в 1669 році статтю De analysi per aequationes numero terminorum infinitas («Про аналіз рівняннями нескінченних рядів»), оприлюднену в 1711 році, Ньютон не хотів публікувати. Він переслав цю статтю своєму вчителю й другу Ісааку Барроу, а той показав її в липні 1669 року математику Джону Коллінзу (1625—1683), який був, за висловом Річарда Вестфолла, як «математичний імпресаріо», що підтримує математичну спільноту Англії та Європи. Останній зробив із неї копію й відіслав оригінал Ньютону. Такий підхід відповідав звичаям того часу — вчені з різних причин не поспішали з оприлюдненням своїх праць. У таких випадках ці праці повідомлялися тільки найближчим друзям або віддавалися на зберігання у вчені товариства; іноді навіть сутність праці, головна формула, ховалася у вигляді анаграми. Однак дана стаття, важлива для розвитку методів диференціювання, не містила вказівок на метод флюксій і була фактично марна в подальшій полеміці про пріоритет. Спеціально присвячений цьому методу трактат «Treatise on the Methods of Series and Fluxion» (1671) був виданий після смерті Ньютона в 1736 році. Він не був завершений, але його існування зафіксовано в листуванні Ньютона. 10 грудня 1672 Ньютон написав Коллінзу лист, який доповнював його твір «De analysi», в ньому ж Ньютон визнавав, що виведені ним формули аналогічні отриманим раніше Рене де Слюзом (1622—1685) та Йоганном Гудде (1628—1704), а в розвитку свого методу він слідував вказівкам Ферма, Грегорі й Барроу:

Натяк на метод [флюксій] я отримав зі способу Ферма про проведення дотичних; застосовуючи його до абстрактних рівнянь прямо й зворотно, я зробив його загальним. М-р Грегорі й д-р Барроу застосовували й поліпшили цей метод проведення дотичних. Одна моя стаття стала причиною для д-ра Барроу показати мені його метод дотичних до включення його в 10-у лекцію з геометрії. Бо я — той друг, про якого він там згадує.

Отже, хоча за допомогою збережених документів Ньютон міг довести свій пріоритет, його праці не були відомі до початку XVIII століття широким колам науковців. Причина того, чому він не зберігав свої дослідження в архівах Королівського товариства або Кембриджського університету, була тією ж, через яку він опублікував із затримкою свою теорію кольору. У 1676 році Ньютон писав Лейбніцу через Генрі Ольденбурга:

… коли я надіслав вам лист щодо відбивального телескопа, в якому я коротко пояснив свої уявлення про природу світла, щось непередбачене змусило мене судити про необхідність поспіхом писати вам про друк цього листа. І тоді часті перебої відразу створювали листи різних людей, наповнені запереченнями та іншими питаннями, що цілком змінило мою думку й змусило мене назвати себе необдуманим, бо, щоб зачепити тінь, я пожертвував своїм миром, справді істотною річчю. Оригінальний текст (англ.) …when I had sent to you a letter on the occasion of the reflecting telescope, in which I briefly explained my ideas about the nature of light, something unforeseen made me judge it necessary to write in haste to you about the printing of that letter. And then frequent interruptions at once were created by the letters of various people filled with objections and other matters, which quite changed my mind, and caused me to call myself imprudent because, in order to catch at a shadow, I had sacrificed my peace, a truly substantial thing.

На думку англійського історика науки Альфреда Голла, у цих поясненнях Ньютон був не цілком щирий і, напевно, був просто не готовий пред'явити свої ідеї широкому науковому товаристві та розвивати їх надалі в умовах конкуренції. Існує також думка, що Ньютон не міг у цей час дозволити логічні суперечності, пов'язані з поняттям нескінченно малої величини. Радянський біограф Ньютона С. І. Вавилов вважає, що для англійського вченого математика грала допоміжну роль і виклад «Начал» у новому стилі нічого б не додало до наукової цінності його головної праці, але зробило б її незрозумілою для більшості вчених, які його б розкритикували.

До 1684 року, коли була опублікована перша робота Лейбніца з диференціального числення, Ньютон, як і раніше, не мав ніякої підготовленої до друку серйозної математичної праці, і такі його дії в цьому напрямі були пов'язані з Девідом Грегорі (1659—1708), який на основі неопублікованих праць свого дядька Джеймса Грегорі (1638—1675) далеко просунувся в техніці підсумовування рядів. Свою статтю «A Geometrical Essay on the Measuring of Figure» Грегорі відправив Ньютону в червні 1684 року, оскільки чув, що той зробив якісь відкриття в цій галузі математики. Фактично Грегорі частково відтворив висновки з ньютонівської роботи «De analysi» 1669 року. Не бажаючи займатися цим питанням, Ньютон обмежився твердженням про те, що все, повідомлене Грегорі, було йому відомо щонайменше 10 років тому, про що збереглося листування з Лейбніцом. На деякий час Ньютон зайнявся математикою, але написана в цей період стаття «Specimens of a Universal System of Mathematics» так ніколи й не була опублікована. Наступні два з гаком роки Ньютон присвятив роботі над своєю головною працею, «Математичними началами натуральної філософії». Через 2 роки Грегорі вивів основну теорему про обчислення площ фігур, обмежених кривими, отримавши від шотландського математика Джона Крега (учня й друга Ньютона) ту ж інформацію, яка в другому з листів 1676 року була повідомлена Лейбніцу. Попри попередження Крега про те, що цей результат ідентичний раніше отриманому Ньютоном, Грегорі опублікував свою теорему без згадки імені Ньютона. Ньютон не відразу отримав інформацію про цю статтю, але в 1691 році Грегорі написав Ньютону лист із проханням про допомогу в публікації «своєї» теореми. Почавши писати Грегорі відповідь, Ньютон незабаром приступив до роботи над окремим трактатом про квадратуру. До 1692 року робота під назвою «De quadratura curvarum» була практично готова, і її бачив Ніколас Фатіо де Дюйє, однак, як і в інших випадках, до публікації справа не дійшла. Частково «De quadratura curvarum» була опублікована в складі «Оптики» в 1704 році, коли ідея інтегрування вже втратила свою новизну.

Лейбніц

До початку 1670-х років Лейбніц був погано знайомий із сучасними йому досягненнями в математиці, і, хоча він із захопленням ставився до цієї науки, його основні захоплення були пов'язані з філософією, логікою і юриспруденцією. На початку 1673 Лейбніц уперше відвідав Лондон у складі Майнцського посольства. Англія в цей час особливо приваблювала його славою своїх чудових математиків і хіміків, місцем збору яких було незадовго перед тим засноване Лондонське королівське товариство. Лейбніц ще в Майнці почав листуватися зі своїм земляком Генрі Ольденбургом, який займав пост секретаря товариства. Тепер Лейбніц познайомився з ним особисто й через нього з деякими іншими членами товариства, в тому числі з хіміком Робертом Бойлом. Однак Лейбніц не відвідав ні Оксфорд, де проживав Джон Валліс, ні Кембридж, де жили Ісаак Ньютон і Ісаак Барроу. Так само не відбулася зустріч із Джоном Коллінзом, який у той час хворів. З математиків, напевно, Лейбніц зустрівся тільки з Джоном Пеллом. 29 січня він був присутній на засіданні Товариства, на якому було зачитано лист де Слюза про дотичні. Водночас Лейбніц, який продемонстрував свій механічний калькулятор, був обраний членом Королівського товариства. Серед математичних книг, які Лейбніц придбав у Лондоні, були лекції Барроу, тому є різні думки щодо впливу цієї літератури, який вона на нього справила. Відповідно до твердження самого Лейбніца, він не читав цю складну для розуміння працю. На думку А. Голл, він переглянув книгу мигцем, проте німецький історик математики Карл Гергардт аналізуючи геометричні побудови Лейбніца, сказав, що основну ідею той запозичив у Барроу.

Ймовірно, ще до поїздки в Лондон Лейбніц особисто познайомився з деякими математиками, з якими раніше тільки листувався. Серед них були французи Антуан Арно та П’єр де Каркаві й голландець Християн Гюйгенс. Останній презентував йому свою щойно видану працю про маятники Horologium Oscillatorium. Усвідомлення того, що його математичної освіти недостатньо для того, щоб зрозуміти працю Гюйгенса, але підштовхнуло Лейбніца до поглиблених занять математикою. Досить швидко він отримав значні результати щодо побудови нескінченних рядів для обчислення площі круга, на основі яких була створена теорія диференціального й інтегрального числення. Про хід цієї роботи відомо з опублікованого в 1849 році листування Лейбніца з Ольденбургом, який виступав і як безпосередній кореспондент Лейбніца, і як посередник у дипломатичному листуванні з Коллінзом. Відразу після повернення в Париж Лейбніц зустрівся з французьким математиком Жаком Озанамом (1640—1718), з яким обговорював розв'язування рівнянь. У зв'язку з цим у нього виникли нові питання, які Лейбніц поставив Ольденбургу. 16 березня 1673 року він отримав відповідь, а в отриманому 16 квітня 1673 року листі Коллінз через Ольденбурга докладно повідомляв про досягнення англійських математиків. У цьому листі ім'я Ньютона з'являлося тричі, в тому числі як винахідника загального методу обчислення площ будь-яких фігур і визначення їхніх центрів тяжіння за допомогою нескінченних рядів. Можливо, з цього листа Лейбніц уперше дізнався ім'я Ньютона, хоча ймовірно, що вони спілкувалися раніше щодо винайденого Ньютоном телескопа та інших пов'язаних з оптикою питань. Надалі математичні навички Лейбніца швидко прогресували. Продовжуючи свої математичні заняття під керівництвом Гюйгенса, він отримав нові цікаві результати в підсумовуванні нескінченних рядів, зокрема наприкінці 1673 року вираз $1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+...={\frac {\pi }{4}}$. Попри те, що ніби-то Джеймс Грегорі довів раніше неможливість розв'язати задачу квадратури круга алгебраїчно, Лейбніц і Гюйгенс вважали дане розкладання зазначенням на існування такого рішення; про це також було в листах до Ольденбурга. У тривалому листуванні Лейбніц прагнув дізнатися більше, ніж повідомляв сам. Часто Лейбніц підкреслював слова «повідомляю вам», якщо бажав, щоб Ольденбург зберігав у таємниці те чи інше, звістку про здобуті ним результати. З листування можна дізнатися, що дослідження Лейбніца відбувалися абсолютно незалежно від результатів, отриманих Ньютоном, і що Лейбніц йшов до спільної мети зовсім іншим шляхом. З нього ж можна зрозуміти, що Лейбніц не був знайомий із Коллінзом під час своєї першої поїздки в Лондон і не міг отримати від нього рукописного твору Ньютона, більш того — що Лейбніц взагалі нічого не знав про зміст цього твору.

Лист із викладенням результату про підсумовування «кругового ряду» прийшло Ольденбургу в жовтні 1674 року, і, починаючи з нього, листування Лейбніца з англійськими математиками прийняло серйозніший характер. 8 грудня Ольденбург написав обережну відповідь, у якій натякав Лейбніца не плекати в цій області великих надій на свій пріоритет. У цей момент вони обоє перебували в складній ситуації — Ольденбург не знав у точності того, чого досягли в цьому питанні Грегорі й Ньютон, а Лейбніц міг опинитися у двозначному становищі, якби опублікував свій результат. При цьому нещодавно стався конфлікт про пріоритет між Валлісом і Гюйгенсом, у результаті якого останній був виключений із Королівського товариства. Згодом пріоритет відкриття «кругового ряду» був одним із пунктів звинувачення Ньютона проти Лейбніца, оскільки Ньютон стверджував, що зробив своє відкриття ще в 1669 році, а Коллінзу повідомив про нього трохи пізніше. Через Коллінза про це дізналися Слюз у Франції й Грегорі. Отже, хоча Лейбніц відкрив свій ряд незалежно, він мав можливість дізнатися про нього з декількох джерел, тому до 1675 року листування Лейбніца з Ольденбургом перестало приносити нову інформацію для них. Коли Лейбніц в одному з листів поставив питання про те, чи може хто-небудь з англійських математиків обчислити довжину дуги еліпса або гіперболи, Ольденбург чекав три місяці, перш ніж відповісти, що можуть, але тільки приблизно, хоча з будь-якою заданою точністю — а детальнішу інформацію може розповісти прибулий до Парижа математик-аматор Чирнгауз (1651—1708). Ймовірно, англійці припускали, що від Чирнгауза Лейбніц міг отримати деталі про стан справ в англійській математиці. Однак, судячи із записів Лейбніца, його спілкування з Чирнгаузом у Парижі було дуже коротким і до листопада 1675 роки не стосувалося математики. Наприкінці 1675 Лейбніц готувався до від'їзду в Ганновер і збирався опублікувати свої математичні праці. На тлі війни Франції з Нідерландами ускладнилися його відносини з Гюйгенсом. До цього ж часу належить визначний лист, у якому Лейбніц викладає Ольденбургу свою концепцію метанауки, покликаної дати відповідь на всі питання, в якій його диференційний метод посяде чільне місце.

У травні 1675 в Англію приїхав молодий німецький учений Еренфрід фон Чирнгауз, який познайомився там із багатьма відомими науковцями й до вересня вирушив у Париж, де здружився з Лейбніцом і займався разом із ним математикою. У 1725 році, тобто після смерті Чирнгауза, було вперше висловлено звинувачення в тому, що Лейбніц від нього отримав знаменитий лист Ньютона до Коллінза, написаний у 1672 році. На деякий час листування Лейбніца з англійськими математиками перервалося. У жовтні 1675 року помер Джеймс Грегорі, Коллінз знаходився в складному становищі й побоювався втратити роботу (що й сталося влітку наступного року), Ольденбург був залучений у суперечку між Ньютоном і континентальними критиками його теорії світла, а сам Ньютон більшу частину часу присвячував своїм алхімічним заняттям. У результаті комерційного провалу книги Барроу книгопродавці відмовилися працювати з математиками без виплати грошей ними, що зробило проблематичною появу нових книг у цій галузі. Листування Лейбніца з Ольденбургом і Коллінзом відновилася в травні 1676 року за ініціативою англійців. У новому листі містилися розкладання в ряд для синуса й косинуса, які надсилались йому роком раніше, про що Лейбніц, мабуть, забув. Він попросив доказ їхнього виведення, яке йому було надіслано. Восени 1676 Лейбніц прийняв пропозицію герцога Ганноверського Ернста Августа зайняти місце його бібліотекаря й покинув Париж, у якому проживав з 1672 року. Він відправився в Ганновер через Англію й Голландію, провівши тиждень у Лондоні в жовтні 1676 року. У цей час англійські кореспонденти Лейбніца ставилися до нього добре. Коллінз писав про «неперевершеного пана Лейбніца»; Ольденбург також позитивно відгукувався про нього.

Ньютон і Лейбніц

Перша сторінка статті Г. В. Лейбніца «Nova Methodus pro Maximis et Minimis», Acta Eruditorum, 1684 рік

Після того, як Коллінз і Ольденбург у травні 1676 року дізналися про поновлення Лейбніцом занять з математики, вони почали збирати наявні в їхньому розпорядженні документи й листи для пересилання. У пакет були включені наявні в розпорядженні Коллінза звіти про досягнення Грегорі та інших англійських математиків за останні кілька десятиліть — так звана «Historiola» обсягом у 50 сторінок. Тим часом Ольденбург звернув увагу Ньютона на успіхи Лейбніца, в результаті чого Ньютон написав через нього Лейбніцу лист, у якому повідомив про свой біном. Ольденбург відправив лист 26 липня 1676 року й при цьому вперше згадав про лист Ньютона до Коллінза від 10 грудня 1672 року. Перший лист Ньютона Лейбніцу — 11 сторінок на латині — було видано в третьому томі «Mathematical Works» Джона Валліса з неправильним зазначенням дати відправлення — 6 липня. Згодом Ньютон неодноразово повторював цю помилку, дорікаючи Лейбніца в тому, що він вивчав лист три тижні, перш ніж дати відповідь. Так само Ньютон помилково вважав, що з цим листом Лейбніцу була переслана «Historiola» (тоді вона була відправлена ​​в скороченому й неточному перекладі на латинь), тому Лейбніц працював із цим об'ємним документом усе літо перед поїздкою до Лондона. Насправді Лейбніц отримав лист 16 серпня й на наступний день відправив Ньютону ґрунтовну відповідь, у якій розповів йому про винайдене ним диференціальне числення, не повідомивши, однак, подробиць. Щодо того, наскільки відвертим був у цьому листі Ньютон, є протилежні точки зору: біограф Лейбніца Йозеф Гофман вважає, що Ньютон зробив усе, щоб не повідомити Лейбніцу головне про свій метод флюксій, тоді як Альфред Голл пов'язує відсутність деяких подробиць із тим, що до цього часу в Ньютона просто не було належним чином підготовлених робіт на цю тему.

У жовтні 1676 Лейбніц відправився вдруге в Лондон, де провів приблизно тиждень. Тоді йому вдалося побачити твір «De Analisi», який Ньютон написав у 1669 році, й зробити виписки з нього, які були знайдені в недатованих паперах Лейбніца. Але в цьому витязі Лейбніц всюди вживає власні знаки інтегрального та диференціального числення, що може вказувати на те, що він познайомився з твором Ньютона вже після того, як зробив свій винахід. Можливо, він отримав його від Ольденбурга під час своєї другої поїздки в Лондон. У цю коротку поїздку Лейбніц нарешті зустрівся з Коллінзом і отримав повну версію «Historiola». Другий лист Ньютона до Лейбніца, невеликий трактат обсягом 19 сторінок, був завершений 24 жовтня, однак Лейбніц не встиг його отримати. Він пролежав в Ольденбурга до весни наступного року, поки той не знайшов можливості переслати його в Ганновер. У цьому листі Ньютон повідомляє Лейбніца про свій винахід, не вдаючись у подробиці. Головна формула повідомлена у вигляді анаграми. У відповідь на цей лист Лейбніц через Ольденбурга викладає йому підстави свого диференціального обчислення, не повідомляючи про своє знайомство з твором 1669 року й алгоритмом обчислення інтегралів. У листопаді 1676 року відбувалося листування між Ньютоном і Коллінзом. Коллінз безрезультатно намагався переконати Ньютона опублікувати свої праці з математичного аналізу, у відповідь на що Ньютон запевняв у перевазі свого методу над тим, який винайшов Лейбніц. Ще кілька місяців після цього Коллінз повідомив Ньютону про візит Лейбніца й про те, що обговорювалися папери Грегорі. Про те, що Лейбніц бачив папери Ньютона, Коллінз промовчав і помер у листопаді 1683 року, тому й не розповів. На лист Лейбніца Ньютон не відповів, а в серпні 1678 року помер Ольденбург, і на наступне десятиліття вчені припинили спілкування.

Як і Ньютон, Лейбніц не поспішав із поширенням своїх відкриттів. До публікації статті Лейбніца «Новий метод максимумів і мінімумів, а також дотичних, і простий спосіб їхнього обчислення» в журналі «Acta eruditorum» у жовтні 1684 року майже ніхто про його досягнення не знав. За цією короткою й незрозумілою статтею, в якій викладалися основні правила диференціювання, слідувала низка інших на ту ж тему. Оскільки цей журнал не входив до основних математичних видань свого часу, й оскільки ніхто не міг припустити інтересу Ньютона до даної публікації Лейбніца, її шлях із Лейпцига в Кембридж зайняв близько року. Ньютон відразу зрозумів важливість статті й зіставив її з листуванням 1676 року, для нього було очевидно, що «метод флюксій» і «диференціальне обчислення» показують одну й ту саму математичну ідею. У «Математичних засадах натуральної філософії», що вийшли в 1687 році Ньютон застосував метод флюксій тільки один раз, під час доказу Леми II в другій книзі («Момент добутку дорівнює сумі моментів окремих виразів, помножених на показники їхніх ступенів і коефіцієнтів»), що відповідає правилу диференціювання добутку. У подальшому викладі «моменти» практично не використовуються, можливим поясненням введення даної леми є додавання автобіографічного зауваження:

У листах, якими близько десяти років тому я обмінювався з вельми майстерним математиком Г. В. Лейбніцом, я йому повідомляв, що знаю метод для визначення максимумів і мінімумів, проведених дотичних і рішення тому подібних питань, однаково застосовні як для членів раціональних, так і ірраціональних, причому я її сховав, переставивши літери наступного речення: «data aequatione quotcumque fluentes quantitates involvente fluxiones invenire et vice verca» (коли задано рівняння, що містить будь-яке число змінних кількостей, знайти флюксії й навпаки). Славнозвісний чоловік відповів мені, що він також дослідив такий метод, і повідомив мені про свої дослідження, які ледь відрізняються від моїх, і то тільки термінами й накресленням формул.

Отже, в 1687 році Ньютон не претендував на те, щоб пояснити досягнення Лейбніца отриманої від нього інформації. Під «vice verca» тут розумілося зворотне до диференціювання інтегрування, тобто метод обчислення площ фігур, обмежених кривими, — його Ньютон, згідно з вищенаведеною цитатою, також не повідомляв Лейбніцу. Більш ніяких кроків для захисту свого пріоритету Ньютон не вжив. Як зауважив англійський історик науки Том Вайтсайд, у цей час Ньютону не вистачило рішучості, проявивши яку, він би уникнув величезних занепокоєнь через чверть століття.

Поширення диференціального числення

Опублікована 1684 року стаття «Новий метод максимумів і мінімумів» не отримала визнання, й навіть апологети нового методу, брати Бернуллі, назвали її «загадковою». У наступній своїй статті 1686 року присвяченій інтегруванню, Лейбніц (на відміну від попередньої) перерахував своїх попередників, до яких відніс і Ньютона, проте висловився досить невизначено: «Ньютон підійшов до відкриття квадратур за допомогою нескінченних рядів не тільки абсолютно незалежно, але він настільки доповнив метод взагалі, що видання його робіт, досі не отримало здійснення, стало б безсумнівно приводом нових великих успіхів у науці». Там же Лейбніц говорить, що деякі з його ідей уже були використані, хоча і з помилками. За припущенням Альфреда Голла, мова йде про шотландського математика Джона Крега, який отримав номер журналу від Девіда Грегорі й, на відміну від останнього, зрозумів переваги алгоритму Лейбніца. У цей період Крег займався проблемою визначення площ фігур, і він звернув увагу на корисність інтегралів для вирішення цього завдання. Судячи з усього, Крег не знав про внесок Ньютона в розвиток диференціального числення. Попри те, що Крег написав кілька книг із використанням нового методу, значного внеску в теорію він не вніс. У 1687 році, через два роки після Крега, про статтю Лейбніца стало відомо швейцарському математику Якобу Бернуллі (1655—1705), який разом зі своїм братом Йоганном (1667—1748) працював над завданнями математичного аналізу. До цього часу брати вже познайомилися з обчисленням нескінченно малих Валліса й Барроу. У своїй написаній через багато років «Автобіографії» Йоганн Бернуллі писав, що на те, щоб розібратися з «Новим методом» Лейбніца, йому з братом було потрібно декілька днів. У 1690 році Якоб Бернуллі опублікував статтю, в якій застосував метод Лейбніца до ізохронної кривої, а в наступному році Йоганн розв'язував задачу про ланцюгову лінію. На початку 1690–х років брати Бернуллі почали листуватися з Лейбніцом. На відміну від Ньютона й Лейбніца, вони мали велике число учнів у різних країнах. Восени 1691 Йоганн Бернуллі приїхав до Парижа. Там його добре прийнятли в гуртку інтелектуалів картезіанця Ніколя Мальбранша, який зацікавився методом Лейбніца з визначення кривини кривих. У Парижі Бернуллі-молодший уклав контракт на навчання математиці маркіза Лопіталя (1661—1704). Маркіз, своєю чергою, наприкінці 1692 року написав листа Лейбніцу, з якого випливало, що вже в кінці 1688 року він познайомився зі статтею німецького математика. У період свого перебування в Парижі Бернуллі навчив методу Лейбніца кількох членів гуртка Мальбранша: священника Луї Бізанса й математиків Шарля Рене Рейно, П'єра де Монмора й П'єра Варіньона. У 1696 Лопіталь, якого Бернуллі продовжував навчати через листування після від'їзду з Франції, видав перший підручник математичного аналізу, що охоплює питання диференціювання. Книга була дуже успішною й зміцнила славу маркіза як математика. Нині встановлено, що її текст в основному був написаний Йоганном Бернуллі. Друга частина підручника, в якій передбачалося розповісти про інтегрування, вийшла тільки в 1742 році. Мальбраншіст П'єр Варіньон, підтримував стосунки як із Лейбніцем, так і з Ньютоном, став найбільш послідовним пропагандистом нової теорії.

Рух тіла різними траєкторіями. Червона лінія — брахістохрона

Хоча поширення ідей аналізу відбувалося досить швидко, були й критики. Їхні заперечення ґрунтувалися на хиткості логічних підстав обчислення нескінченно малих. Лейбніц, хоч і докладав зусиль для побудови надійного математичного обґрунтування своєї теорії, загалом дивився на проблему простіше, ніж Ньютон, — головне, що теорія працювала. У цьому відношенні була показова реакція Християна Гюйгенса, якому в ряді листів Лейбніц виклав принципи свого аналізу. Старий голландський математик відреагував на послання Лейбніца негативно. Він сам розробляв подібну теорію, однак не планував її оприлюднювати, бо не мав можливості придумати її ґрунтовне доведення. Більш перспективними Гюйгенс вважав підходи, про які йому з Лондона повідомляв швейцарець Ніколас Фатіо де Дюйє (1664—1753), який займався завданнями інтегрування. Хоча Гюйгенс так і не погодився з тим, що робота Лейбніца почала нову еру в математиці, в одному зі своїх останніх листів він визнав важливість досягнення німецького математика. Як зазначає А. Голл, ні в кого з трьох найбільших математиків свого часу — Гюйгенса, Ньютона й Лейбніца — не було непорозумінь щодо можливостей і значущості теорії математичного аналізу, однак вони по-різному оцінювали природу цього відкриття. Чи було це, як вважали Гюйгенс і Ньютон, еволюційний розвиток дотеперішніх методів, або ж щось абсолютно нове? Згодом Лейбніц посилався на визнання Гюйгенса як на одне з найбільш вагомих доказів його пріоритету. Ньютон відкидав цей доказ, оскільки, на його думку, Гюйгенс не опанував теорію аналізу.

Після смерті Гюйгенса в 1695 році Лейбніц став загальновизнаним лідером континентальної математичної школи. Аналогічне становище в Англії займав Ньютон, однак він не виставляв назагал свої роботи й займався державною службою та алхімічними дослідженнями. Досягнення континентальних математиків в Англії були практично не відомі, проте в 1696 році за ініціативою Йоганн Бернуллі відбулося змагання найбільших європейських математиків. Їм було запропоновано завдання визначення кривої, за якою тіло під дією сили тяжіння скотиться з однієї точки в іншу — завдання про брахістохрону. В Англії завдання було відправлене Ньютону й Валлісу. Лейбніц розв'язав задачу в день отримання, проте не зміг визначити, що рішення описує циклоїду. За твердженням Ньютона, він теж швидко розв'язав задачу. Пізніше, роблячи підсумки змагання, Лейбніц серед тих, хто сказав правильну відповідь, назвав також Якоба Бернуллі й Лопіталя (який отримував допомогу від Йоганна Бернуллі). Вирішення цього завдання вимагало знання математичного аналізу, і, як підозрював Ньютон, завдання було відправлене ​​йому, щоб довести меншу потужність його методу флюксій.

Перебіг спору

Перші звинувачення: 1691—1711 роки

Суперечка між Ньютоном і Лейбніцом стала прилюдною завдяки швейцарському математику Ніколасу Фатіо де Дюйє. У 18 років цей мешканець Базеля прибув до Парижа, де працював в обсерваторії Джованні Кассіні. Через 2 роки вони разом описали явище зодіакального світла. У 1686 році Фатіо де Дюйє познайомився з Якобом Бернуллі й Християном Гюйгенсом. Спільно з останнім він займався вивченням дотичних. На початку 1687 року Фатіо де Дюйє приїхав у Лондон, де познайомився з багатьма англійськими математиками. У наступному році він був прийнятий у Королівське товариство, на одному із засідань якого він познайомився з Ньютоном. Незабаром між ними виникла настільки тісна дружба, що американський історик Френк Меньюел запідозрив у ній «потужне гомосексуальне почуття». Фатіо де Дюйє мав можливість ознайомитися з трактатом «De quadratura curvarum», що готується Ньютоном до оприлюднення. Оскільки ще раніше він через Гюйгенса дізнався про роботи Лейбніца в галузі аналізу, йому стало очевидно, що підходи обох математиків до вирішення завдань диференціювання й інтегрування збігаються з точністю до позначень. 28 грудня 1691 року Фатіо де Дюйє пише лист Гюйгенсу, в якому вперше прозвучало звинувачення Лейбніца в плагіаті. У лютому наступного року він продовжує цю тему, вказуючи на факт листування між Ньютоном і Лейбніцем. Одночасно з цим Джон Валліс, бувши прихильником відстоювання наукового пріоритету Англії, переконував Ньютона оприлюднити свої математичні дослідження й листи 1676 року. Не добившись нічого, він включив згадку про метод флюксій до другого тому своїх «Математичних праць» у 1693 році. Там же Валліс виклав свою версію пріоритету: метод Лейбніца, аналогічний методу Ньютона, хоча і є його погіршеною копією; обидва вони ґрунтуються на методі Барроу, який, своєю чергою, посилається на розроблену самим Валлісом теорію нескінченних рядів. Проте А. Голл вважає, що до 1695 Ньютон не думав, що його права першовідкривача були обмежені. Більш того, в цей період Ньютон і Лейбніц відновили листування, і Лейбніц сам просив Ньютона видати покращене видання «Начал». У 1696 Лейбніц ознайомився з працею Валліса й зазначив, що метод Ньютона знаходиться схожий з його методом. Йоганн Бернуллі також вивчив книгу Валліса й вирішив, що Ньютон міг створити свій метод на основі аналізу Лейбніца. Своїми міркуваннями він поділився з Лейбніцем, який спочатку не був готовий підтримати цю тезу.

До кінця 1690-х років у континентальній Європі, як і раніше, ніхто не знав про досягнення Ньютона і, тим більше, про їхню хронологію. Схолія до Леми II в «Засадах» не залишилася непоміченою, але, наприклад, П. Варіньйон зрозумів її в тому сенсі, що Ньютон був знайомий з аналізом Лейбніца. У 1699 році Валліс видав третій том своїх творів, до якого увійшли обидва листи 1676 року, а також раніші документи, що доводять прогрес досліджень Ньютона. У цьому ж році Фатіо де Дюйє опублікував трактат «Lineae brevissimi descentus investigatio geometrica duplex» («Подвійне геометричне дослідження лінії найкоротшого спуску»), у якому повернувся до задачі про брахістохрону 1696 року. До цього часу він уже шість років не підтримував відносин із Ньютоном, і немає підстав вважати, що той був якось причетний до появи цієї праці — однак Лейбніц, який знав про їхню дружбу, був у цьому впевнений. У своєму «Дослідженні» Фатіо де Дюйє прямо звинуватив Лейбніца в плагіаті. Той, своєю чергою, отримавши примірник статті від Лопіталя, опублікував в «Acta eruditorum» анонімну рецензію, в якій спростував ці звинувачення, заявивши про знайомство тільки з методом дотичних Ньютона. Тоді ж Лейбніц анонімно розкритикував продемонстроване Девідом Грегорі розв'язання задачі про ланцюгові лінії. Хоча це рішення було дійсно помилковим, Лейбніц пішов далі й в особі Грегорі зробив висновки про помилковість теорій математиків школи Ньютона. Авторство Лейбніца в цих двох статтях було доведено в 1711 році, що серйозно позначилося на його репутації. У 1701 році був виданий перелік помилок у ньютонівських «Засадах», і, хоча список був насправді складений самим Ньютоном і переданий Гюйгенсу Фатіо де Дюйє, в Англії були впевнені в причетності Лейбніца. У таких обставинах Ньютон у 1702 році пообіцяв своїм друзям опублікувати «Оптику» й ще два математичні трактати («De quadratura curvarum» і «Enumeratio linearum tertii ordinis»), що й було виконано через 2 роки. У передмові він вказав, що ці роботи випливають із його нотаток 1670–х років, давно відомим Лейбніцу. Згідно з Ньютоном, метод флюксій, використаний у «De quadratura» для обчислення квадратур, був розроблений ним ще в 1665 році. У січні 1705 року в «Acta eruditorum» вийшла анонімна рецензія, яка була, як нині відомо, написана Лейбніцом (сам Лейбніц у цьому ніколи не зізнавався, але Ньютон був упевнений у його авторстві). У цій рецензії стверджувалося, що флюксії Ньютона відповідають поняттю, використаному французьким математиком Оноре Фабрі (1607—1688), й ранішому методу Кавальєрі, а результати Ньютона викладалися в термінах диференціалів Лейбніца. Хоча явного звинувачення в плагіаті не прозвучало, багатьма (в тому числі й Ньютоном) це було сприйнято саме так. У 1708 році учень Ньютона Джон Кейлл спростував ці інсинуації в статті «On the Laws of Centripetal Force»:

Усі ці теорії випливають із сьогоднішньої прославленої Арифметики флюксій, яку містер Ньютон, поза всяким сумнівом, винайшов першим, оскільки кожен, хто читає його листи, опубліковані Воллісом, може легко визначити; одна й та ж «Арифметика» під іншою назвою та з використанням різних позначень згодом була опублікована в Acta eruditorum паном Лейбніцом Оригінальний текст (англ.) All of these [propositions] follow from the now highly celebrated Arithmetic of Fluxions which Mr. Newton, beyond all doubt, First Invented, as anyone who reads his Letters published by Wallis can easy determine; the same Arithmetic under a different name and using different notation was later published in the Acta eruditorum, however, by Mr. Leibniz

Причини, через які Кейлл вирішив захистити Ньютона, незрозумілі. Можна припустити, що цей виступ мав стосунок до ширшого контексту розбіжностей між англійськими й континентальними вченими з питання про природу сил і будову всесвіту. Номер «Філософських праць Королівського товариства» з цією статтею був опублікований у 1709 році, й Ньютон пізніше стверджував, що не знав про цей пасаж Кейлла. Однак з огляду на те, що стаття була попередньо зачитана на засіданні Королівського товариства 3 листопада 1708 року, це малоймовірно. Необхідно зазначити, що Кейлл був одним з оксфордських друзів Ньютона. Невідомо, коли Лейбніц ознайомився зі статтею Кейлла, але офіційний лист із протестом у Королівське товариство він направив у березні 1711 року.

Підготовка до війни: 1711—1713 роки

Готфрід Вільгельм Лейбніц, портрет бл. 1710 року

Кейлл фактично висловив спільну думку, що склалася в науковій спільноті Англії. Фізик Джордж Чейн у своїй праці «Зворотний метод флюксій» 1703 року писав, що за останні 20—30 років у математиці не з'явилося нічого, що не було б повторенням або тривіальним наслідком попереднього відкриття Ньютона. Погляди Чейна, що приписують усі наукові досягнення свого часу англійцям і замовчують досягнення континентальних вчених, були зазначені Йоганном Бернуллі, назвавши Чейна і йому подібних до «мавп Ньютона». Ставлення Лейбніца до англійських учених також стало гіршим, і з цього часу в його листуванні з'являється тема приниження досягнень Ньютона. Наступні 5 років сторони утримувалися від масштабної боротьби. Лейбніц не вступав у суперечку з Чейном та Фатіо де Дюйєм, Ньютон очолив Монетний двір, Королівське товариство й став лицарем. З 1708 року обговорювався архів Джона Коллінза, що містить невідомі до цього широкій науковій громадськості ранні роботи Ньютона, у тому числі «De analysi» 1669 року. Також там були листи, з яких випливало, що Лейбніц про ці праці знав — про що ніколи не згадував. 31 січня 1711 року, за два місяці до отримання листа Лейбніца, уривки цього архіву на засіданні Королівського товариства представив доктор Річард Мід. Підбірка матеріалів і попередній їхній вступ відкинув усі сумніви щодо пріоритету Ньютона. Лейбніц у своїй анонімній рецензії на «De analysi», нічого не кажучи про дати, заявив, що суть викладеного в цьому трактаті методу зводиться до розвитку методів вичерпання Архімеда й нескінченно малих Ферма. Водночас у публічних заявах Лейбніц завжди висловлювався про Ньютона з великою шанобливістю. Отже, аж до 1711 року обидва учасники конфлікту утримувалися від прямих нападок один на одного, діючи через своїх прихильників.

Лист зі спростуванням «зухвалих звинувачень» Кейлла було отримано Королівським товариством 4 березня 1711 року. У ньому Лейбніц висловлював побоювання, що ці звинувачення будуть повторюватися безчесними людьми, завдаючи шкоди його репутації. Оскільки обидва вони (Лейбніц і Кейлл) були членами Товариства, Лейбніц зажадав, щоб було надане офіційне спростування. Під керівництвом Ньютона 22 березня відбулося засідання Товариства, на якому лист було зачитано. Згідно з протоколом, секретарю Товариства Гансу Слоуну було доручено скласти відповідь, однак цей документ не зберігся й навряд чи був узагалі написаний. Через два тижні (15 квітня) питання було знову розглянуто й знову під головуванням Ньютона; на це засідання з Оксфорда прибув Кейлл. У протоколі зборів констатувалося, що у випуску Acta eruditorum за 1705 рік Лейбніц зробив помилкове твердження про суть математичних досягнень Ньютона й справжнє їхнє авторство, на що було вказано у свій час Кейллом. Через тиждень Ньютон зробив приписку зі згадуванням своїх листів Коллінзу. Збереглися документи, що свідчать про бурхливі ​​активності в ці тижні — учасники подій обмінювалися листами, Ньютон перечитував свої старі документи й відновлював у пам'яті хронологію подій. Складена Кейллом остаточна відповідь Лейбніцу була затверджена на засіданні Товариства 24 травня. Передбачалося, що вона буде опублікована, коли Лейбніц підтвердить отримання, проте цього так і не відбулося. Лейбніц довго обмірковував свою відповідь. Його лист був відправлений 29 грудня й отриманий Королівським товариством у січні 1721 року. У ньому Лейбніц не претендував на його метод флюксій, схожий, однак, із його власним методом. Першою реакцією Ньютона, про що свідчать збережені чернетки, було написати Слоуну, що він не буде вступати в цю дискусію. Однак поступово ця тема захопила його, особливо після того, як йому доставили рецензію на «De analysi», що вийшла в лютому. Листи він так і не написав, але 6 березня 1712 року Королівське товариство призначило комісію для вивчення листів і паперів, що належать до цього питання. До її складу увійшли члени Товариства, зокрема математики Джон Арбутнот, Едмонд Галлей, Вільям Джонс, Джон Мечін, торговець і автор біографії Ісаака Барроу Абрагам Гілл, чиновник Вільям Бернет. 17 квітня до них приєдналися політик Френсіс Робартес, математики Абрагам де Муавр і Брук Тейлор, Френсіс Астон (математик) і посол Пруссії Фредерік Бонет — за висловом Ньютона, це був «численний і вдалий збір джентльменів декількох націй».

Робота комісії не мала б бути дуже складною — Ньютон підготував усі матеріали, додавши до архіву Коллінза листи Ольденбурга, 24 квітня він сам підготував звіт, який стверджував його власні права як «першого автора» аналізу. Лейбніца не звинувачували явно в плагіаті, його провиною вказувалося порушення наукової етики, що виразилося в приховуванні факту використання відомої йому інформації. На основі цього документа було підготовлено й видано на початку наступного року збірку «Commercium epistolicum D. Johannis Collis, et aliorum de analysi promota» («Листування вченого Джона Коллінза та інше, що належить відкриттю аналізу»). Видання вийшло невеликим накладом і не призначалося для продажу. 25 копій було послано шотландському книгопродавцю в Гаагу й найбільшим континентальним математикам, «здатним оцінювати подібні речі». «Commercium epistolicum» містив раніше відомі тексти, забезпечені поясненнями, що наголошують на крадіжці чужих ідей, якими постійно, на думку автора, займався Лейбніц. Нова низка доказів, обрана Ньютоном, включала також твердження, що свій метод флюксій він використовував у «Засадах», що нібито підтверджували відправлені в 1683 році в Королівське товариство фрагменти його незакінченої праці. Оскільки дата цього передбачуваного повідомлення передувала публікації Лейбніцем його першої статті, це могло б бути істотною обставиною, проте такої події насправді не було. У висновку комісії Королівського товариства йшлося: «з цих підстав ми вважаємо Ньютона першим винахідником і думаємо, що Кейлл, стверджуючи це, не зробив нічого поганого стосовно Лейбніца».

Прилюдна суперечка: 1713—1715 роки

Загальне враження, створене публікацією «Commercium epistolicum», було настільки сильним, що навіть віддані прихильники Лейбніца — Варіньйон і Бернуллі — були неприємно вражені тим, що їхній учитель майже 30 років здобув не цілком заслужену славу. Бернуллі й Християн Вольф прохали Лейбніца написати власну версію історії математичного аналізу. Робота над цією працею була розпочата в 1714 році, але не була закінчена. Не маючи можливості спростувати аргументи Ньютона в питанні про пріоритет у відкритті математичного аналізу або хоча б довести, що Лейбніц домігся важливих досягнень до отримання другого листа Ньютона, його засуджували через два інші напрями. По-перше, піддавалася сумніву компетентність Ньютона як математика — прихильники Лейбніца розшукували помилки в його працях, насамперед в «Математичних началах натуральної філософії». Найбільш послідовним критиком Ньютона в 1710–х роках був Йоганн Бернуллі, великий резонанс мала виявлена ​​його племінником Миколою Бернуллі «помилка» Ньютона в диференціюванні. По-друге, оскаржувалися положення ньютонівської теорії тяжіння. Для континентальних вчених, які схилялися до поглядів Декарта, що введенні Ньютоном взаємодії через сили здавалися вкрай сумнівними. Усі контраргументи були зібрані й видані у вигляді анонімної листівки, що увійшла в історію як «Charta Volans» (1713), у якій Лейбніц називався єдиним винахідником аналізу, похідним від якого був метод Ньютона. Печаткою й поширенням цього памфлету займався Християн Вольф. Восени 1713 років через літератора Джона Чемберлейна документ потрапив у руки Ньютона, який повернувся до своєї колишньої пасивної тактики. Ймовірно, він не вважав за необхідне реагувати на анонімні звинувачення й очікував більш офіційної відповіді на «Commercium epistolicum». Однак він вважав, що якусь відповідь дати необхідно, якщо вже Лейбніц зробив цей конфлікт публічним. Цим мав зайнятися Кейлл.

У номері за травень — червень 1713 року журналу «Journal littéraire de La Haye» Кейлл опублікував велику статтю про історію аналізу, в якій для французької аудиторії викладалася версія з «Commercium epistolicum», доповнена на основі звинувачень Фатіо де Дюйє. З нових документів було опубліковано лист Ньютона Коллінзу від 10 грудня 1672 року. Наприкінці того ж року Лейбніц дав відповідь («Remarks on the Dispute», «Зауваження про диспут»), у якій заявив, що нічого не знав про претензії Ньютона на пріоритет до публікації «Commercium epistolicum» і чекає, що Ньютон заспокоїть своїх занадто завзятих прихильників. Також він зазначив, що ніколи не давав себе судити Королівському товариству, якому його точка зору не була донесена. Коли Ньютон приховав свій метод, Лейбніц діяв навпаки. При цьому власний метод Ньютона був не такий уже й досконалий, як це було показано таким собі «відомим математиком» (тобто Йоганном Бернуллі). Після цього була опублікована французька версія «Charta Volans».Отже, в подальшому Ньютону було необхідно доводити не тільки свою історичну правоту, але також правильність свого методу; з тезою про більше моральне право Лейбніца на відкриття він сперечатися не міг. Найважливіше для нього було спростувати звинувачення в скоєнні помилок. Зберіглася чернетка листа, в якій Ньютон доводить, що Лейбніц не розуміє різницю між своїми похідними і його флюксіями — згідно із сучасними уявленнями ця різниця практично несуттєва. Улітку 1714 року було опубліковано «Відповідь» Кейлла авторам «Зауважень» — на його думку, під «відомим математиком» мався на увазі Християн Вольф. Тим часом Й. Бернуллі, з одного боку, добре вивчив і добре оцінив роботи Ньютона, які стали відомими, з іншого боку, з огляду на свою критику «помилок» «Математичних начал», побоювався можливості виключення з Королівського товариства. Відповідно до цього він, як і раніше підтримуючи позицію Лейбніца, пропонував йому уважніше вивчити «Commercium epistolicum».

До середини 1714 року суперечка згасла. Континентальна Європа в цілому прийняла сторону Лейбніца — за винятком нідерландського журналу «Journal littéraire de La Haye», одним із редакторів якого був ньютоніанець Вільгельм Якоб Гравезанд. У Франції окрему думку висловив старий картезіанець де Фонтенель, який зазначив, що Лейбніц продовжив думку Барроу. Ця позиція була ближче до англійської, і з плином часу через політичні й особисті обставини різних вчених, у Франції вона стала посилюватися. Установлення в Англії в 1714 році Ганноверської династії нічого не дало Лейбніцу, який не зміг заручитися підтримкою впливових політиків. В останній період свого життя Лейбніц покинув спроби довести свій пріоритет і зосередився на філософських проблемах. Найважливішим епізодом тут було листування із Семюелем Кларком щодо філософських основ фізики, що стала заочною суперечкою з Ньютоном. З боку Ньютона в 1715 році вийшло дві публікації: його власна опублікована анонімно стаття «Account of the Book entitled Commercium Epistolicum… published by order of the Royal Society» («Звіт про книгу під назвою „Commercium epistolicum“, виданої за розпорядженням Королівського товариства») і книга математика Джозефа Рафсона «Історія флюксій». Рафсон, що не належав до кола Ньютона, спробував історично дослідити питання про пріоритет на основі доступних йому джерел і вирішив, що Лейбніц зміг отримати цінну інформацію з листів Ньютона. Його вердикт був такий: «Чи запозичив Лейбніц метод, або винайшов сам, не має жодного значення, бо другий винахідник не має прав». Ньютон, хоча й заперечував спочатку свою зацікавленість у цьому виданні, після смерті Лейбніца перевидав книгу без змін. «Звіт», належність якого Ньютону стала відома тільки в 1761 році, вкотре детально підсумовував розбіжності з Лейбніцом за п'ятьма напрямками, починаючи з історії математичного аналізу і його співвідношення з методом флюксій і до філософських питань. В Англії ця робота була прийнята як авторитетне джерело, в Європі залишилася практично непоміченою; в листопаді 1715 року вийшов її французький переклад.

Згасання суперечки. Після 1715 року

Лейбніц так ніколи й не погодився визнати пріоритет Ньютона у винаході математичного аналізу. Він також намагався написати власну версію історії диференціального обчислення, але, як і у випадку з історією правителів Брауншвейгу, не завершив справу. Наприкінці 1715 Лейбніц прийняв пропонову Йоганна Бернуллі влаштувати ще одне змагання математиків, у якому різні підходи повинні були довести свої знання. На цей раз завдання було взято з галузі, пізніше названої варіаційним обчисленням, — потрібно побудувати дотичну до сімейства кривих. Лист із формулюванням було написано 25 листопада й передано в Лондоні Ньютону через абата Антоніо Конті. Завдання було сформульоване в не дуже чітких термінах, і тільки пізніше з'ясувалося, що було потрібно знайти спільне, а не приватне, як це зрозумів Ньютон, рішення. Після того, як англійці опублікували своє рішення, Лейбніц опублікував своє, загальніше, й переміг у цьому змаганні. Зі свого боку, Ньютон наполегливо прагнув перемогти свого опонента. Не добившись цього зі «Звітом», він продовжив свої дослідження, витрачаючи на це сотні годин. Приводом для його наступного дослідження, названого «Observations upon the preceding Epistle» («Спостереження щодо попереднього листа»), став лист Лейбніца Конті березня 1716 року, в якому критикувалися філософські погляди Ньютона; нових доказів у цьому документі наведено не було. Зі смертю Лейбніца в листопаді 1716 року суперечка поступово затихла. На думку А. Голла, після 1722 року це питання перестало цікавити самого Ньютона.

В Англії в перемозі Ньютона в цій суперечці ніколи не сумнівалися. Хоча погані відгуки про роль Лейбніца в англомовній літературі зустрічалися аж до XX століття, вже за часів королеви Вікторії почали звучати й інші думки. У 1920 році американський математик Артур Гезевей, бувши впевненим, що Лейбніц не міг самостійно зробити свої відкриття, називав його засновником німецького наукового шпигунства, що, на його думку, підтверджує випадок із Джоном Пеллом (див. вище^[⇨]). До середини XX століття суперечки вщухли, англійські історики оцінили заслуги Лейбніца, а німецькі визнали пріоритет Ньютона.

Питання про порівняльні переваги запису диференціювання Лейбніца (${\frac {dx}{dt}}$) і Ньютона (${\dot {x}}$) обговорювалося впродовж XVIII століття. Англійська система була відома в континентальній Європі, але не дуже популярна. У 1755 році Л. Ейлер зазначав незручність позначення похідних високих ступенів, що призводить до нагромадження крапок над знаком функції. Порівняльне дослідження англійця Роберта Вудгауза (1802) й француза Сильвестра Лакруа (1810) також надали перевагу запису Лейбніца. Його успіх остаточно закріпили зусилля Джона Гершеля, Джорджа Пікока й Чарльза Беббіджа в Кембриджі. З наукової точки зору, за образним висловом Еріка Белла, «результатом усього цього конфлікту було те, що вперті британці практично не просунулися в математиці протягом цілого століття після смерті Ньютона, в той час як прогресивніші швейцарці й французи, розвиваючи ідеї Лейбніца й користуючись його незрівнянно зручнішим способом позначень в аналізі, вдосконалили аналіз і зробили його простим, легко застосовним засобом досліджень, зробили те, що мали б були зробити безпосередні послідовники Ньютона».

Примітки

Коментарі

Джерела та використана література

Література

англійською мовою

• Bardi J. S. Calculus Wars: Newton, Leibniz, and the Greatest Mathematical Clash of All Time. — 2006. — 303 p. — ISBN 1-56025-706-7.
• Baron M. E. The origins of the infinitesimal calculus. — 1969. — 304 p. — ISBN 0-486-65371-4.
• Boyer C. B. The History of the Calculus and its conceptual development. — Dover Publications, inc, 1949. — 346 p.
• Gerhardt C. I. Leibniz in London // The Early Mathematical Manuscripts of Leibniz. — 1920. — С. 159—195.
• Feingold M. Newton, Leibniz, and Barrow Too: An Attempt at a Reinterpretation // Isis. — 1993. — Т. 84, № 2. — С. 310—338.
• Guicciardini N. Isaac Newton on Mathematical Certainty and Method. — The MIT Press, 2009. — 422 p. — ISBN 978-0-262-01317-8.
• Meli D. B. Equivalence and Priority: Newton versus Leibniz: Including Leibniz's Unpublished Manuscripts on the Principia. — Clarendon Press, 1993. — P. 318. — ISBN 0-19-850143-9.
• Hall A. R. Philosophers at War: The Quarrel between Newton and Leibniz. — Cambridge University Press, 1980. — P. 356. — ISBN 0 521 22732 1.
• Westfall R. S. Never at Rest. A Biography of Isaac Newton. — Cambridge University Press, 1980. — 908 p. — ISBN 978-0-521-23143-5.
• Whiteside T. The Mathematical Principles Underlying Newton's Principia Mathematica. — 1970. — 28 p. — ISBN 85261 014 9.

німецькою мовою

• Sonar T. Die Geschichte des Prioritätsstreits zwischen Leibniz and Newton: Geschichte – Kulturen – Menschen. — 2016. — 596 p. — ISBN 978-3-662-48862-1.

російською мовою

• Арнольд В. И. Гюйгенс и Барроу, Ньютон и Гук - Первые шаги математического анализа и теории катастроф. — М. : Наука, 1989. — 98 с. — ISBN 5-02-013935-1.
• Вавилов С. И. Исаак Ньютон. — 4-е, дополненное. — М. : Наука, 1989. — 271 с. — ISBN 5-02-000065-5.
• Герье В. И. Лейбниц и его век. — СПб. : Наука, 2008. — 807 с. — ISBN 978-5-02-026942-2.
• Карцев В. П. Ньютон. — М. : Молодая гвардия, 1987. — 416 с. — (ЖЗЛ)