Кривина (математика)
| Кривина | |
| Розмірність | |
|---|---|
| Формула | [1][2] |
| Позначення у формулі | і |
| Символ величини (LaTeX) | [1] |
| Підтримується Вікіпроєктом | Вікіпедія:Проєкт:Математика |
| Рекомендована одиниця вимірювання | обернений метрd[2][3] |
| | |
У диференціальній геометрії, кривина́ — збірна назва ряду кількісних характеристик (чисельних, векторних, тензорних), що описують відхилення того або іншого геометричного «об'єкта» (кривої, поверхні, ріманового простору тощо) від відповідних «пласких» об'єктів (пряма, площина, евклідів простір тощо).
Зазвичай кривина визначається для кожної точки на «об'єкті» і виражається як значення деякого диференціального виразу 2-го порядку. Іноді кривина визначається в інтегральному смислі, наприклад як міра, такі визначення використовують для «об'єктів» зниженої гладкості. Як правило, тотожне перетворення на нуль кривини в усіх точках означає збіг (локальний, але не глобальний) «об'єкта», що вивчається, з «пласким» об'єктом.
У цій статті наводяться тільки декілька простих прикладів визначень поняття кривини.
Кривина кривої[ред. | ред. код]
Нехай γ(s) — регулярна крива в d-вимірному евклідовому просторі, що параметризується довжиною. Тоді
називається кривиною кривої γ у точці p = γ(s), тут позначає другу похідну по s. Вектор
називається вектором кривини γ в точці p = γ(t0).
Нижче подані більш інтуїтивні визначення, що пояснюють геометричний зміст кривини.
Величина, обернена до кривини кривої (), називається радіусом кривини; він збігається з радіусом стичного кола в даній точці кривої. Центр цього кола називається центром кривини.
Кривина плоскої кривої[ред. | ред. код]
Нехай — плоска крива. Її кривина в деякій точці умовно кажучи, визначає наскільки крива в деякому малому околі цієї точки відхиляється від прямої. Для змістовності цієї числової характеристики кривина прямої мала б бути рівною нулю, а кривина в точках кола меншого радіуса мала б бути більшою, ніж у точках кола більшого радіуса. Тому кривину прямої можна визначити рівною нулю, а кривину кола радіуса r, як 1/r.
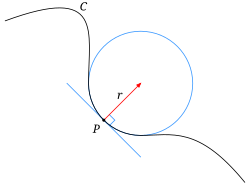
Тому якщо в деякому околі точки p крива досить добре наближається деяким колом (це коло називається стичним колом) радіуса r, то її кривину в точці p теж можна прийняти рівною 1/r. Стичне коло в точці визначається як границя кіл, що проходять через точки при
Нехай тепер для простоти крива параметризується довжиною і її перша та друга похідні по цьому параметру визначені й неперервні. Окрім того, є одиничним вектором тобто і де тут і надалі позначає скалярний добуток.
Якщо точки не лежать на одній прямій позначимо через — центр кола, що проходить через ці точки.
Тоді
З правил диференціювання скалярного добутку і теореми Ролля випливає існування таких чисел перше з яких знаходиться на проміжку між двома найменшими з чисел , а друге між двома найбільшими, що:
Повторно продиференціювавши й використавши теорему Ролля отримуємо існування числа для якого
Якщо тепер , то також і тому, якщо теж прямує до деякого , то попередні рівняння в граничному випадку мають вигляд:
Звідси очевидно, що така границя не може існувати, якщо Якщо ж , то можна довести, що жодні три точки в деякому околі точки не лежать на одній прямій і попередні побудови мають зміст. Також в цьому випадку з фінальних рівнянь однозначно визначається і з неперервності скалярного добутку випливає, що
Також з рівнянь випливає, що вектор який є радіус-вектором стичного кола є колінеарним до вектора Звідси маємо, що для радіуса r стичного кола виконується рівність , яку можна переписати як Тому саме можна визначати як кривину кривої в даній точці. У випадку кривина теж вважається нульовою.
Визначення плоскої кривої функцією кривини[ред. | ред. код]
Якщо — деяка неперервна функція, із невід'ємними значеннями то існує крива для якої кривина в точці є рівною
Окрім того, дві такі криві можуть бути отримані одна з іншої за допомогою перенесення та повороту площини.
Кривина у просторах вищої розмірності[ред. | ред. код]
Для кривих в Евклідових просторах розмірності > 2 попередня побудова теж має зміст при В цьому випадку довільні три точки в околі деякої точки теж не належать одній прямій. При прямуванні цих точок до в граничному випадку отримується площина визначена перпендикулярними векторами і В ній і буде лежати граничне коло побудоване як і раніше.
В цьому випадку, проте довільна неперервна функція не визначає криву . Для визначення кривої з точністю до ізометричних афінних відображень потрібні додаткові дані. Наприклад у випадку тривимірного простору також скрут кривої у кожній точці.
Визначення кривини як границі кутових функцій[ред. | ред. код]
Нехай знову ж деяка двічі неперервно диференційовна функція параметризована своєю довжиною. Кривину в точці можна також визначити в інший спосіб. Нехай — дотичні вектори в точках з відповідними параметрами. Для параметризації довжиною вони є одиничними. Позначимо — кут між цими векторами. Тоді кривина рівна границі відношення цього кута до довжини кривої між двома точками. Для параметризації довжиною це можна записати як:
Дійсно з елементарних властивостей трикутника справедлива рівність
Звідси маємо
При переході до границі, зважаючи на властивості синуса маємо
Формули для кривини в довільній параметризації[ред. | ред. код]
У формулі важливою є параметризація кривої її довжиною. Нехай тепер — довільна параметризація. Тоді є бієктивна функція яка для двічі неперервно диференційовних кривих теж є двічі неперервно диференційовною.
Позначаючи і похідні по відповідних параметрах маємо . Звідси і, як наслідок
Продиференціювавши останню рівність маємо:
Взявши абсолютні значення після подальших спрощень отримується формула:
де всі похідні є по параметру t.
Для плоских кривих записуючи в координатах формула кривини має вигляд:
Для кривих у тривимірному просторі кривину можна також записати як:
,
або в координатах
Кривина поверхні[ред. | ред. код]
Нехай — це регулярна поверхня у тривимірному евклідовому просторі. Хай — точка , — дотична площина до у точці , — одинична нормаль до у точці , а — площина, що проходить через і деякий одиничний вектор в . Крива , що виходить як перетин площини з поверхнею , називається нормальним перетином поверхні у точці у напрямі . Величина
де позначає скалярний добуток, а — вектор кривини у точці , називається нормальною кривиною поверхні у напрямі . З точністю до знаку нормальна кривина дорівнює кривині кривої .
У дотичній площині існують два перпендикулярні напрями і такі, що нормальну кривину в довільному напрямі можна представити за допомогою так званої формули Ейлера:
де — кут між і , a величини і нормальні кривини в напрямах і , вони називаються головними кривинами, а напрями і — головними напрямами поверхні в точці .
Головні кривини є екстремальними значеннями нормальних кривин.
Структуру нормальних кривин в даній точці поверхні зручно графічно зображати за допомогою індикатриси Дюпена.
Величина
- , (іноді )
називається середньою кривиною поверхні.
Величина
називається гаусовою кривиною поверхні. Гаусова кривина є об'єктом внутрішньої геометрії поверхонь, зокрема не змінюється при ізометричних вигинаннях.
Див. також[ред. | ред. код]
Література[ред. | ред. код]
- Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2023. — 1900+ с.(укр.)
- Погорелов А. И. Дифференциальная геометрия (6-е издание). [Архівовано 6 жовтня 2014 у Wayback Machine.] М.: Наука, 1974. [сторінка?]
- Рашевский П. К. Курс дифференциальной геометрии (3-е издание). [Архівовано 10 вересня 2011 у Wayback Machine.] М.-Л.: ГИТТЛ, 1950. [сторінка?]
- Spivak, Michael (1999), A comprehensive introduction to differential geometry, Volume II, Publish or Perish Press, ISBN 0-914098-71-3 [сторінка?]
Примітки[ред. | ред. код]
- ↑ а б 3-2 // Quantities and units—Part 3: Space and time — 1 — ISO, 2006. — 19 p.
- ↑ а б 3-2 // Quantities and units — Part 3: Space and time, Grandeurs et unités — Partie 3: Espace et temps — 2 — ISO, 2019. — 11 p.
- ↑ 3-2.a // Quantities and units—Part 3: Space and time — 1 — ISO, 2006. — 19 p.
Інтернет-ресурси[ред. | ред. код]
| Вікісховище має мультимедійні дані за темою: Кривина (математика) |
- The Feynman Lectures on Physics Vol. II Ch. 42: Curved Space
- The History of Curvature
- Curvature, Intrinsic and Extrinsic at MathPages
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Це незавершена стаття з математики. Ви можете допомогти проєкту, виправивши або дописавши її. |








![{\displaystyle \gamma (t):[a,b]\to \mathbb {R} ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1acdd38efd92647541955254f146313abbe1e40)
![{\displaystyle p=\gamma (t),\;t\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/105ca790db9da1295cd1e1fafca3b191f48be15c)
































![{\displaystyle \kappa :[0,L]\to \mathbb {R} ^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7de6b75687c974311f288cd1e24cfbb65b82a63f)
![{\displaystyle \gamma :[0,L]\to \mathbb {R} ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d9e80fc9af87acbc6fceeb67ad27fca242ce01b)
![{\displaystyle p=\gamma (s),s\in [0,L]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0daa9b05fda543b8ad8cdf55c804796279ef7ef)


![{\displaystyle \kappa :[0,L]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/faa99d97c91cbdf14cadde14dff5bd193ff24e59)
![{\displaystyle \gamma :[0,L]\to \mathbb {R} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2550b6197c4d49f16164149dd6dafc710626315)
![{\displaystyle \gamma (s),s\in [0,L]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb557aac48c6dd27ef9df87b8f87a1775fc2f79c)






![{\displaystyle \gamma (t):[a,b]\to \mathbb {R} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e19d641b4e58c8a5579eb6a4d42d7859109fa345)
![{\displaystyle s(t):[a,b]\to [0,L]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd2612eab71125922478a4fd3d57d922f299cc1d)






























