Метод Ейлера

Диференціальні рівняння
Види рівнянь Звичайні З частинними похідними Лінійні Нелінійні Автономні Алгебраїчні Диференціально-алгебраїчні Інтегро-диференціальні Однорідні Рівняння в повних диференціалах Стохастичні З запізненням
Загальні теми Фазовий простір Інтегральна крива Теорема Пікара — Лінделефа Фазовий портрет Диференціальний оператор Визначник Вронського Стійкість Чисельне інтегрування Фундаментальна матриця
Методи розв'язання Метод характеристик Розділення змінних Знижування порядку Інтегрувальний множник Метод невизначених коефіцієнтів Метод варіації параметрів Метод Ейлера Метод Рунге — Кутти Метод Адамса Метод скінченних різниць Метод Кранка-Ніколсон Метод скінченних елементів Метод Гальоркіна Інтегральне перетворення Теорія збурень
Відомі рівняння Рівняння Лотки-Вольтерри Дивний атрактор Лоренца Рівняння Дуффінга Осцилятор Ван дер Поля Система Хенона-Гейлса Рівняння Ріккаті Хвильове рівняння Рівняння Лапласа Рівняння дифузії Рівняння Бюргерса Рівняння Нав'є — Стокса Рівняння Гамільтона — Якобі Рівняння Коші-Ейлера Рівняння Бернуллі Модель Годжкіна — Гакслі Схема Чуа Атрактор Рьослера Модель Курамото
Математики Ісаак Ньютон Ґотфрід Лейбніц Леонард Ейлер П'єр-Симон Лаплас Жозеф Ліувілль Жозеф-Луї Лагранж Анрі Пуанкаре Рудольф Ліпшиц Олександр Ляпунов Еміль Пікар Карл Рунге Джон Кранк

Ілюстрація методу Ейлера. Шукана крива синя, а її полігональне наближення червоне.

В чисельних методах методом Ейлера називають спосіб розв'язувати звичайні диференціальні рівняння з заданим початковим значенням. Це найбільш базовий вид чисельних методів інтегрування звичайних диференціальних рівнянь.

Неформальний геометричний опис

Розгляньмо задачу рисування графіка невідомої кривої, яка починається в даній точці і задовольняє дане диференціальне рівняння. Тут дифрівняння може розглядатись як формула для тангенса кута нахилу дотичної до кривої, що може бути обчисленим в кожній точці цієї кривої за координатами.

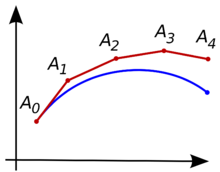
Ідея методу полягає в тому, що, хоча крива спочатку невідома, її початкова точка, яку ми позначимо $A_{0},$ відома (як на ілюстрації вгорі праворуч). Тоді, в цій точці можна обчислити нахил дотичної.

Тепер зробімо маленький крок вздовж дотичної до точки $A_{1}$. Якщо ми припустимо, що $A_{1}$ все ще на кривій (приблизно), тоді до неї можна застосувати ті ж міркування. Таким чином, ми отримаємо послідовність точок, що утворюють ламану, яка приблизно повторює криву.

Відхилення між отриманою ламаною можна зробити не надто великим, якщо робити короткі кроки вздовж дотичних і будувати криву на скінченному короткому інтервалі. Хоча для деяких рівнянь можуть виникати додаткові ускладнення.

Застосування

Ілюстрація чисельного інтегрування рівняння $y'=y,y(0)=1$. Синій - метод Ейлера, зелений - метод середньої точки, червоний - точний розв'язок, $y=e^{t}$. Розмір кроку - $h=1.0$.

Та ж ілюстрація для кроку $h=0.25$. Видно що метод середньої точки збігається швидше ніж метод Ейлера.

Ми хочемо наблизити розв'язок наступної задачі початкових значень:

$y'(t)=f(t,y(t)),\qquad \qquad y(t_{0})=y_{0},$

використовуючи перші два доданки ряду Тейлора для y, які представляють лінійне наближення біля точки $(t_{0},y(t_{0}))$. Один крок методу Ейлера з $t_{n}$ до $t_{n+1}=t_{n}+h$ проводиться так:

$y_{n+1}=y_{n}+hf(t_{n},y_{n}).\qquad \qquad$

Метод Ейлера є явним, тобто розв'язок $y_{n+1}$ є явною функцією $y_{i}$ для $i\leq n$.

Хоча метод Ейлера працює для ЗДР першого порядку, будь-яке ЗДР порядку $N$ може бути представленим як ЗДР першого порядку додаванням $N-1$ додаткових змінних, $y',\,y'',\,\ldots ,\,y^{(N)}$, і створенням $N$ рівнянь першого порядку з цими змінними. Метод Ейлера можна застосовувати до вектора $\mathbf {y} (t)=(y(t),y'(t),y''(t),...,y^{(N)}(t))$ для інтегрування системи рівнянь вищих порядків.

Похибка

Якщо припустити, що $f(t)$ і відповідно $y(t)$ відомі точно в момент $t_{0}$, тоді метод Ейлера дає приблизний розв'язок в момент $t_{0}+h$ як:

$y(t_{0}+h)=y(t_{0})+hf(t_{0},y(t_{0}))=y(t_{0})+hy'(t_{0})\,\qquad \qquad$

(друга рівність зберігається тому що y задовольняє дифрівняння $y'=f(t,y)$). Розклад Тейлора для $h$ біля $t_{0}$ дає:

$y(t_{0}+h)=y(t_{0})+hy'(t_{0})+{\frac {1}{2}}h^{2}y''(t_{0})+O(h^{3}).$

Похибка методу Ейлера задається різницею між цими двома рівняннями:

${\frac {1}{2}}h^{2}y''(t_{0})+O(h^{3}).$

Для маленьких $h$, домінуючий доданок похибки пропорційний $h^{2}$. Щоб розв'язати задачу на заданому проміжку $t$, необхідна кількість кроків, яка пропорційна до $1/h$ тому можна очікувати, що загальна похибка на кінці інтервалу буде пропорційна $h$ (похибка за один крок, помножена на кількість кроків). З цієї причини, метод Ейлера називають методом першого порядку, і він є менш точним (для малих $h$) ніж методи вищих порядків, таких як метод Рунге-Кутти, чи метод Адамса.

Стійкість

Метод Ейлера може бути чисельно нестійким, особливо для жорстких рівнянь. Це обмеження, поряд з тим фактом, що він повільно збігається при зменшенні $h$, означає, що метод використовується нечасто, і хіба що як простий приклад чисельного інтегрування. Нестійкості можна уникнути, використовуючи алгоритм Ейлера-Кромера.

Див. також

• Метод Рунге-Кутти
• Метод Адамса

Посилання

• Ascher, Uri M.; Petzold, Linda Ruth. Computer methods for ordinary differential equations and differential-algebraic equations. 1998. SIAM. ISBN 0898714125