Коефіцієнт асиметрії

Приклад експериментальних даних з ненульовою асиметрією.

Коефіцієнт асиметрії (англ. skewness) — числова характеристика розподілу ймовірностей дійсної випадкової величини.

Визначення

Асиметрією $\gamma _{1}$ (коефіцієнт асиметрії Фішера) теоретичного розподілу ймовірностей випадкової величини називають відношення центрального моменту третього порядку $\mu _{3}$ до куба середнього квадратичного відхилення $\sigma ^{3}$:

$\gamma _{1}=\mu _{3}/\sigma ^{3}\,.$

Аналогічно визначається оцінка асиметрії для емпіричного розподілу:

$\gamma _{1}=m_{3}/\sigma _{B}^{3}\,,$

де $m_{3}$ — центральний емпіричний момент третього порядку.

Додаткові визначення

Коефіцієнт асиметрії Пірсона

$\beta _{1}=\left({\frac {\mu _{3}}{\sigma ^{3}}}\right)^{2}=\gamma _{1}^{2}.$

Асиметрія моментів

$\alpha ^{(m)}\equiv {\frac {1}{2}}\gamma _{1}.$

Модальна асиметрія Пірсона

${\frac {[\mathrm {CePeDHE} ]-[\mathrm {MoDa} ]}{\sigma }}$

Властивості

Крива ліворуч має від'ємну асиметрію, а крива праворуч — додатню.

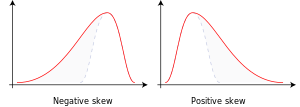
Асиметрія додатна, якщо «довша частина» розподілу знаходиться праворуч від математичного сподівання; асиметрія від'ємна, якщо «довша частина» кривої знаходиться ліворуч від математичного сподівання.

На практиці, знак асиметрії визначають за положенням кривої відносно моди: якщо «довша» частина кривої знаходиться правіше моди, то асиметрія додатня, якщо лівіше — від'ємна.

Див. також

• Коефіцієнт ексцесу

Джерела

• Карташов М. В. Імовірність, процеси, статистика. — Київ : ВПЦ Київський університет, 2007. — 504 с.
• Гнєденко Б. В. Курс теорії ймовірностей. — Київ : ВПЦ Київський університет, 2010. — 464 с.
• Гихман И. И., Скороход А. В., Ядренко М. В. Теория вероятностей и математическая статистика. — Київ : Вища школа, 1988. — 436 с.(рос.)
• Шефтель З. Г. Теорія ймовірностей. — 2-е. — Київ : Вища школа, 1994. — 192 с.(укр.)
• Сеньо П. С. (2007). Теорія ймовірностей та математична статистика (вид. 2-ге.). Київ: Знання. с. 556.