Квадрат

У Вікіпедії є статті про інші значення цього терміна: Квадрат (значення).

Квадрат
Правильний чотирикутник (тетрагон)
Вид	правильний многокутник
Ребра і вершини	4
Символ Шлефлі	{4}
Діаграма Коксетера
Група симетрії	діедральна (D4), порядок 2×4
Внутрішній кут (градуси)	90°
Властивості	опуклий, вписується в коло, рівносторонній, ізогональний, ізотоксальний

Квадра́т — чотирикутник, у якого всі сторони рівні і всі кути прямі. Для побудови квадрата необхідно і достатньо задати дві точки на координатній площині, які відповідатимуть будь-яким двом кутам і врахувати їхню суміжність.

Квадрат є водночас ромбом та прямокутником і навпаки: кожна фігура, яка є водночас ромбом і прямокутником, є квадратом.

Формули, пов'язані з квадратом

• Чорний колір — квадрат,
• Блакитний колір: описане коло;
• Коричневий колір: вписане коло

Якщо $a$ — довжина сторони квадрата, тоді

• Площа квадрата: $S=a^{2}$
• Довжина діагоналі: $d=a{\sqrt {2}}$
• Радіус вписаного кола: $r={\frac {a}{2}}$
• Радіус описаного кола: $R={\frac {\sqrt {2}}{2}}a$
• Периметр квадрата: $P=4a=4{\sqrt {2}}R=8r$

Властивості

• У квадрат завжди можна вписати коло;
• Навколо квадрата завжди можна описати коло.

Як і в будь-якого опуклого чотирикутника, в квадрата:

• Сума всіх внутрішніх кутів дорівнює 2π (360°).

Як і в будь-якому прямокутнику:

• Протилежні сторони паралельні.
• Діагоналі діляться точкою перетину навпіл.
• Точка перетину діагоналей є центром симетрії квадрата.
• Діагоналі рівні між собою.

Як і в будь-якому ромбі:

• Діагоналі є бісектрисами кутів.
• Діагоналі перетинаються під прямим кутом.
• Діагоналі є осями симетрії.

Побудова

Побудова квадрата за допомогою циркуля та лінійки

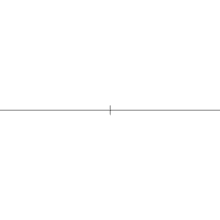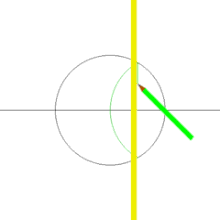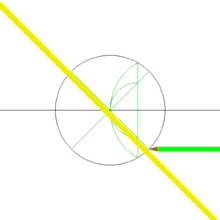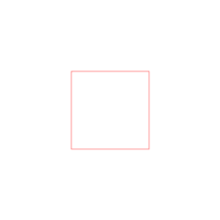
Квадрат можна побудувати за допомогою циркуля та лінійки за схемою, зображеною праворуч. Можна також побудувати дві перпендикулярні прямі, провести коло з центром у точці перетину прямих — чотири точки перетину прямих і кола будуть вершинами цього квадрата.

Див. також

• Ромб
• Прямокутник
• Куб
• Гіперкуб
• Магічний квадрат
• Квадратура круга
• Квадрування квадрата
• Гіпотеза Тепліца