Гомоморфізм
В алгебрі гомоморфізм — це зберігаюче структуру відображення[en] між двома алгебричними структурами того ж самого типу (наприклад, двома групами, двома кільцями, двома векторами просторами).
Слово гомоморфізм у перекладі з давньогрецької грец. homos – однаковий і грец. morphe – форма, вид.[1] Цей термін з'явився ще в 1892, його припусували німецькому математику Феліксу Клейну (1849—1925).[2]
Гомоморфізми двох векторних просторів також називають лінійними відображеннями, а їх дослідженнями займається лінійна алгебра.
Поняття гомоморфізму було узагальнено під назвою морфізм для багатьох структур, що не мають множини-носія або не є алгебраїчними. Це узагальнення — відправна точка теорії категорій
Гомоморфізм може також бути ізоморфізмом, ендоморфізмом, автоморфізмом і т.п. (дивись нижче). Кожен з цих гомоморфізмів може бути визначений способом, який можна узагальнити до будь-якого класу морфізмів.
Означення[ред. | ред. код]
Гомоморфізм — це відображення між двома алгебричними структурами одного типу (з однаковими назвами), що зберігає операції цих структур. Це означає відображення між двома множинами , , які мають однакові структуру такі, що якщо — операція цієї структури (для спрощення вважаємо її бінарною операцією), тоді
для будь-якої пари елементів , множини .[note 1] Часто говорять, що гомоморфізм зберігає операцію або сумісний з операцією.
Формально, відображення зберігає операцію арності , яка визначена на обох множинах, якщо
- ,
для всіх елементів множини .
Операції, що повинні зберігатися при гомоморфізмі, включають 0-арні операції, тобто константи. Зокрема, коли нейтральний елемент вимагається типом структури, то нейтральний елемент першої структури має відображатися в відповідний нейтральний елемент другої структури.
Наприклад,
- Гомоморфізм напівгруп — це відображення між напівгрупами, що зберігає операції напівгруп.
- Гомоморфізм моноїдів[en] — це відображення між моноїдами, що зберігає операції моноїдів та відображає нейтральний елемент першого моноїду у нейтральний елемент другого моноїду (нейтральний елемент це 0-арна операція).
- Гомоморфізм груп — це відображення між двома групами, що зберігає операції груп.
З цього випливає, що гомоморфізм груп відображає нейтральний елемент першої групи у нейтральний елемент другої групи, та відображає обернений елемент першої групи у обернений образ цього елемента. Тому, гомоморфізм напівгруп між групами обов'язково є гомоморфізмом груп.
- Гомоморфізм кілець — це відображення між кільцями, що зберігає додавання в кільцях, множення в кільцях та мультиплікативні тотожності.
- Лінійне відображення — це гомоморфізм векторних просторів, тобто гомоморфізм груп між векторними просторами, що зберігає структури абелевих груп та множення на скаляр.
- Гомоморфізм модулів[en], також називають лінійним відображення між модулями, визначають аналогічним чином.
- Гомоморфізм алгебр[en] — це відображення, що зберігає операції алгебри.
Алгебраїчна структура може мати більше однієї операція та гомоморфізм повинен зберігати кожну операцію. Таким чином, відображення, що зберігає тільки деякі операції не є гомоморфізмом структури, але лише гомоморфізмом субструктури, що отримується при розгляді лише збережених операцій. Наприклад, відображення між моноїдами, що зберігає операцію моноїда, а не нейтральний елемент, не є гомоморфізмом моноїду, але є гомоморфізмом напівгрупи.
При гомоморфізмі між алгебричними структурами позначення операцій в них не обов'язково повинні збігатися. Наприклад, дійсні числа утворюють групу з операцією додавання, а додатні дійсні числа утворюють групу з операцією множення. Експонента
задовольняє співвідношення
та визначає гомоморфізм між цими двома групами. Більш того, це навіть ізоморфізм (дивись нижче), бо її обернена функція (натуральний логарифм) задовольняє співвідношення
і це також гомоморфізм між групами.
В термінах універсальної алгебри, це відображення[en] , алгебричної системи в алгебраїчну систему того ж типу, що зберігає алгебраїчну операцію:
для кожної -арної операції і .
Базові приклади[ред. | ред. код]
Дійсні числа є кільцем, що має додавання і множення. Множина всіх матриць також кільце над додаванням матриць і множенням матриць. Якщо ми визначимо функцію між цими кільцями так:
де дійсне число. Тоді — гомоморфізм кілець, бо зберігає і додавання:
і множення:
Інший приклад, ненульові комплексні числа утворюють групу над множенням, так само як ненульові дійсні числа. (Нуль треба виключити, бо він не має оберненого елемента, який повинен бути в елементів групи.) Визначимо функцію з ненульових комплексних чисел в ненульові дійсні числа так
Де, — абсолютне значення (або модуль) комплексного числа . Тоді — гомоморфізм групи, бо воно зберігає множення:
Зауважте, що не можна поширити на гомоморфізм груп (з комплексних в дійсні), бо вона не зберігає додавання:
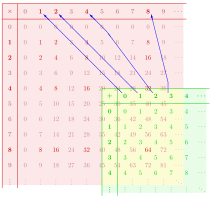
Як приклад на діаграмі показано гомоморфізм моноїду від моноїду до моноїду . Завдяки різним назвам відповідних операцій, властивості збереження структури, яким задовольняє $f$, запишуться як та .
Композиційна алгебра над полем має квадратичну форму, яка називається нормою, , яка є груповим гомоморфізмом з мультиплікативної групи[en] алгебри у мутиплікативну групу поля .
Типи гомоморфізмів[ред. | ред. код]
Кожен тип алгебричних структур має свій гомоморфізм:
- Гомоморфізм груп
- Гомоморфізм кілець
- Гомоморфізм модулів
- Лінійний оператор (гомоморфізм векторних просторів)
- Гомоморфізм алгебр
Часткові випадки[ред. | ред. код]
Декілька видів гомоморфізму мають спеціальні назви, які також визначаються для загальних морфізмов.
Ізомормізм[ред. | ред. код]
Ізоморфізм — бієктивний гомоморфізм.[3] [4] Ізоморфізм між алгебричними структурами одного типу зазвичай визначають як бієктивний гомоморфізм.
У більш загальному контексті теорії категорій ізоморфізм визначається як морфізм, який має обернене відображення, яке також є морфізмом. У випадку алгебраїчних структур ці два означення є еквівалентними, хоча вони можуть відрізнятися для неалгебраїчних структур, які мають множину-носія.
- Точніше, якщо
є (гомо)морфізмом, то він має обернений, якщо існує гомоморфізм
такий, що
Якщо та мають множини-носії та має обернене відображення , тоді є бієктивним. Дійсно, є ін'єктивним, оскільки з випливає, що , та є сюр'єктивним, так як для будь-якого з маємо, що , і є образом елемента з .
Навпаки, якщо — бієктивний гомоморфізм між алгебраїчними структурами, нехай — таке відображення, щоб єдиний елемент з такий, що . Маємо, що та , і залишається лише показати, що є гомоморфізмом. Якщо є бінарною операцією структури, то для будь-якої пари , елементів з маємо:
і, таким чином, сумісний з операцією . Оскільки доведення аналогічне для будь-якої арності, то це означає, що — гомоморфізм.
Це доведення не працює для неалгебраїчних структур. Наприклад, для топологічних просторів морфізм є неперервним відображенням, а обернене до бієктивного неперервного відображення не обов'язково є неперервним. Ізоморфізм топологічних просторів, який називається гомеоморфізмом або бінеперервним відображенням, таким чином, є бієктивним неперервним відображенням, обернене до якого також є неперервним.
Ендоморфізм[ред. | ред. код]
Ендоморфізм — гомоморфізм алгебраїчної категорії самої в себе. Ендоморфізм — це гомоморфізм, область визначення якого збігається з кообластю[en], або, в більш загальному сенсі, морфізм, джерело якого дорівнює цілі.[3]
Ендоморфізми алгебричної структури або об'єкта категорії утворюють моноїд за композицією.
Ендоморфізми векторного простору або модуля утворюють кільце. У випадку векторного простору або вільного модуля скінченної розмірності, вибір базису індикує ізоморфізм кільця між кільцем ендоморфізмів і кільцем квадратних матриць тієї ж розмірності.
Автоморфізм[ред. | ред. код]
Автоморфізм — ендоморфізм, що є одночасно ізоморфізмом.[3] Автоморфізми алгебричної структури або об'єкта категорії утворюють групу за композицією, яка називається групою автоморфізмів структури.
Багато іменних груп є групами автоморфізмів деякої алгебричної структури. Наприклад, загальна лінійна група — група автоморфізмів векторного простору розмірності над полем .
Групи автоморфізмів полів були введені Еваристом Галуа при дослідженні коренів многочленів і є основою теорії Галуа.
Мономорфізм[ред. | ред. код]
Мономорфізм — ін'єктивний гомоморфізм.[3] [4] У загальному контексті теорії категорій мономорфізм визначається як морфізм, який є лівим скороченням.[5] Це означає, що (гомо)морфізм є мономорфізмом, якщо для будь-якої пари морфізмів , з будь-якого іншого об'єкта в , з випливає, що .
Ці два означення мономорфізму еквівалентні для всіх загальних алгебраїчних структур. Точніше, вони еквівалентні для полів, для яких будь-який гомоморфізм є мономорфізмом, і для многовидів універсальної алгебри, тобто алгебраїчних структур, для яких операції і аксіоми (тотожності) визначаються без будь-яких обмежень (поля не утворюють многовидів, так як мультиплікативні обернені визначаються або як унітарна операція, або як властивість множення, які в обох випадках визначаються тільки для ненульових елементів).
Зокрема, два означення мономорфізму еквівалентні для множин, магм, напівгруп, моноїдів, груп, кільць, полів, векторних просторів і модулів.
Розщеплений мономорфізм[en] — це гомоморфізм, який має лівий обернений, і, таким чином, сам є правим оберненим цього іншого гомоморфізму. Тобто гомоморфізм є розщепленим мономорфізмом, якщо існує гомоморфізм такий, що . Розщеплений мономорфізм завжди є мономорфізмом для обох значень мономорфізму. Для множин і векторних просторів будь-який мономорфізм є розщепленим мономорфізмом, але ця властивість не виконується для більш загальних алгебраїчних структур.
Епіморфізм[ред. | ред. код]
Епіморфізм — сюр'єктивний гомоморфізм. В алгебрі епіморфізми часто визначаються як сюр'єктивні гомоморфізми.[3][4] З іншого боку, в теорії категорій епіморфізми визначаються як скоротні справа морфізми[5]. Це означає, що (гомо)морфізм є епіморфізмом, якщо для будь-якої пари , морфізмів з до будь-якого іншого об'єкта , рівність означає .
Сюр'єктивний гомоморфізм завжди є скоротним справа, але ця домовленість не завжди вірна для алгебраїчних структур. Однак, два визначення епіморфізму тотожні для множин, векторних просторів, абелевих груп, модулів (див. нижче для доведення) і груп. Важливість цих структур у всій математиці, і особливо в лінійній алгебрі та гомологічній алгебрі, може пояснити співіснування двох нетотожних визначень.
Алгебраїчні структури, для яких існують несюр'єктивні епіморфізми, включають напівгрупи і кільця. Основним прикладом є те що цілі числа входять до раціональних чисел, що є гомоморфізмом кілець і мультиплікативних напівгруп. Для обох структур це мономорфізм і не сюр'єктивний епіморфізм, але не ізоморфізм.[5][6]
Широким узагальненням цього прикладу є локалізація кільця мультиплікативною множиною. Кожна локалізація — це кільцевий епіморфізм, який, в загальному випадку, не сюр'єктивний. Оскільки локалізації є фундаментальними в комутативній алгебрі та алгебричній геометрії, це може пояснити, чому в цих областях визначення епіморфізмів як скоротних справа гомоморфізмів, як правило, є кращим.
Розділений епіморфізм[en] — це гомоморфізм, що має праве обернення і, таким чином, сам по собі є лівим оберненням від цього іншого гомоморфізму. Тобто гомоморфізм є розділеним епіморфізмом, якщо існує гомоморфізм такий, що Розділений епіморфізм завжди є епіморфізмом для обох значень епіморфізму. Для множин та векторних просторів, будь-який епіморфізм це розділений епіморфізм, та ця властивість не буде виконуватися для всіх алгебраїчних структур.
У підсумку, маємо
- розділений епіморфізм епіморфізм(сюр'єктивний) епіморфізм (скоротний справа)
останнє значення - еквівалентність множин, векторних просторів, модулів і абелевих груп; перше значення - еквівалентність множин і векторних просторів.
Ядро та образ гомоморфізму[ред. | ред. код]
- Гомоморфізм визначає відношення еквівалентності в так:
Відношення називається ядром .
- Фактор-множина ізоморфна образу .
Властивості[ред. | ред. код]
- Множина всіх ендоморфізмів множини утворює моноїд, позначається .
- Множина всіх автоморфізмів множини утворює групу, позначається .
Практичне значення[ред. | ред. код]
Поняття гомоморфізму і споріднені з ним поняття ізоморфізму і автоморфізму мають величезне практичне значення, так як вони дозволяють представляти одну модель іншою моделлю.
Див. також[ред. | ред. код]
Примітки[ред. | ред. код]
- ↑ Fricke, Robert (1897–1912). Vorlesungen über die Theorie der automorphen Functionen. B.G. Teubner. OCLC 29857037.
- ↑ Див.:
- Ritter, Ernst (1892). Die eindeutigen automorphen Formen vom Geschlecht Null, eine Revision und Erweiterung der Poincaré'schen Sätze [The unique automorphic forms of genus zero, a revision and extension of Poincaré's theorem]. Mathematische Annalen (нім.). 41: 1—82. doi:10.1007/BF01443449. S2CID 121524108. From footnote on p. 22: "Ich will nach einem Vorschlage von Hrn. Prof. Klein statt der umständlichen und nicht immer ausreichenden Bezeichnungen: "holoedrisch, bezw. hemiedrisch u.s.w. isomorph" die Benennung "isomorph" auf den Fall des holoedrischen Isomorphismus zweier Gruppen einschränken, sonst aber von "Homomorphismus" sprechen, … " (Following a suggestion of Prof. Klein, instead of the cumbersome and not always satisfactory designations "holohedric, or hemihedric, etc. isomorphic", I will limit the denomination "isomorphic" to the case of a holohedric isomorphism of two groups; otherwise, however, [I will] speak of a "homomorphism", …)
- Fricke, Robert (1892). Ueber den arithmetischen Charakter der zu den Verzweigungen (2,3,7) und (2,4,7) gehörenden Dreiecksfunctionen [On the arithmetic character of the triangle functions belonging to the branch points (2,3,7) and (2,4,7)]. Mathematische Annalen (нім.). 41: 443—468. doi:10.1007/BF01443421. S2CID 120022176. From p. 466: "Hierdurch ist, wie man sofort überblickt, eine homomorphe*) Beziehung der Gruppe Γ(63) auf die Gruppe der mod. n incongruenten Substitutionen mit rationalen ganzen Coefficienten der Determinante 1 begründet." (Thus, as one immediately sees, a homomorphic relation of the group Γ(63) is based on the group of modulo n incongruent substitutions with rational whole coefficients of the determinant 1.) From footnote on p. 466: "*) Im Anschluss an einen von Hrn. Klein bei seinen neueren Vorlesungen eingeführten Brauch schreibe ich an Stelle der bisherigen Bezeichnung "meroedrischer Isomorphismus" die sinngemässere "Homomorphismus"." (Following a usage that has been introduced by Mr. Klein during his more recent lectures, I write in place of the earlier designation "merohedral isomorphism" the more logical "homomorphism".)
- ↑ а б в г д Birkhoff, Garrett (1967), Lattice theory, American Mathematical Society Colloquium Publications, т. 25 (вид. 3rd), Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-1025-5, MR 0598630
- ↑ а б в Mac Lane, Saunders (1971). Categories for the Working Mathematician. Graduate Texts in Mathematics. Т. 5. Springer-Verlag. Exercise 4 in section I.5. ISBN 0-387-90036-5. Zbl 0232.18001.
- ↑ Dăscălescu, Sorin; Năstăsescu, Constantin; Raianu, Șerban (2001). Hopf Algebra: An Introduction. Pure and Applied Mathematics. Т. 235. New York, NY: Marcel Dekker. с. 363. ISBN 0824704819. Zbl 0962.16026.
Нотатки[ред. | ред. код]
- ↑ Як це часто буває, але не завжди, тут використовуються однакові символи для операції для обох множин та .
Цитування[ред. | ред. код]
Література[ред. | ред. код]
Українською[ред. | ред. код]
- (укр.) Гаврилків В. М. Елементи теорії груп та теорії кілець. — І.-Ф. : Голіней, 2023. — 153 с.
Іншими мовами[ред. | ред. код]
- Кон П. Универсальная алгебра. — Москва : Мир, 1968. — 351 с.(рос.)


































































