Логістичний розподіл

Логістичний розподіл
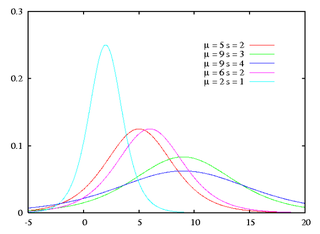Функція розподілу ймовірностей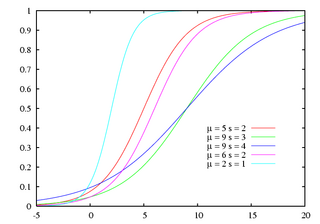
Параметри	$\mu \,$ $s>0\,$
Носій функції	$x\in (-\infty ;+\infty )\!$
Розподіл імовірностей	${\frac {e^{-(x-\mu )/s}}{s\left(1+e^{-(x-\mu )/s}\right)^{2}}}\!$
Функція розподілу ймовірностей (cdf)	${\frac {1}{1+e^{-(x-\mu )/s}}}\!$
Середнє	$\mu \,$
Медіана	$\mu \,$
Мода	$\mu \,$
Дисперсія	${\frac {\pi ^{2}}{3}}s^{2}\!$
Коефіцієнт асиметрії	$0\,$
Коефіцієнт ексцесу	$6/5\,$
Ентропія	$\ln(s)+2\,$
Твірна функція моментів (mgf)	$e^{\mu \,t}\,\mathrm {B} (1-s\,t,\;1+s\,t)\!$ для $|s\,t|<1\!$, Бета-функція
Характеристична функція	$e^{i\mu t}\,\mathrm {B} (1-ist,\;1+ist)\,$ для $|ist|<1\,$

Логістичний розподіл — неперервний ймовірнісний розподіл. Логістичний розподіл за формою нагадує нормальний розподіл, проте має більший коефіцієнт ексцесу.

Визначення розподілу

Функція щільності розподілу

Функція щільності (pdf) логістичного розподілу визначається за формулою:

$f(x;\mu ,s)={\frac {e^{-(x-\mu )/s}}{s\left(1+e^{-(x-\mu )/s}\right)^{2}}}\!$

$={\frac {1}{4\,s}}\;\operatorname {sech} ^{2}\!\left({\frac {x-\mu }{2\,s}}\right).$

Альтернативно визначивши підстановку $\sigma ^{2}=\pi ^{2}\,s^{2}/3$ одержується функція щільності:

$g(x;\mu ,\sigma )=f(x;\mu ,\sigma {\sqrt {3}}/\pi )={\frac {\pi }{\sigma \,4{\sqrt {3}}}}\,\operatorname {sech} ^{2}\!\left({\frac {\pi }{2{\sqrt {3}}}}\,{\frac {x-\mu }{\sigma }}\right).$

Функція розподілу

Функцією розподілу логістичного розподілу є логістична функція:

$F(x;\mu ,s)={\frac {1}{1+e^{-(x-\mu )/s}}}\!$

$={\frac {1}{2}}+{\frac {1}{2}}\;\operatorname {tanh} \!\left({\frac {x-\mu }{2\,s}}\right).$

Моменти розподілу

Математичне сподівання

$E[X]=\int _{-\infty }^{\infty }{\frac {xe^{-(x-\mu )/s}}{s\left(1+e^{-(x-\mu )/s}\right)^{2}}}\!dx=\int _{-\infty }^{\infty }{\frac {x}{4\,s}}\;\operatorname {sech} ^{2}\!\left({\frac {x-\mu }{2\,s}}\right)dx$

Підставимо: $u={\frac {(x-\mu )}{2s}},du={\frac {1}{2s}}dx$

$E[X]=\int _{-\infty }^{\infty }{\frac {2\,s\,u+\mu }{2}}\;\operatorname {sech} ^{2}\!\left(u\right)du$

$E[X]=s\int _{-\infty }^{\infty }u\;\operatorname {sech} ^{2}\!\left(u\right)du+{\frac {\mu }{2}}\int _{-\infty }^{\infty }\;\operatorname {sech} ^{2}\!\left(u\right)du$

Справедлива рівність: $\int _{-\infty }^{\infty }u\;\operatorname {sech} ^{2}\!\left(u\right)du=0$

$E[X]={\frac {\mu }{2}}\int _{-\infty }^{\infty }\;\operatorname {sech} ^{2}\!\left(u\right)du={\frac {\mu }{2}}\,2=\mu$

Моменти вищих порядків

Центральний момент n-го порядку може бути обчислений:

${\begin{aligned}\operatorname {E} [(X-\mu )^{n}]&=\int _{-\infty }^{\infty }(x-\mu )^{n}dF(x)=\int _{0}^{1}{\big (}F^{-1}(p)-\mu {\big )}^{n}dp\\&=s^{n}\int _{0}^{1}{\Big [}\ln \!{\Big (}{\frac {p}{1-p}}{\Big )}{\Big ]}^{n}\,dp.\end{aligned}}$

Інтеграл може бути виражений через числа Бернуллі:

$\operatorname {E} [(X-\mu )^{n}]=s^{n}\pi ^{n}(2^{n}-2)\cdot |B_{n}|.$

Див. також

• Нормальний розподіл

Література

• N., Balakrishnan (1992). Handbook of the Logistic Distribution. Marcel Dekker, New York. ISBN 0-8247-8587-8.
• Johnson, N. L., Kotz, S., Balakrishnan N. (1995). Continuous Univariate Distributions. Vol. 2 (2nd Ed. ed.). ISBN 0-471-58494-0.