Експоненційний розподіл

Показниковий розподіл

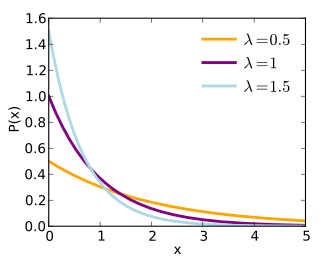Функція розподілу ймовірностей
Параметри	$\lambda > 0 \,$ - інтенсивність або зворотність коефіцієнт масштабу
Носій функції	$x \in [0;\infty)\!$
Розподіл ймовірностей	$\lambda e^{-\lambda x}\,$
Функція розподілу ймовірностей (cdf)	$1 - e^{-\lambda x}\,$
Середнє	$\lambda^{-1}\,$
Медіана	$\ln(2)/\lambda\,$
Мода	$0\,$
Дисперсія	$\lambda^{-2}\,$
Коефіцієнт асиметрії	$2\,$
Коефіцієнт ексцесу	$6\,$
Ентропія	$1 - \ln(\lambda)\,$
Твірна функція моментів (mgf)	$\left(1 - \frac{t}{\lambda}\right)^{-1}\,$
Характеристична функція	$\left(1 - \frac{it}{\lambda}\right)^{-1}\,$

Показниковий розподіл — абсолютно неперервний розподіл, що моделює час між двома послідовними завершеннями однієї і тієї ж події.

Визначення

Випадкова величина $X$ має експоненційний розподіл з параметром $\lambda > 0$, якщо її густина має вигляд

$f_X(x) = \left\{\begin{matrix} \lambda \,e^{-\lambda x} &,\; x \ge 0, \\ 0 &,\; x < 0. \end{matrix}\right.$.

Часто можна бачити експоненційний розподіл зі зсувом(параметр зсуву $x_0$)

$f_X(x) = \left\{\begin{matrix} \lambda \,e^{-\lambda (x - x_0)} &,\; x \ge x_0, \\ 0 &,\; x < x_0. \end{matrix}\right.$.

Інколи сімейство експоненційних розподілів параметризують зворотнім параметром $1/\lambda$:

$f_X(x) = \left\{\begin{matrix} {1 \over \lambda} \,e^{-{ (x-x_0) \over \lambda}} &,\; x \ge x_0, \\ 0 &,\; x < x_0. \end{matrix}\right.$.

Обидва способи однаково природні, і необхідна лише домовленість, який з них використовується.

Приклад. Хай є магазин, в який час від часу заходять покупці. При визначенних допущеннях, час між появами двох послідовних покупців буде випадковою величиною з експоненціальним розподілом. Середній час очікування нового покупця (див. нижчий) рівний $1/\lambda$. Сам параметр $\lambda$ тоді може бути інтерпретований як середнє число нових покупців за одиницю часу.

У цій статті, для визначеності, передбачатимемо, що щільність експоненціальної випадкової величини $X$ задана першим рівнянням, і писатимемо: $X \sim \mathrm{Exp}(\lambda)$.

Функція розподілу

Інтегруючи щільність, отримаємо функцію експоненційного розподілу: $F_X(x) = \left\{\begin{matrix} 1-e^{-\lambda x}&,\; x \ge 0, \\ 0 &,\; x < 0. \end{matrix}\right.$

Моменти

За допомогою нескладного інтегрування знаходимо, що функція моментів для експоненційного розподілу має такий вигляд:

$\mathrm{M}_x(t)= \left(1 - {t \over \lambda}\right)^{-1}$,

звідки отримуємо всі моменти:

$\mathbb{E}\left[X^n\right] = \frac{n!}{\lambda^n}$.

$\mathbb{E}[X] = \frac{1}{\lambda}$,

$\mathrm{D}[X] = \frac{1}{\lambda^2}$.

Властивості

Квантилі

Квантильна функція (обернена функція розподілу) для експоненційного розподілу, $E(\lambda)$ записується:

$F^{-1}(p;\lambda) = \frac{-\ln(1-p)}{\lambda}, \!$

для $0\le p<1$. Отже, квантилі:

перший (25% процентиль) 

$\ln(4/3)/\lambda$

медіана 

$\ln(2)/\lambda$

третій (75% процентиль)

$\ln(4)/\lambda$

Розподіл мінімуму експоненційно розподілених випадкових величин

Нехай $X_1,\dots,X_n$ — незалежні випадкові величини розподілені за експоненційним розподілом з параметрами $\lambda_1,\dots,\lambda_n$. Тоді

$\min\{\,X_1,\dots,X_n\,\}$

також експоненційна випадкова величина з параметром

$\lambda = \lambda_1+\cdots+\lambda_n.\,$

В цьому можна переконатися розглянувши доповнювальну функцію розподілу:

$\begin{align} \Pr(\min\{\,X_1,\dots,X_n\,\} > x) & = \Pr\left(X_1 > x \text{,}\dots\text{,}X_n > x\right) \\ = \prod_{i=1}^n \Pr(X_i > x) & = \prod_{i=1}^n \exp(-x\lambda_i) = \exp\left(-x\sum_{i=1}^n \lambda_i\right). \end{align}$

Індекс змінної, що є мінімумом розподілений згідно з законом

$\Pr(X_k=\min\{\,X_1,\dots,X_n\,\})=\frac{\lambda_k}{\lambda_1+\cdots+\lambda_n}.$

Зауважте, що

$\max\{\,X_1,\dots,X_n\,\}$

не є експоненційно розподілена.

Інші властивості

Якщо розглядати порядкові статистики $\xi_{(1)}, \xi_{(2)}, ... \xi_{(n)}$, з експоненціальним розподілом генеральної сукупності $\xi\sim\mathrm{Exp}(1/\lambda,x_0)$, то випадкові величини $n\xi_{(1)}, (n-i+1)(\xi_{(i)}-\xi_{(i-1)}), i = 2..n$ є незалежними.^{[Джерело?]}

Експоненційний розподіл у статистиці

Розглянемо генеральну сукупність $\xi\sim\mathrm{Exp}(1/\lambda)$.

Статистика вигляду $\hat{\theta}(\xi_{1},\ldots, \xi_{n}) = \bar{\xi} = \frac{1}{n} \sum\limits_{i=1}^n \xi_{i}$ є незміщеною, конзистентною та ефективною оцінкою параметру $\lambda$ розподілу генеральної сукупності. Незміщеність є наслідком того, що вибіркове середнє є незміщеною оцінкою для математичного сподівання випадкової величини, розподіл якої має генеральна сукупність.

Конзистентність. Використаємо критерій конзистентності для незміщених точкових оцінок. $\mathrm{D}[\bar{\xi}] = \frac{1}{n^2}\mathrm{D}[\sum\limits_{i=1}^n \xi_{i}] =\frac{1}{n}\mathrm{D}[\xi] = \frac{\lambda^2}{n} \to 0,$ при $n \to \infty$. Або можна використати те, що вибіркове середнє є конзистентною оцінкою математичного сподівання.

Для перевірки ефективності запишемо функцію правдоподібності: $L(\lambda, x_1, \dots, x_n)=\prod\limits_{i=1}^n f_X(\lambda, x_i) = \frac{1}{\lambda^n}e^{-\frac{1}{\lambda} \sum\limits_{i=1}^n x_i}$. Звідси логарифмічна функція правдоподібності: $\ln L(\lambda, x_1, \dots, x_n) = -n \ln(\lambda)-\frac{1}{\lambda} \sum\limits_{i=1}^n x_i$

$\frac{\partial}{\partial \lambda} \ln L(\lambda, x_1, \dots, x_n) = -\frac{n}{\lambda} +\frac{1}{\lambda^2}\sum\limits_{i=1}^n x_i$. Переходимо до випадкової вибірки, маємо: $\frac{\partial}{\partial \lambda} \ln L(\lambda, \xi_{1}, \dots, \xi_{n}) = -\frac{n}{\lambda} +\frac{n}{\lambda^2}\bar{\xi} = \frac{n}{\lambda^2}(\bar{\xi}-\lambda)$. А так як вибіркове середнє - незміщена оцінка параметку $\lambda$, то за нерівністю Рао-Крамера для незміщених точкових оцінок отримуємо бажаний результат, тобто вибіркове середнє є ефективною оцінкою параметра $\lambda$.

Посилання

• Online calculator of Exponential Distribution (англ.)
• Козлов М.В., Прохоров А.В. Введение в математическую статистику. - М.:Изд-во МГУ, 1987. - 264 с.