Розподіл хі-квадрат
| Хі-квадрат | |
|---|---|
 | |
|
Функція розподілу ймовірностей 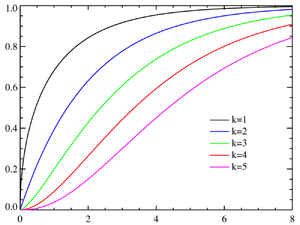 | |
| Параметри | — ступенів свободи |
| Носій функції | |
| Розподіл імовірностей | |
| Функція розподілу ймовірностей (cdf) | |
| Середнє | k |
| Медіана | |
| Мода | max{ k − 2, 0 } |
| Дисперсія | 2k |
| Коефіцієнт асиметрії | |
| Коефіцієнт ексцесу | 12 / k |
| Ентропія | |
| Твірна функція моментів (mgf) | (1 − 2 t)−k/2 for t < ½ |
| Характеристична функція | (1 − 2 i t)−k/2 [1] |
Розподіл хі-квадрат (χ²-розподіл) з 'n' ступенями вільності — неперервний розподіл, що визначається як розподіл суми квадратів 'n' незалежних випадкових величин з стандартним нормальним розподілом. Тобто якщо ξ1, ..., ξn — незалежні стандартні нормальні випадкові величини, то випадкова величина Xn2=ξ12+...+ξn2 матиме розподіл хі-квадрат з 'n' ступенями вільності.
Розподіл хі-квадрат є одним з найважливіших у статистиці. Зокрема він використовується у критеріях хі-квадрат (наприклад критерії узгодженості Пірсона).
Розподіл хі-квадрат є частковим випадком гамма-розподілу.
Вступ[ред. | ред. код]
Ланкастер[2] показав зв'язок між біноміальним, нормальним і хі-квадрат розподілами, як показано нижче. Де Муавр і Лаплас встановили, що біноміальний розподіл можна наблизити через нормальний розподіл. Точніше вони показали асимптотичну нормальність випадкової величини
де m — це спостережена кількість успіхів в N спробах, де ймовірність успіху p, а q = 1 − p.
Підносимо до квадрату обидві частини рівняння
Використовуючи N = Np + N(1 − p), N = m + (N − m), та q = 1 − p, це рівняння спрощується до
Вираз праворуч має форму, яку Пірсон узагальнив до:
де
- — кумулятивна тестова статистика Пірсона, яка асимптотично наближується до розподілу.
- — кількість спостережень типу i.
- — очікувана (теоретична) частота типу i, згідно з нульовою гіпотезою, яка стверджує, що частка типу i в популяції становить
- — кількість комірок в таблиці.
У випадку біноміального виходу (підкидання монети), біноміальний розподіл можна апроксимувати через нормальний (для досить великих n). З того, що квадрат нормального розподілу — це розподіл хі-квадрат з одним ступенем вільності, ймовірність результату як-от 1 аверс з 10 спроб, можна апроксимувати через нормальний розподіл чи розподіл хі-квадрат. Однак, багато задач потребують більше ніж два виходи як у біноміальному випадку, натомість вони потребують 3 або більше категорій, що призводить до поліноміального розподілу. Просто де Муавр і Лаплас шукали і знайшли нормальне наближення до біноміального, Пірсон шукав і знайшов багатовимірне нормальне наближення до поліноміального розподілу. Пірсон показав, що розподіл хі-квадрат, сума багатьох нормальних розподілів, був таким наближенням до поліноміального розподілу.[2]
Розподіл хі-квадрат[ред. | ред. код]
Щільність імовірності[ред. | ред. код]
Розподіл хі-квадрат зосереджений на додатній півосі і має щільність:
- ,
де — гамма-функція.
Функція розподілу[ред. | ред. код]
Функція розподілу хі-квадрат розподілу записується
При n>+2 χ2-розподіл має моду в точці x = n - 2. Характеристична функція χ2-розподілу має вигляд f(t)=(1-2it)-n/2.
Математичне сподівання і дисперсія розподілу хі-квадрат рівні, відповідно, n і 2n.
Властивості χ2-розподілу[ред. | ред. код]
- Розподіл хі-квадрат є стійким відносно додавання. Якщо Y1, Y2 незалежні, і , то
- З визначення легко отримати моменти розподілу хі-квадрат. Якщо то
- Через центральну граничну теорему, при великому числі ступенів вільності розподіл випадкової величини може бути наближений нормальним . Точніше по розподілу при .
Застосування[ред. | ред. код]
Сума незалежних випадкових величин Xn12+...+Xnk2 з n1, n2 ..., nk ступенями вільності, відповідно, підкоряється хі-квадрат розподілу з n = n1 + n2 + ... + nk ступенями вільності. Завдяки тісному зв'язку з нормальним розподілом χ2-розподіл відіграє важливу роль в теорії ймовірностей і математичній статистиці. χ2-розподіл, і багато інших розподілів, які визначаються за допомогою χ2-розподілу (наприклад — розподіл Стьюдента), описують вибіркові розподіли різних функцій від нормально розподілених результатів спостережень і використовуються для побудови довірчих інтервалів і статистичних критеріїв.
Так, наприклад, для незалежних випадкових величин x1, x2 ..., xn з однаковим нормальним розподілом з математичним сподіванням а і дисперсією δ2 відношення s2/δ2 ,
де ,
підкоряється χ2-розподілу з n - 1 ступенями вільності при будь-яких значеннях а і δ2. Цей результат покладений в основу побудови довірчих інтервалів і критерію для перевірки гіпотези про невідоме значення дисперсії у разі, коли середнє значення випадкової величини також невідоме (перевірка статистичних гіпотез і інтервальна статистична оцінка).
Особливу популярність у зв'язку з хі-квадрат розподілом отримав критерій хі-квадрат, заснований на так званій хі-квадрат статистиці Пірсона. Є детальні таблиці χ2-розподілу, зручні для статистичних розрахунків. При великих обсягах вибірок використовують апроксимацію за допомогою нормального розподілу. При , згідно з центральною граничною теоремою, розподіл нормальної величини прагне до нормального розподілу.
Вперше χ2-розподіл було розглянуто Р.Хельмертом (1876) і Карлом Пірсоном (1900).
Джерела[ред. | ред. код]
- Карташов М. В. Імовірність, процеси, статистика. — Київ : ВПЦ Київський університет, 2007. — 504 с.
- Гнеденко Б. В. Курс теории вероятностей. — 6-е изд. — Москва : Наука, 1988. — 446 с.(рос.)
- Гихман И. И., Скороход А. В., Ядренко М. В. Теория вероятностей и математическая статистика. — Київ : Вища школа, 1988. — 436 с.(рос.)
- William G. Cochran, Annals Math. Stat. 23 (1952), 315-345
Примітки[ред. | ред. код]
- ↑ M.A. Sanders. Characteristic function of the central chi-square distribution (PDF). Архів оригіналу (PDF) за 7 липня 2013. Процитовано 6 березня 2009.(англ.)
- ↑ а б Lancaster, H.O. (1969), The Chi-squared Distribution, Wiley
В іншому мовному розділі є повніша стаття Chi-square distribution(англ.). Ви можете допомогти, розширивши поточну статтю за допомогою перекладу з англійської. (серпень 2020)
|





















![{\displaystyle E[Y]=nD[Y]=2n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b301887e7712e47b92b583093c5c7721e33beded)




