Квантова електродинаміка
| Квантова теорія поля |
|---|
 |
| Історія |
|
Незавершені теорії |
|
Науковці |
Ква́нтова електродина́міка (КЕД) є релятивістською квантовою теорією електромагнітного поля. По своїй суті вона описує електромагнітну взаємодію, і є першою теорією, у якій досягнуто повного узгодження між квантовою механікою та спеціальною теорією відносності. КЕД математично описує взаємодію заряджених частинок через обмін квантами електромагнітного поля (фотонами) і є квантовим узагальненням класичної електродинаміки. Один із засновників КЕД Річард Фейнман назвав цю теорію «...дорогоцінним каменем фізики...» позаяк в її рамках було зроблено надзвичайно точні передбачення спостережуваних величин, таких, наприклад, як аномальний магнітний момент електрона та Лембівський зсув енергетичних рівнів атома водню.[1] Більш (спеціалізовано) технічно, КЕД може бути описана як теорія збурень електромагнітного квантованого вакууму.
Історія[ред. | ред. код]

Перше формулювання квантової теорії взаємодії випромінювання і матерії належить Полю Дираку, який у 1920 році обчислив коефіцієнти спонтанної емісії атома.[2] Дирак здійснив квантування електромагнітного поля, зобразивши його у вигляді ансамблю гармонічних осциляторів (фотонів) і увівши оператори їх породження і знищення. Згодом, завдяки доробкам таких учених як Вольфганг Паулі, Євген Вігнер, Паскуаль Джордан, Вернер Гейзенберг, тощо, та елегантному формулюванню квантової електродинаміки Енріко Фермі,[3] фізики прийшли до висновку, що в принципі можливо здійснювати обчислення будь-яких процесів за участю фотонів і заряджених частинок. Однак подальші дослідження Фелікса Блоха з Арнольдом Нордсьєком[4] і Віктора Вейскопфа[5] в 1937 і 1939 роках показали, що такі обчислення були достовірні лише для теорії збурень першого порядку, так як це передбачав Роберт Оппенгеймер.[6] При більших порядках виникали величини з безмежно великими значеннями, що робило такі обчислення безглуздими а саму теорію внутрішньо неузгодженою (суперечливою). Відсутність розв'язку цієї проблеми в той час привело до виникнення фундаментальної неузгодженості між спеціальною теорією відносності і квантовою механікою.

Труднощі із теорією зросли в кінці 1940 року. Удосконалення мікрохвильової технології зробило можливим значно покращити точність вимірів Лембівського зсуву спектральних ліній атома водню[7] та магнітного моменту електрона.[8] Експерименти виявили розбіжності, які теорія не могла пояснити. Перша вказівка на можливий вихід із становища належить Гансу Бете. В 1947 році, під час подорожі у потязі до Скенектаді із Нью-Йорка,[9] де Бете мав доповідь на конференції, він здійснив перше нерелятивістське обчислення зсуву спектральних ліній атома водню виміряне Лембом і Резерфордом.[10] Незважаючи на наближений характер обчислень узгодження виявилось чудовим. Ідея обчислень була простою і полягала в додаванні до фіксованих в експерименті значень заряду і маси безмежно великих величин. Завдяки цьому усі безмежності що виникали в теорії скорочувались а кінцевий результат обчислень був скінченним та дуже добре узгоджувався із експериментальними значеннями. Ця процедура обчислень була названа перенормуванням.

Базуючись на ідеї Бете та основних роботах на цю тему Томонаги,[11] Швінгера,[12][13] Фейнмана[14][15][16] і Дайсона[17][18] стало нарешті можливим отримати повністю коваріантне (читай релятивістське) формулювання, скінченне в обчисленнях при будь-якому порядку ряду теорії збурень квантової електродинаміки. Томонага, Швінгер і Фейнман одночасно були удостоєні в 1965 році Нобелівської премії за роботу в цій галузі.[19] Їх спільний внесок разом із Дайсоном до коваріантного калібрувально-інваріантного формулювання квантової електродинаміки дозволив здійснювати обчислення спостережуваних величин при різних порядках теорії збурень. Фейнманівський математичний метод, базований на його діаграмах, спочатку здавався дуже відмінним від теоретико-польового операторного підходу Швінгера і Томанаги, проте Дайсон пізніше показав що ці два підходи тотожні. Перенормування, що надає фізичного змісту безмежним величинам, які виникають в теорії через наявність розбіжних інтегралів, згодом стало одним з фундаментальних аспектів квантової теорії поля і вважається критерієм для загальної прийнятності теорії. Хоча перенормування дуже добре працює на практиці, Фейнман ніколи не був повністю задоволений його математичним обґрунтуванням, навіть жартівливо називав його "фокус-покус".[20] КЕД служить моделлю і шаблоном для всіх наступних теорій квантового поля. Одна з таких наступних теорій є квантова хромодинаміка, започаткована в 1960 році і приведена до завершеного вигляду в 1975 році Політзером, Колеманом, Гроссом і Вільчеком. На основі формалізму квантової електродинаміки Шелдон Ґлешоу, Стівен Вайнберг та Абдус Салам незалежно показали, як слабка та електромагнітна взаємодії можуть бути об’єднанні в одну електрослабку взаємодію.
Фейнманівське бачення квантової електродинаміки[ред. | ред. код]
Вступ[ред. | ред. код]
В останні роки свого життя Річард Фейнман прочитав серію науково-популярних лекцій про КЕД для широкого загалу. Ці лекції були записані і опубліковані під назвою «КЕД: Дивна теорія світла і матерії».[1][20] Ключовими компонентами Фейнманівської лекційної презентації присвяченої КЕД є три основні елементарні дії:
- Фотон рухається із однієї точки простору-часу у іншу точку простору-часу;
- Електрон рухається від однієї точки простору-часу до іншої точки простору-часу;
- Електрон випромінює або поглинає фотон у визначеній точці простору-часу;

Ці дії на фейнманівських діаграмах позначено простими символьними рисунками: хвилястою лінією позначено рух фотона, прямою - рух електрона, з’єднаними у вершині двома прямими і однією хвилястою лініями позначено випромінення або поглинання фотона електроном. Не слід надавати малюнкам якогось більшого значення. Вони не несуть жодної інформації про те, як частка потрапляє із однієї точки в іншу. Зокрема діаграми не позначають того, що частинки рухаються по прямій або кривій лінії. Вони також не позначають того, що частинка рухаються з фіксованою або змінною швидкістю. Той факт, що фотон прийнято зображати хвилястою лінією не означає, що він якось більше схожий на хвилю ніж електрон. Ці зображення є символьними і позначають лише зазначені вище дії: фотони і електрони якось рухаються від однієї точки до іншої, і електрони якимось чином випромінюють та поглинають фотони. Теорія не говорить нам про те, як ці події відбуваються, але вона говорить нам про ймовірність цих подій. Окрім зазначених рисунків, що зображають вказані елементарні дії, Фейнман запровадив також скорочення для числових величин, що позначають їхні ймовірності. Якщо фотон рухається із однієї точки простору-часу А до іншої точки простору-часу Б, то ймовірність такої події за Фейнманом слід позначати як Р(А до Б). Подібну ймовірність для руху електрона з С до Д позначено як Е(С до Д). Величину ймовірності випромінювання або поглинання фотона він позначив як 'j'. Це пов’язано, однак не зовсім те саме, що виміряний заряд електрона 'e'. КЕД базується на припущенні, що будь яку складну взаємодію великої кількості фотонів і електронів можна представити комбінацією трьох основних елементарних дій, а їх ймовірнісні величини дозволять обчислити імовірність складної взаємодії. Виявляється, що основну ідею КЕД можна спрощено пояснити в припущенні, що ймовірнісні величини, згадані вище, відповідають нашим повсякденним ймовірностям. Пізніше це пояснення можна скоректувати включенням спеціальної квантової математики згідно Фейнману.
Основні правила ймовірностей, які будуть використані, полягають у тому, що: а) якщо подія може відбутися в різний спосіб, то її ймовірність дорівнює сумі ймовірностей можливих шляхів її реалізації і б) якщо процес поділяється на низку незалежних підпроцесів, то ймовірність усього процесу є добутком ймовірностей підпроцесів.
Базові (основні) конструкції (діаграми)[ред. | ред. код]
Припустимо, що ми маємо один електрон в певній точці простору-часу (цю точку позначимо міткою А) і один фотон в іншій точці простору-часу (цю точку позначимо міткою B). Якою є ймовірність знаходження електрона в деякій обраній точці простору-часу C, а фотона в деякій іншій обраній точці простору-часу D? Самим простим способом досягнення цієї мети для електрона є безпосередньо перейти від А до С (елементарна дія), а для фотона безпосередньо перейти від В до D (інша елементарна дія). Згідно із правилом б) ймовірність реалізації обох процесів є добутком ймовірностей кожного з цих підпроцесів - Е (А до С) та Р (В до Д). Це проста відповідь на наше запитання.

Однак є і інші шляхи для досягнення заданої мети. Скажімо електрон може рухатись до точки простору-часу E, де поглине фотон що прийшов із точки B; далі електрон рухається до точки простору-часу F, де випромінює фотон; після цього новий фотон прямує до точки D, а електрон до точки C. Ймовірність такого складного процесу може бути обчислена на основі ймовірностей окремих елементарних дій: трьох елементарних переміщень електрона, двох елементарних переміщень фотона і двох вершин - одна позначає випромінення фотона, інша — поглинання. Згідно правила а), ця ймовірність (для будь яких фіксованих позицій E та F) є результатом множення ймовірностей усіх перерахованих елементарних дій. Далі, користуючись правилом б), ми повинні просумувати ймовірності розраховані для всіх можливих позицій E та F (на практиці це не є елементарно і передбачає інтегрування). Однак є і інша можливість: електрон рухається до точки G, де випромінює фотон який рухається до D; після цього, перш ніж потрапити до точки C, електрон рухається до точки простору-часу H, де він поглинає перший фотон. За аналогією до попереднього випадку, ми можемо обчислити сумарну ймовірність такого процесу. Додавши ймовірності цих двох можливих процесів до нашої початкової простої оцінки, ми отримаємо більш точне значення ймовірності для заданої події. Процес взаємодії фотона з електроном, який ми тут розглянули, має назву “розсіяння Комптона”. Існує нескінченне число інших більш складних проміжних процесів, в яких все більше і більше фотонів поглинається і/або випромінюється. При цьому кожну із цих можливостей можна зобразити за допомогою діаграм Фейнмана і знайти для неї ймовірність. За умови, коли збільшення складності процесів (збільшення кількості складових елементарних процесів) призводить до зменшення їх вкладу в сумарну ймовірність, отримання як завгодно точного результату для сумарної ймовірності є лише питанням часу і зусиль. Це є базовим підходом КЕД.
Для обчислення ймовірності будь-якого інтерактивного процесу між електронами і фотонами, необхідно перш за все описати його за допомогою діаграм Фейнмана, де всі можливі способи, в яких цей процес може бути реалізований, складатимуться із трьох основних елементів. Кожна діаграма передбачає здійснення деяких розрахунків за участю певних правил для знаходження відповідної ймовірності.
Така наглядна картина опису взаємодій світла і матерії загалом залишається справедливою і при переході до квантового формалізму, однак тут слід зробити деякі концептуальні зміни. Зокрема, всупереч очікуванням, що мають існувати обмеження на рух фотона і електрона в просторі-часі, в квантовій електродинаміці їх нема! З точки зору квантової електродинаміки існує можливість для електрона в A або фотона в B перейти в будь-яку іншу довільну точку простору-часу у Всесвіті. Це включає також точки, до яких частинкам прийдеться рухатись із швидкістю більшою за швидкість світла або зворотно в часі! (Електрон який рухається зворотно в часі можна розглядати як позитрон, що рухаються за часом.)
Амплітуда імовірності[ред. | ред. код]

Квантова механіка вносить суттєві зміни у розрахунок ймовірностей подій, які відбуваються за участю елементарних частинок. Замість ймовірностей, які є дійсними величинами, квантова механіка оперує амплітудами ймовірностей, які є комплексними величинами. При цьому зв’язок між ймовірністю P і її амплітудою w простий — ймовірність є квадратом амплітуди ймовірності: . Щоб не обтяжувати читача математикою комплексних чисел, Фейнман користується простим, але точним їх аналогом — зображає комплексні числа стрілками на аркуші паперу або екрані (не слід плутати зі стрілками діаграм Фейнмана, які, фактично, є спрощеним двомірним зображенням руху частинок в чотири-мірному просторі-часі.). Відтак операції додавання і множення, описані в правилах а) та б), згідно квантової механіки слід застосовувати до амплітуд ймовірностей (стрілок), а не до самих ймовірностей. Чому саме таку “математику” слід застосовувати для опису процесів на рівні елементарних частинок і атомів, залишається інтригуючою загадкою. Однак з прагматичної точки зору ми повинні прийняти той факт, що ця дивна арифметика, базована на амплітудах ймовірностей, є фундаментом для опису всіх квантових явищ.
Таким чином, ймовірність реалізації деякої події, у якій задіяні два процеси з амплітудами ймовірностей v і w, може бути обчислена за однією із формул:
або

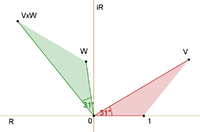
Операції додавання і множення комплексних чисел зображених стрілками приведені на малюнках. Сума знаходиться таким чином. Нехай початок другої стрілка буде в кінці першої. Їх сумою є третя стрілка, початок якої збігається з початком першої, а кінець — із кінцем другої. Добутком двох стрілок v і w, є стрілка, довжина якої є добутком довжин вихідних стрілок: , а напрямок знаходиться шляхом додавання кутів, на які повернуті вихідні стрілки v і w відносно деякого опорного напрямку.
Такий перехід від імовірностей до амплітуд імовірностей дещо ускладнює математику, однак не змінює основного підходу. Але цих змін не зовсім достатньо, оскільки вони не враховують той факт, що фотони і електрони можуть бути поляризовані, а отже їхні орієнтації в просторі та часі також треба брати до уваги. Отже, ймовірність поширення фотона від точки A до В, Р(A до В), насправді містить 16 комплексних чисел, або, що те саме, стрілок - амплітуд імовірностей. У зв’язку із цим можливі також деякі незначні зміни в розрахунку імовірності поглинання та/або емісії фотона 'j', які, однак, представляють інтерес тільки для детального бухгалтерського обліку.
Спираючись на той факт, що електрон може бути поляризованим, слід відмітити ще одну невелику проте важливу деталь, яка пов'язана з тим, що електрон є ферміоном і підпорядковується статистиці Фермі-Дірака. Додаткове правило полягає в тому, що якщо у нас є амплітуда ймовірності для заданого складного процесу, у якому задіяно більше одного електрона, то, коли ми включаємо (як ми завжди повинні) додаткову діаграму Фейнмана, у якій ми просто міняємо два електрони місцями, то амплітуда імовірності змінює свій знак на протилежний. Як приклад можемо розглянути два електрони в початкових позиціях А і В, які згодом потрапляють в С і D. Сумарна амплітуда буде розраховуватися як "різниця", E(A до D) × E(B до C) − E(A до C) × E(B до D), а не як сума, як це можна було б очікувати виходячи з нашого повсякденного досвіду.
Пропагатори[ред. | ред. код]
Щоб розрахувати величини P(A до B) і E (C до D), які відповідають амплітудам трансляції фотона і електрона відповідно, слід скористатись рівнянням Дірака, яке описує поведінку амплітуди ймовірності для електрона, і рівнянням Кляйна—Ґордона, яке описує поведінку амплітуди імовірності для фотона. Розв’язки цих рівнянь називаються пропагаторами Фейнмана. Перехід до позначень, які зазвичай використовуються в стандартній літературі, є таким:
де скорочений символ позначає чотири дійсні величини які задають положення точки A в просторі і часі.
Перенормування енергії (маси)[ред. | ред. код]

Хоча проблема виникла історично і розвивалась протягом двадцяти років, ми почнемо із зробленого припущення про існування трьох базових простих дій. Правила 'гри' говорять, що якщо ми хочемо розрахувати амплітуду імовірності трансляції електрона від точки A до B, ми мусимо врахувати усі можливі шляхи, якими це може статися. Зокрема ми повинні врахувати випадок, коли електрон спочатку подорожує до деякої точки C, випромінює фотон який, згодом, перш ніж потрапити в кінцеву точку B, поглинає в деякій іншій точці D. Такий проміжний процес випромінення-поглинання віртуального фотона може статися двічі, тричі, або більше разів. В результаті ми отримаємо фрактальну картину, в якій лінія при ретельному розгляді "розпадається" на колекцію простих ліній, кожна з яких, якщо дивитися ще уважніше, теж складається із простих ліній, і так далі до нескінченності.
Це дуже важка ситуація для реальних обчислень. Якщо б додавання таких процесів не суттєво вплинуло б на загальний результат, то нічого страшного б не сталося. Однак сталася біда - виявилось, що врахування таких процесів приводить до нескінченних значень амплітуд імовірностей. З часом ця проблема була "усунута" за допомогою техніки перенормування. Тим не менше, сам Фейнман залишилися незадоволеним таким способом втекти від проблеми, назвавши перенормування "Dippy process", що означає "беззмістовний процес". [20]
Висновки[ред. | ред. код]
В рамках КЕД вдалося обчислити з високим ступенем точності деякі з властивостей електронів, такі, як аномальний магнітний дипольний момент. Однак, як вказав Фейнман, в рамках КЕД не вдалося пояснити маси елементарних частинок таких як електрон. "Немає теорії, яка адекватно пояснює ці величини. Ми використовуємо ці величини у всіх наших теоріях, але ми їх не розуміємо - які вони є, або звідки вони беруться. Я вважаю, що з фундаментальної точки зору, це є дуже цікава і серйозна проблема."[21]
Математика[ред. | ред. код]
З математичної точки зору, КЕД є абелевою калібровочною теорією з групою симетрії U(1). Калібровочне поле, яке переносить взаємодію між зарядженими полями зі спіном 1/2, є електромагнітним полем. Лагранжіан КЕД для поля зі спіном 1/2, яке взаємодіє з електромагнітним полем, рівний дійсній частині виразу
де
- є матрицями Дірака;
- є амплітудою імовірності для біспінорного поля зі спіном 1/2 (тобто для електрон-позитронного поля);
- , має назву “псі-бар”, і є добутком ермітово спряженої хвильової функції на матрицю Дірака ;
- коваріантна похідна;
- e константа взаємодії, рівна заряду біспінорного поля;
- є коваріантним 4-потенціалом електромагнітного поля, що генерується електричним зарядом;
- є зовнішнім електромагнітним полем;
- є тензором електромагнітного поля.
Рівняння руху[ред. | ред. код]
Для початку, підставивши вираз D в лагранжіан, прийдемо до
Далі, ми можемо підставити цей лагранжіан до рівняння Ейлера-Лагранжа:
-
()
і знайти рівняння руху для поля. Як результат, два вирази із цього рівняння приймуть такий вигляд:
Підставляючи їх у рівняння Ейлера-Лагранжа ( 2) отримуємо, що
або, інакше, здійснивши комплексне спряження:
Переведення середнього члену до правої частини перетворює друге рівняння на
Ліва частина є рівнянням Дірака, тоді як права описує взаємодію із електромагнітним полем.
Ще одне важливе рівняння можна знайти, підставивши лагранжіан у інше рівняння Ейлера-Лагранжа, цього разу для поля, Aμ:
-
()
Два його вирази цього разу матимуть вигляд:
Підставляючи ці вирази назад до рівняння Ейлера-Лагранжа (3), отримаємо:
Тепер, якщо ми накладемо калібрувальну умову Лоренца, згідно якої дивергенція чотири-потенціалу має бути рівна нулю
отримаємо вираз
який являє собою хвильове рівняння для чотири-потенціалу, що збігається з класичним рівнянням Максвелла, записаним у калібруванні Лоренца.
Картина взаємодії[ред. | ред. код]
Ця теорія може бути безпосередньо квантованою в наближенні асимптотичної свободи бозонів (тобто фотонів та інших частинок з цілим спіном) та ферміонів (електронів, позитронів та інших частинок з напівцілим спіном). Це дозволяє побудувати безліч асимптотичних станів, які можуть бути використані як початкові наближення при обчисленні амплітуд ймовірностей для різних процесів. Для того щоб зробити це, нам потрібно обчислити оператор еволюції , що для заданого початкового стану , дасть кінцевий стан , таким чином, щоб отримати імовірність переходу
Ця техніка також відома як S-матриця. Оператор еволюції отримується в картині взаємодії, де час еволюції задається гамільтоніаном взаємодії, який рівний інтегралу другого члена лагранжіана (наведеного вище) по просторових координатах:
так, що для оператора еволюції матимемо
Цей оператор еволюції при обчисленнях слід розкладати в ряд за малим параметром, і те що ми отримаємо під час обчислень має вигляд ряду теорії збурень за сталою тонкої структури (яка є цим малим параметром). Цей ряд називається рядом Дайсона.
Діаграми Фейнмана[ред. | ред. код]
Незважаючи на концептуальну ясність такого підходу КЕД, майже жоден з ранніх підручників не слідував Фейнману у його поданні. При виконанні обчислень набагато легше працювати з Фур'є перетвореннями пропагаторів. Квантова фізика оперує здебільшого імпульсами частинок, а не їх позиціями, і досить зручно уявляти про частинки, що вони створюються або знищуються під час взаємодії. За таких обставин діаграми Фейнмана для різних частинок виглядають однаково, хоча лінії мають різні тлумачення. Лінія електрона (суцільна) позначає електрон із заданою енергією та імпульсом, лінія фотона (хвиляста), у свою чергу, позначає фотон із заданою енергією та імпульсом. Вершина представляє схему знищення одного електрона і створення іншого разом з поглинанням або випроміненням фотона, при цьому всі частинки мають певні (задані) енергії та імпульси.
Згідно теореми Віка для членів ряду Дайсона, всі елементи S-матриці для квантової електродинаміки можуть бути обчислені з використанням техніки базованої на діаграмах Фейнмана. У цьому випадку правила для малювання є такі
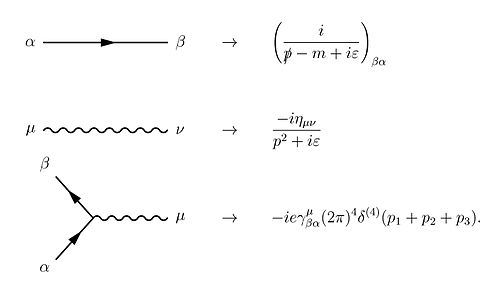
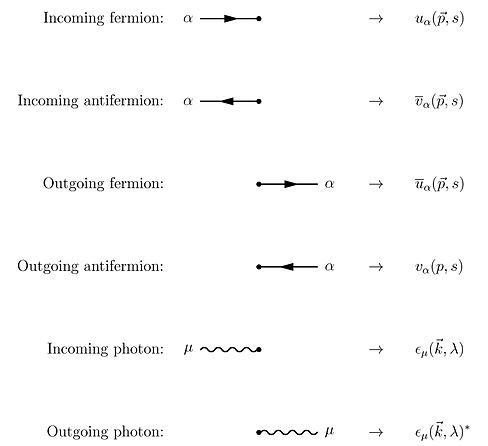
До цих правил ми повинні додати ще одне для замкнутих петель, яке містить інтегрування по імпульсах , оскільки внутрішні ("віртуальні") частинки не мають ніяких обмежень на значення енергії та імпульсу, навіть тих, які зазвичай потрібно накладати з огляду на спеціальну теорію відносності. Ці діаграми безпосередньо задають спосіб розрахунку амплітуди ймовірності для заданого процесу. Для прикладу можемо розглянути пружне розсіяння електрона і фотона. Діаграми Фейнмана в цьому випадку матимуть вигляд:

Таким чином, ми можемо доволі просто сконструювати вираз для амплітуди ймовірності цього процесу і використати його при розрахунку S-матриці в наближенні першого порядку теорії збурень:
за допомогою якої ми можемо розрахувати переріз взаємодії в такому процесі.
Перенормованість[ред. | ред. код]
Здавалося б, що члени вищого порядку можуть бути прямо обчислені для оператора еволюції, але ці члени зображуються діаграмами, що містять такі прості діаграми
-
Однопетлевий внесок до функції поляризації вакууму
-
Однопетлевий внесок до функції власної енергії електрона
-
Однопетлевий внесок до функції вершини
які, будучи замкнутими контурами, приводять до розбіжних інтегралів, що не мають математичного сенсу. Щоб подолати ці труднощі, була розроблена так звана техніка перенормування, яка приводить кінцеві результати розрахунків до дуже хорошої узгодженості із експериментом. Слід відзначити, що важливим критерієм теорії, який набув значення після запровадження техніки перенормування, є скінченність числа розбіжних діаграм. За таких умов теорія називається перенормованою. Це пов’язано із тим, що у цьому разі для здійснення перенормування потрібна скінченна кількість констант, і, як наслідок, передбачувана цінність теорії залишається недоторканою. КЕД є перенормованою теорією, оскільки у ній присутні лише три розбіжних діаграми. Процедура перенормування дозволяє робити передбачення, які знаходяться в дуже хорошому узгодженні із експериментом, як це видно на прикладі гіромагнітного співвідношення для електрона.
Перенормованість стала важливим критерієм для квантової теорії поля на її життєздатність. Всі теорії, які описують фундаментальні взаємодії, крім гравітації, квантова інтерпретація якої в даний час перебуває в стані активного дослідження, є перенормованими.
Розбіжність рядів КЕД[ред. | ред. код]
Фріман Дайсон показав, що радіус збіжності рядів КЕД за сталою взаємодії є рівним нулю. Його основний аргумент ґрунтується на тому, що негативне значення константи взаємодії є еквівалентним негативному значенню сталої кулонівської взаємодії. Тобто при зміні знаку константи взаємодії, кулонівська взаємодія також поміняє знак — однакові за знаком заряди будуть притягатися, а протилежні відштовхуватися. За таких обставин вакуум стане нестабільним — 'хмара' електронів попрямує до одного кінця Всесвіту, а 'хмара' позитронів до протилежного. Оскільки теорія є нестійкою до зміни знаку константи взаємодії при будь якому її абсолютному значенні, ряди КЕД за сталою взаємодії є розбіжними, однак при цьому вони є асимптотичними.
Див. також[ред. | ред. код]
Література[ред. | ред. код]
- ↑ а б Feynman, Richard (1985). Chapter 1. QED: The Strange Theory of Light and Matter. Princeton University Press. с. 6. ISBN 978-0-691-12575-6.
- ↑ P.A.M. Dirac (1927). The Quantum Theory of the Emission and Absorption of Radiation. Proceedings of the Royal Society of London A. 114 (767): 243—265. Bibcode:1927RSPSA.114..243D. doi:10.1098/rspa.1927.0039.
- ↑ E. Fermi (1932). Quantum Theory of Radiation. Reviews of Modern Physics. 4: 87—132. Bibcode:1932RvMP....4...87F. doi:10.1103/RevModPhys.4.87.
- ↑ F. Bloch; A. Nordsieck (1937). Note on the Radiation Field of the Electron. Physical Review. 52 (2): 54—59. Bibcode:1937PhRv...52...54B. doi:10.1103/PhysRev.52.54.
- ↑ V. F. Weisskopf (1939). On the Self-Energy and the Electromagnetic Field of the Electron. Physical Review. 56: 72—85. Bibcode:1939PhRv...56...72W. doi:10.1103/PhysRev.56.72.
- ↑ R. Oppenheimer (1930). Note on the Theory of the Interaction of Field and Matter. Physical Review. 35 (5): 461—477. Bibcode:1930PhRv...35..461O. doi:10.1103/PhysRev.35.461.
- ↑ W. E. Lamb; R. C. Retherford (1947). Fine Structure of the Hydrogen Atom by a Microwave Method,. Physical Review. 72 (3): 241—243. Bibcode:1947PhRv...72..241L. doi:10.1103/PhysRev.72.241.
- ↑ P. Kusch; H. M. Foley (1948). On the Intrinsic Moment of the Electron. Physical Review. 73 (3): 412. Bibcode:1948PhRv...73..412F. doi:10.1103/PhysRev.73.412.
- ↑ Schweber, Silvan (1994). Chapter 5. QED and the Men Who Did it: Dyson, Feynman, Schwinger, and Tomonaga. Princeton University Press. с. 230. ISBN 978-0-691-03327-3.
- ↑ H. Bethe (1947). The Electromagnetic Shift of Energy Levels. Physical Review. 72 (4): 339—341. Bibcode:1947PhRv...72..339B. doi:10.1103/PhysRev.72.339.
- ↑ S. Tomonaga (1946). On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields. Progress of Theoretical Physics. 1 (2): 27—42. doi:10.1143/PTP.1.27.
- ↑ J. Schwinger (1948). On Quantum-Electrodynamics and the Magnetic Moment of the Electron. Physical Review. 73 (4): 416—417. Bibcode:1948PhRv...73..416S. doi:10.1103/PhysRev.73.416.
- ↑ J. Schwinger (1948). Quantum Electrodynamics. I. A Covariant Formulation. Physical Review. 74 (10): 1439—1461. Bibcode:1948PhRv...74.1439S. doi:10.1103/PhysRev.74.1439.
- ↑ R. P. Feynman (1949). Space–Time Approach to Quantum Electrodynamics. Physical Review. 76 (6): 769—789. Bibcode:1949PhRv...76..769F. doi:10.1103/PhysRev.76.769.
- ↑ R. P. Feynman (1949). The Theory of Positrons. Physical Review. 76 (6): 749—759. Bibcode:1949PhRv...76..749F. doi:10.1103/PhysRev.76.749.
- ↑ R. P. Feynman (1950). Mathematical Formulation of the Quantum Theory of Electromagnetic Interaction. Physical Review. 80 (3): 440—457. Bibcode:1950PhRv...80..440F. doi:10.1103/PhysRev.80.440.
- ↑ F. Dyson (1949). The Radiation Theories of Tomonaga, Schwinger, and Feynman. Physical Review. 75 (3): 486—502. Bibcode:1949PhRv...75..486D. doi:10.1103/PhysRev.75.486.
- ↑ F. Dyson (1949). The S Matrix in Quantum Electrodynamics. Physical Review. 75 (11): 1736—1755. Bibcode:1949PhRv...75.1736D. doi:10.1103/PhysRev.75.1736.
- ↑ The Nobel Prize in Physics 1965. Nobel Foundation. Архів оригіналу за 26 Грудня 2018. Процитовано 9 жовтня 2008.
- ↑ а б в Feynman, Richard (1985). QED: The Strange Theory of Light and Matter. Princeton University Press. с. 128. ISBN 978-0-691-12575-6.
- ↑ Feynman, Richard (1985). QED: The Strange Theory of Light and Matter. Princeton University Press. с. 152. ISBN 978-0-691-12575-6.
Додаткова література[ред. | ред. код]
- Ребенко О. Л. Основи сучасної теорії взаємодіючих квантованих полів. — К. : Наукова думка, 2007. — 539 с.
- Ахиезер А. И., Берестецкий В. Б. Квантовая электродинамика. — М. : Наука, 1981. — 432 с.
- Ландау Л. Д., Лифшиц Е. М. Квантовая электродинамика // Теоретическая физика. — М. : Физматлит, 2006. — Т. 4. — 720 с.
- Тирринг В. Принципы квантовой электродинамики = Principles of Quantum Electrodynamics. — М. : Высшая школа, 1964. — 228 с.
- Фейнман Р. Квантовая электродинамика = Quantum Electrodynamics. — М. : Мир, 1964. — 220 с.
- Фейнман Р. КЭД — странная теория света и вещества = QED: The Strange Theory of Light and Matter. — М. : Наука, 1988. — 144 с.
Посилання[ред. | ред. код]
- Квантова електродинаміка [Архівовано 25 Жовтня 2020 у Wayback Machine.] //ЕСУ
- Пескін M., Шродер Д. Вступний курс квантової теорії поля. — T.1 (переклад з англійської) [Архівовано 10 Вересня 2015 у Wayback Machine.]
- Квантовая электродинамика [Архівовано 13 Червня 2013 у Wayback Machine.] // Физическая энциклопедия, т. 2. - М., Сов. энцикл.1990, с. 317—318

































![{\displaystyle U=T\exp \left[-{\frac {i}{\hbar }}\int _{t_{0}}^{t}dt'V(t')\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51293780be77a246b9f2123ab3f968bf749831ae)






