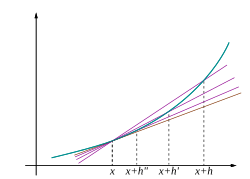Похідна
| Вибрані статті із |
| Числення |
|---|
|
|
|
Спеціалізоване |

Похідна́ (заст. витвірна́[1]) — основне поняття диференціального числення, що характеризує швидкість змінювання функції. Визначається як границя відношення приросту функції до приросту її аргументу, коли приріст аргументу прямує до нуля (якщо така границя існує). Функцію, що має скінченну похідну, називають диференційовною.
Процес знаходження похідної функції називається диференціюва́нням. Зворотним до диференціювання є інтегрування — процес знаходження первісної.
Означення похідної[ред. | ред. код]
Нехай в деякому околі точки x0 визначена функція ƒ. Якщо ми візьмемо довільне число x в цьому околі, то приріст аргументу (позначається Δx) в цьому випадку визначається, як x − x0, а приріст функції (Δy) — як ƒ(x) − ƒ(x0). Тоді, якщо існує границя , то вона називається похідною функції ƒ в точці x0.
Похідною функцією даної функції називається функція, що в будь-якій точці області визначення дорівнює похідній даної функції в цій точці.
Диференціювання та похідна[ред. | ред. код]

Диференціювання — це метод обчислення співвідношення приросту залежної змінної y по відношенню до приросту незалежної змінної x. Це співвідношення приростів називається похідною функції y по змінній x. Якщо говорити більш точно, залежність y від x означає, що y функція від x. Ця функціональна залежність часто позначається y = ƒ(x), де ƒ позначає функцію. Якщо x та y дійсні числа, і якщо графік функції y зображено відносно x, похідна дорівнює нахилу дотичної до цього графіка в кожній точці.
Найпростіший випадок коли y — лінійна функція від x, це означає що графік функції y відносно x пряма лінія. В такому випадку, y = ƒ(x) = mx + b, для дійсних чисел m та b, і нахил m визначається так
де символ Δ (грецька літера у верхньому регістрі дельта) — це є скорочення для «зміни в». Ця формула справедлива тому, що
- y + Δy = ƒ(x + Δx) = m(x + Δx) + b = mx + b + mΔx = y + mΔx.
З цього випливає, що Δy = mΔx.
Отримали точне значення нахилу прямої лінії. Якщо функція ƒ не лінійна (тобто графік функції не пряма лінія), тоді приріст y поділений на приріст x змінюється: диференціювання це спосіб обчислення точного значення відношення приростів для будь-якого значення x.
Ідея полягає в тому (див. малюнки 1—3), щоб обчислити відношення приростів як граничну величину Δy / Δx коли Δx стає нескінченно малим.
Якщо використати позначення Лейбніца, тоді нескінченно малий приріст x позначається як dx, а похідна функції y по змінній x записується:
виглядає як відношення двох нескінченно малих величин. (Цей вираз читається так: «похідна функції y по змінній x» або «де ігрек по де ікс».)
Пояснення визначення[ред. | ред. код]
Нехай ƒ — функція дійсних чисел. В класичній геометрії, дотична до графіка функції ƒ для дійсного числа a була єдина лінія через точку (a, ƒ(a)), що не перетинається з графіком функції ƒ трансверсально, це означає що ця лінія не проходить крізь графік. Похідна функції y по змінній x в точці a, з геометричної точки зору, це нахил дотичної лінії до графіка функції ƒ в точці a. Нахил дотичної дуже близький до нахилу лінії, що проходить крізь точку (a, ƒ(a)) та іншу близьку точку на графіку, наприклад (a + h, ƒ(a + h)). Такі лінії називаються січними. Значення h близьке до нуля дає добре наближення для нахилу дотичної, а чим менше значення h, в загальному випадку, тим краще буде наближення. Нахил m січної лінії дорівнює різниці значень y для цих точок поділити на різницю значень x, тобто
Цей вираз — це відношення приростів Ісаака Ньютона. Похідна — це значення відношення приростів у випадку коли січні лінії наближаються до дотичної. Щиро кажучи, похідна функції ƒ в точці a це границя:
відношення приростів коли h наближається до нуля, якщо така границя існує. Якщо границя існує тоді ƒ — диференційовна в точці a. Тут ƒ′(a) одне з кількох можливих позначень похідної (див. нижче)
Запишемо еквівалентний вираз, для похідної справедлива рівність
що також піддається інтуїтивному розумінню (див. рис. 1), де дотична лінія ƒ в точці a дає найкраще лінійне наближення
для ƒ біля точки a (наприклад, для малих h). Якщо підставити 0 замість h у відношення приростів то отримаємо ділення на нуль, отже нахил дотичної лінії не можна обчислити таким способом. Натомість запишемо Q(h), відношення приростів як функцію від h:
Q(h) — це нахил січної лінії між точками (a, ƒ(a)) та (a + h, ƒ(a + h)). Якщо ƒ — неперервна функція, тобто якщо графік функції не має розривів, тоді Q також неперервна функція починаючи з точки h = 0. Якщо існує границя , тобто якщо існує спосіб обчислити значення для Q(0), це означає що графік функції Q неперервний, тоді функція ƒ диференційовна в точці a, і її похідна в точці a дорівнює Q(0).
На практиці, існування неперервного продовження відношення приростів Q(h) в точці h = 0 показують по-іншому: міняють чисельник таким чином щоб скоротити h у знаменнику. Цей процес може бути довгим та нудним для складних функцій, тож в таких випадках використовують багато спрощень.
Приклад[ред. | ред. код]
Квадратна функція ƒ(x) = x2 — диференційовна в точці x = 3 і її похідна в цій точці дорівнює 6. Цього результату можна досягнути, якщо обчислити границю відношення приростів ƒ(3) при h прямує до нуля:
Тепер можемо обчислити границю, якщо підставимо замість h нуль:
Отже, нахил графіку квадратної функції в точці (3, 9) дорівнює 6, а її похідна в точці x = 3 дорівнює ƒ'(3) = 6. Узагальнюючи, якщо провести схожі обчислення то отримаємо, що квадратна функція в точці x = a дорівнює ƒ'(a) = 2a.
Неперервність і диференційованість[ред. | ред. код]
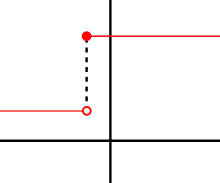
Якщо y = ƒ(x) — диференційовна в точці a, тоді ƒ також має бути неперервна в точці a. Для прикладу, виберемо точку a і нехай ƒ буде кроковою функцією, що дорівнює 1, для всіх x менших ніж a і дорівнює іншому значенню, скажімо 10, для всіх x, які більші або дорівнюють a. ƒ не має похідної в точці a. Якщо h — від'ємне, тоді a + h знаходиться на нижній сходинці функції, тоді січна лінія від a до a + h дуже круто піднімається вгору і якщо h прямує до нуля тоді нахил лінії прямує до нескінченності. Якщо h додатне, тоді a + h на верхній сходинці і січна лінія від a до a + h має нахил, що дорівнює нулю. Відповідно січні лінії не утворюють єдиний нахил, отже границя від відношення приростів не існує.

Проте якщо функція неперервна в точці, тоді вона не обов'язково диференційовна в цій точці. Наприклад, функція абсолютної величини y = |x| є неперервною в точці x = 0, але не є диференційовною в цій точці. Якщо h додатне, тоді нахил січної лінії від 0 до h дорівнює одиниці, якщо h від'ємне, тоді нахил січної лінії від 0 до h дорівнює −1. На графіку цю точку видно як «зубець» в точці x = 0. Навіть функції з графіком без «зубців» не є диференційовані в точці де дотична лінія є вертикальна: наприклад функція y = 3√x не є диференційовною в точці x = 0.
Підведемо підсумки: щоб отримати похідну від функції ƒ необхідна умова щоб функція ƒ була неперервною, але тільки цього не достатньо.
Більшість функцій, що зустрічаються на практиці мають похідні у всіх точках, або майже у всіх точках. Раніше на початку вивчення математичного аналізу, багато математиків припускали, що неперервна функція диференційовна в більшості точок. Для м'яких умов, наприклад якщо маємо монотонну функцію або Ліпшицеву функцію це формулювання справедливе. Проте в 1872 Веєрштрас знайшов перший приклад функції, яка неперервна усюди, але не є диференційованою в жодній точці. Ця функція відома як функція Веєрштраса. В 1931 році Стефан Банах довів, що множина функцій, які мають похідну хоча б в якійсь точці, є множиною першої категорії в просторі всіх неперервних функцій.[2]
Позначення[ред. | ред. код]
Похідна позначається як , що вимовляється «еф-штрих від ікс».
Функція, що має скінченну похідну в точці x, зветься диференційованою в точці x.
Похідна також позначається, як відношення диференціалів . У фізиці для позначення похідних по часу використовують крапку над змінною, наприклад .
Позначення Лейбніца[ред. | ред. код]
Позначення похідної запропоноване Лейбніцом було одним з найперших. Воно широко використовується дотепер. Якщо вираз y = ƒ(x) розглядається як функціональна залежність між залежною і незалежною змінними. Тоді перша похідна позначається як:
- , або
похідні вищого порядку позначаються таким чином
- , або
для похідної n-го порядку y = ƒ(x) (по змінній x). Це є скорочення для багаторазового застосування оператора похідної. Наприклад,
Через позначення Лейбніца ми можемо записати похідну функції y в точці x = a двома різними способами:
Позначення Лейбніца дає змогу вказувати змінну диференціювання (в знаменнику). Це особливо важливо для часткового диференціювання. В такому позначенні також легше запам'ятати ланцюгове правило:
Позначення Лагранжа[ред. | ред. код]
Позначення Лагранжа одне з найпоширеніших сучасних позначень для диференціювання, що вперше використав Жозеф-Луї Лагранж. Для позначення похідної використовують знак штрих, таким чином похідна функції ƒ(x) позначається ƒ′(x) чи просто ƒ′ подібним чином друга та третя похідна позначаються
- and
Починаючи звідси деякі автори застосовують римські цифри:
для четвертої похідної, тоді як інші автори ставлять цифру порядку похідної в дужки:
Останній запис узагальнює позначення ƒ(n) для похідної функції ƒ n-го порядку — таке позначення особливо зручне коли ми говоримо про похідну як про функцію, в цьому випадку застосування позначення Лейбніца може бути надто громіздким.
Позначення Ньютона[ред. | ред. код]
Позначення Ньютона для диференціювання, також називається точкове позначення, ставлять крапку над назвою функції для позначення похідної. Якщо y = ƒ(t), тоді
- і
означає відповідно першу та другу похідну функції y по змінній t. Таке позначення застосовується майже виключно для похідних за часом, тобто незалежна змінна функції є часом. Воно дуже поширене у фізиці і математичних дисциплінах пов'язаних з фізикою, наприклад диференціальні рівняння. Хоча таке позначення стає проблематичним у користуванні для похідних високого порядку, на практиці потрібні тільки кілька перших похідних.
Обчислення похідної[ред. | ред. код]
Похідну функції можна, теоретично, обчислювати використовуючи границю відношення приростів. На практиці, достатньо знати похідні обмеженої кількості простих функцій, тоді можна обчислити складніші випадки за допомогою правил диференціювання.
Похідні простих функцій[ред. | ред. код]
В більшості випадків для того щоб обчислити похідну потрібно знати похідні певних поширених функцій. Нижче наведено неповний перелік з похідних деяких найуживаніших функцій однієї дійсної змінної.
- Степенева функція: Якщо
- ,
де r — будь-яке дійсне число, то
- ,
для будь-яких випадків коли визначена функція. Наприклад, якщо r = 1/2, то
- .
Тут функція визначена тільки для додатних x. Якщо r = 0, це правило повторює правило константи.
Приклад знаходження похідної за визначенням[ред. | ред. код]
Нехай є функція y = c, де c — деяка константа. Тоді при будь-якому x0 та при будь-якому Δx зміна (приріст) функції дорівнюватиме нулю, отже і похідна такої функції дорівнюватиме нулю.
Похідні вищих (старших) порядків[ред. | ред. код]
Поняття похідної довільного порядку задається рекурентно:
- похідна нульового порядку — сама функція
- похідна n-го порядку для натурального n, що більше 0, — похідна похідної (n − 1)-го порядку
Іноді замість «похідна n-го порядку» говорять «n-а похідна».
Похідна n-го порядку функції ƒ зазвичай позначається як ƒ(n)(x)
- якщо n мале (1, 2, 3) — то використовується відповідна кількість рисок, ƒ′(x), ƒ′′(x), ƒ′′′(x), вимовляється як «еф-штрих від ікс»; про другу — «еф-два-штрихи від ікс».
- Можна зустріти історичне позначення похідної за допомогою римської системи числення (перша похідна: ƒ′(x), друга: ƒII(x), шістнадцята: ƒXVI(x)).
- В фізиці також зустрічається позначення похідної другого порядку по часу у вигляді двох крапок над змінною: .
Геометричний зміст похідної[ред. | ред. код]
Значення похідної функції у точці дорівнює значенню кутового коефіцієнта дотичної до кривої у точці з абсцисою .
Рівняння дотичної до кривої у точці має вигляд:
y = ƒ'(x) = tg a
Фізичний зміст похідної[ред. | ред. код]
Похідна від шляху за часом дорівнює миттєвій швидкості руху матеріальної точки. Похідна від миттєвої швидкості руху матеріальної точки дорівнює миттєвому прискоренню.
Див. також[ред. | ред. код]
Посилання[ред. | ред. код]
- Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2023. — 1900+ с.(укр.)
- Означення похідної // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 238. — 594 с.
- Похідні вищих порядків // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 256. — 594 с.
- В. Г. Болтянский, Что такое дифференцирование?, «Популярные лекции по математике», Выпуск 17, Гостехиздат 1955 г., 64 стр.
- FIZMA.neT - математика онлайн
Примітки[ред. | ред. код]
- ↑ Реєстр репресованих слів.
- ↑ Banach, S. (1931), Uber die Baire'sche Kategorie gewisser Funktionenmengen, Studia. Math. (3): 174—179.. Cited by Hewitt, E and Stromberg, K (1963), Real and abstract analysis, Springer-Verlag, Theorem 17.8
|