Напівправильний многогранник

|

|

|

|

|

|

|

|

|

|

|

|

|
Напівправильні многогранники — низка опуклих многогранників, які не є правильними[1], але мають деякі їхні ознаки, серед яких однаковість усіх граней, всі грані є правильними многокутниками, просторова симетрія. Визначення може диференціюватися включаючи різні види многогранників, та в першу чергу сюди відносять архімедові тіла.
Архімедові тіла[ред. | ред. код]
Архімедові тіла — опуклі многогранники, із двома властивостями:
- Всі грані є правильними многокутниками двох чи більше типів (якщо всі грані є правильними многокутниками одного типу, це — правильний многогранник);
- Для будь-якої пари вершин існує симетрія многогранника (рух що переводить многогранник в себе) що переводить одну вершину в іншу. Зокрема,
- Всі многогранні кути при вершинах конгруентні.
Історичні спогади приписують побудову перших напівправильних многогранників Архімеду, хоча доказових праць щодо обґрунтування ним принципів їх побудови не знайдено.
Каталанові тіла[ред. | ред. код]
Тіла, двоїсті архімедовим, так звані каталанові тіла, мають конгруентні грані (переводяться одна в одну зсувом, обертанням або відбиттям), рівні двогранні кути та правильні многогранні кути. Каталанові тіла теж іноді називають напівправильними многогранниками. У цьому випадку напівправильними многогранниками вважають сукупність архімедових і каталанових тіл. Архімедові тіла є напівправильними многогранниками в тому сенсі, що їхні грані – правильні многокутники, але вони не однакові, а каталанові – в тому сенсі, що їхні грані однакові, але не є правильними многокутниками; при цьому для тих і тих зберігається умова одного з типів просторової симетрії: тетраедричного, октаедричного або ікосаедричного.
Тобто, напівправильними в цьому випадку називають тіла, в яких відсутня тільки одна з перших двох із таких властивостей правильних тіл:
- усі грані є правильними многокутниками ;
- усі грані однакові;
- тіло належить до одного з трьох типів просторової симетрії.
В архімедових тіл відсутня друга властивість, у каталанових - перша, третю властивість мають тіла обох видів.
Існує 13 архімедових тіл, два з яких (кирпатий куб і кирпатий додекаедр) не є дзеркально-симетричними і мають ліву та праву форми. Відповідно, існує 13 каталанових тіл.
Список напівправильних многогранників[ред. | ред. код]
| Многогранник — архімедове тіло | Грані | Вершини | Ребра | Конфігурація вершини | Двоїстий — каталанове тіло | Група симетрії |
|---|---|---|---|---|---|---|
 Кубооктаедр |
8 трикутників 6 квадратів |
12 | 24 | 3,4,3,4 |  Ромбододекаедр |
Oh |
 Ікосододекаедр |
20 трикутників 12 п'ятикутників |
30 | 60 | 3,5,3,5 |  |
Ih |
 Зрізаний тетраедр |
4 трикутники 4 шестикутники |
12 | 18 | 3,6,6 |  |
Td |
 Зрізаний октаедр |
6 квадратів 8 шестикутників |
24 | 36 | 4,6,6 |  (заломлёний куб) |
Oh |
 Зрізаний ікосаедр |
12 п'ятикуттників 20 шестикутників |
60 | 90 | 5,6,6 |  |
Ih |
 Зрізаний куб |
8 трикутників 6 восьмикутників |
24 | 36 | 3,8,8 |  |
Oh |
 Зрізаний додекаедр |
20 трикутників 12 десятикутників |
60 | 90 | 3,10,10 |  |
Ih |
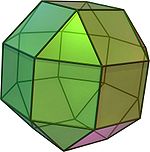 Ромбокубооктаедр |
8 трикутників 18 квадратів (6 — у кубічному положенні, 12 — у ромбічному) |
24 | 48 | 3,4,4,4 |  |
Oh |
 |
20 трикутників 30 квадратів 12 п'ятикутників |
60 | 120 | 3,4,5,4 |  |
Ih |
 |
12 квадратів 8 шестикутників 6 восьмикутників |
48 | 72 | 4,6,8 |  |
Oh |
 |
30 квадратів 20 шестикутників 12 десятикутників |
120 | 180 | 4,6,10 |  |
Ih |
  |
32 трикутники
|
24 | 60 | 3,3,3,3,4 | 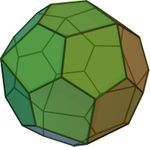  |
O |
  |
80 трикутників
|
60 | 150 | 3,3,3,3,5 |   |
I |
Інші[ред. | ред. код]
Крім архімедових і каталанових тіл, існують нескінченні послідовності многогранників, що належать до напівправильних: ті правильні призми та правильні антипризми, у яких усі ребра рівні.
Використання[ред. | ред. код]
Каталанові тіла - разом із платоновими тілами, рівногранними біпірамідами і трапецоедрами - використовують як гральні кісточки в деяких настільних іграх (див. світлини). Архімедові тіла, в яких грані не рівноправні і тому мають різні шанси випадання, для цього мало придатні.
Див. також[ред. | ред. код]
Примітки[ред. | ред. код]
- ↑ Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія 10-11 клас. — К. : Вежа, 2002. — С. 103. ISBN 966-7091-31-7.
Література[ред. | ред. код]
- Гордєєва Є. П., Величко В. Л. Нарисна геометрія. багатогранники (правильні, напівправильні та зірчасті). Частина І. Навчальний посібник. Луцьк: Редакційно-видавничий відділ ЛДТУ, 2007. — 198с.
Посилання[ред. | ред. код]
- Ашкинузе В. Г. О числе полуправильных многогранников // Математическое просвещение. Вторая серия. — 1957. — Вип. 1 (21 квітня). — С. 107-118.
- Залгаллер В. А. Выпуклые многогранники с правильными гранями// Записки научных семинаров ЛОМИ. Том 2 -- 1966.