Біротонда

Множина біротонд
Семисхила біротонда в прямій та повернутій формах (приклад)
Тип	Множина біротонд
Граней	6n+2: 2 правильних n-кутників, 2n п'ятикутників, 4n рівнобедрених трикутників.
Ребер	12n
Вершин	6n
Характеристика Ейлера	$\chi =\Gamma -{\hbox{P}}+{\hbox{B}}=2$
Група симетрії	Прямі: Dnh, [n,2], (*n22), порядок 4n (Симетрія n-Призми) Повернуті: Dnd, [2n,2+], (2*n), порядок 4n (Симетрія n-Антипризми)
Група поворотів	Dn, [n,2]+, (n22), порядок 2n
Дуальний многогранник	?
Властивості	Опуклий

Біротонда (n‒схила біротонда) — тіло, утворене поєднанням двох ротонд по їх нижній основі (правильній 2n-кутній грані).

Паралельні грані основ коаксікальні, тобто мають спільну вісь.

Існує дві форми n-схилих біротонд:

1. Пряма n-схила біротонда, утворюється при поєднанні ротонд в прямій орієнтації (поєднуються однойменні грані на бічних смугах ротонд). Ця форма утворюється при дзеркальному відображенні n-схилої ротонди відносно площини нижньої основи.
2. Повернута n-схила біротонда, утворюється при поєднанні ротонд в повернутій орієнтації (поєднуються різнойменні грані на бічних смугах ротонд). Ця форма утворюється, якщо одну з ротонд повернути на величину центрального кута нижнього 2n-кутника (а саме ${\frac {\pi }{n}}$ радіан) відносно іншої ротонди.

n-схилі біротонди за будовою споріднені з n-схилими бікуполами, з різницею в будові бічної смуги:

‒ в бікуполах чергуються прямокутники та рівнобедрені трикутники;

‒ в біротондах чергуються п'ятикутники (які мають щонайменше чотири рівних сторони) та пари рівнобедрених трикутників.

n-схила біротонда має вісь симетрії порядку n, що проходить через центри основ.

Ротонди і біротонди існують як нескінченні множини багатогранників, так само, як множини куполів, бікуполів, пірамід, біпірамід, призм , антипризм, трапецоедрів та ін.

Приклади

Родина біротонд

4	5	6	7	8
Чотирисхила пряма біротонда	П'ятисхила пряма біротонда	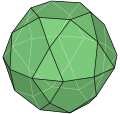Шестисхила пряма біротонда	Семисхила пряма біротонда	Восьмисхила пряма біротонда
Чотирисхила повернута біротонда	П'ятисхила повернута біротонда (Ікосододекаедр)	Шестисхила повернута біротонда	Семисхила повернута біротонда	Восьмисхила повернута біротонда

П'ятисхила біротонда може бути утворена рівносторонньою та правильногранною:

‒ п'ятисхила пряма біротонда є одним з багатогранників Джонсона (J₃₄);

‒ п'ятисхила повернута біротонда, більш відома як ікосододекаедр, є одним з напівправильних багатогранників Архімеда.

Див. також

Подовжена п'ятисхила пряма біротонда

Подовжена п'ятисхила повернута біротонда

Скручена подовжена п'ятисхила біротонда

Література

• Norman W. Johnson. Convex Solids with Regular Faces // Canadian Journal of Mathematics. — 1966. — Т. 18. — С. 169—200. — ISSN 0008-414X. — DOI:10.4153/CJM-1966-021-8. (Містить оригінальне перерахування 92 тіл і гіпотезу, що інших немає.)
• Залгаллер В. А. . Выпуклые многогранники с правильными гранями. — М.—Л. : Наука, 1967. — Т. 2. — 221 (_rusian) с. — (Зап. научн. сем. ЛОМИ) (Перший доказ, що існує тільки 92 тіл Джонсона.)
• Victor A. Zalgaller (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN.